线性回归笔记

线性回归

目的

        找到一个直线 /（超）平面，使预测值与真实值之间的误差最小化

预测函数

均方误差（Mean Squared Error，MSE）代价函数

我们要做的是

        找到一组(a1,a2,...,an)，使均方误差代价函数最小

求系数a的过程：

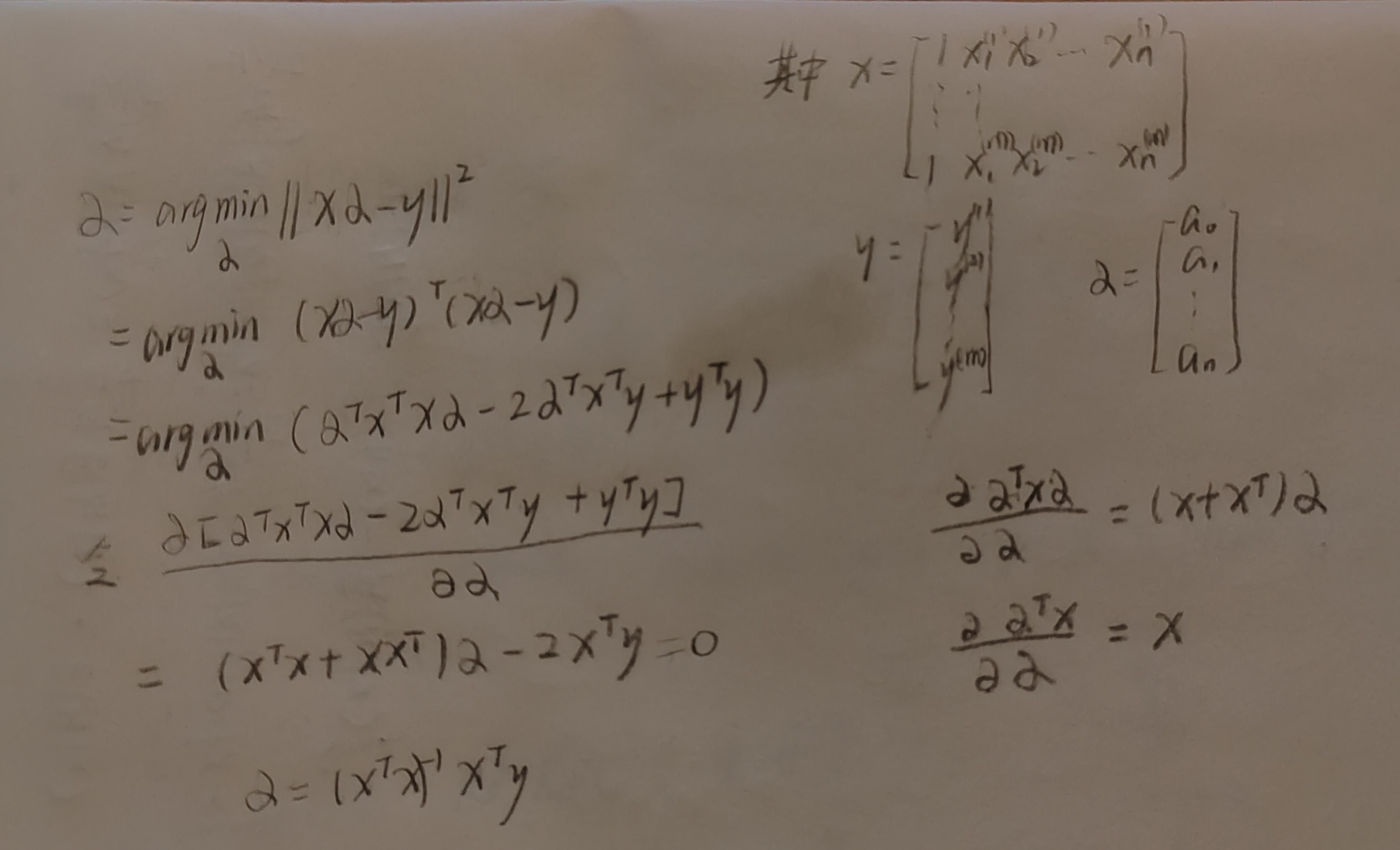
梯度下降优化

分类

BGD：每一次更新梯度都用到全部样本

SGD：每一次更新梯度只用到一个随机样本 

 

MBGD：每一次更新梯度用部分样本

 

α是学习率，它控制每次参数更新的步长。

参数更新公式推导

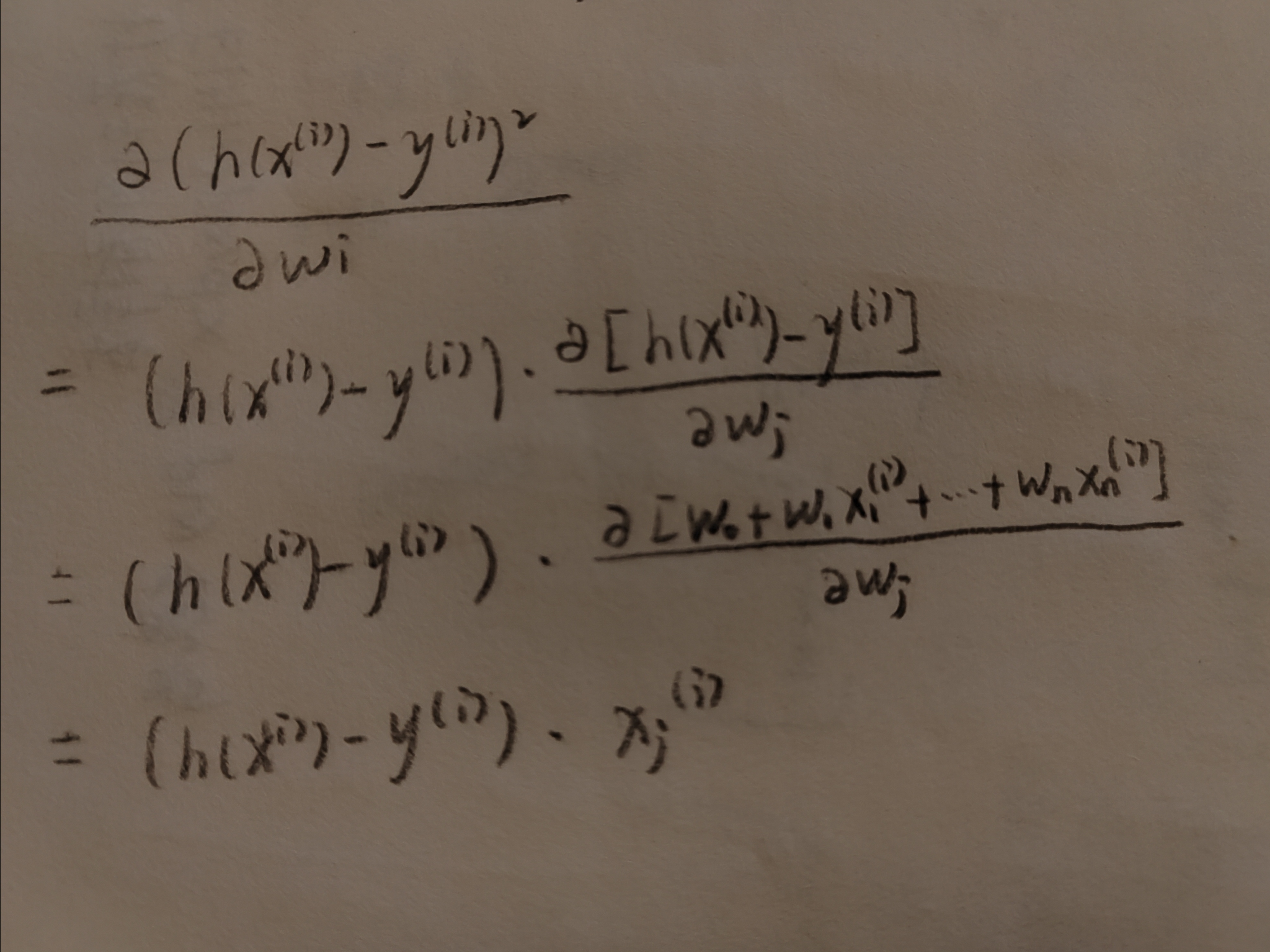
梯度下降vs最小二乘法

梯度下降

        优：当特征较多时也适用，适用于各种模型 。缺：需调学习率、迭代次数可能较多

最小二乘法

        优：不需设置学习率，一次性算出解析解。缺：特征数量较大（>1000）时代价大，只适用于线性回归，不适于逻辑回归（借助逻辑函数（Sigmoid 函数 ），将线性回归的输出映射到 0 和 1 之间，以此预测事件发生概率。）等。

归一化 / 标准化

原因

        ①加速模型收敛
        ② 提升模型精度（使不同尺度特征同尺度具备可比较性，使不同尺度特征对目标变量的影响处于同一数量级）

适用

        KNN、K - means、SVM、LR 一般需要归一化 / 标准化
        DT - RF、XGBoost、LightGBM、Naive Bayes 对特征取值尺度不敏感，一般无需归一化 / 标准化

正则化

        正则化（Regularization）是用于防止模型过拟合和提高泛化能力的重要技术。它通过在损失函数中添加额外的 “惩罚项”，对模型参数进行约束，避免模型学习到训练数据中的噪声或复杂模式。

过拟合处理

        ① 降低 model 复杂度② 收集更多 data ③ 使用 PCA 降维（减少特征个数）④ 正则化项⑤ 集成多个 model

欠拟合处理

        ① 提高model 复杂度② 添加新特征③ 降低正则化系数

L1 正则化（Lasso Regression）

        J(w)是代价函数；w是模型的参数向量；λ>0。

        加入后面那一项后，在最小化目标函数 J(w) 时，不仅要考虑减小训练误差（原代价函数 ），还要考虑让参数 w 的绝对值之和尽量小。

       为什么要让参数 w 的绝对值之和尽量小？如果高次项的系数 w 很大，模型曲线会变得过于曲折，紧密贴合训练数据点。较大的参数值在遇到训练数据的微小变化时，可能导致模型输出产生较大波动。会使部分参数 w 趋向于 0 ，意味着对应的特征在模型中不起作用，从而实现了特征选择。

L2 正则化（Ridge Regression）

Elastic Net

 

        ρ 是比例系数（0≤ρ≤1 ），用于调节 L1 和 L2 正则项的权重。

 L1 正则化和 L2 正则化的对比

特性	L1 正则化（Lasso）	L2 正则化（Ridge）
数学形式	绝对值和	平方和
稀疏性	✅ 产生稀疏解，部分权重=0	❌ 权重接近0但不等于0
特征选择	✅ 自动特征选择，剔除无关特征	❌ 保留所有特征，仅降低权重
参数平滑	❌ 部分参数归零，其余可能较大	✅ 参数平滑，权重均匀缩小
鲁棒性	❌ 对异常值敏感	✅ 对异常值更稳定
解的唯一性	❌ 可能多解（非唯一）	✅ 唯一解（严格凸优化）
适用场景	高维数据、特征选择	特征相关性强、需稳定解，避免极端参数值，提高泛化能力
几何约束	菱形（稀疏顶点解）	圆形（均匀收缩）

回归的评价指标

均方误差

均方根误差

平均绝对误差

 

逻辑回归（Logistic Regression）

        虽名称含 “回归” ，但主要用于分类问题，尤其是二分类，也可扩展到多分类。基于线性回归，通过 Sigmoid 函数σ(z)将线性组合结果z转化为概率值，预测样本属于某一类的概率。

广义线性模型（Generalized Linear Model, GLM）

        w 是权重向量，x 是输入特征向量 ，b 是偏置项，g是链接函数的逆函数，链接函数g 的作用是将线性组合的结果映射到合适的范围。

        比如逻辑回归是广义线性模型的一种，g 为 链接函数Sigmoid 函数的逆函数。