刚刚做到一道题，其中一个步骤让我深思了许久：
通过等价无穷小的公式 ~ x，可以将分母先变换成
。
但上面的为什么消失了？
它的等价无穷小等于1吗？似乎只有这种可能。
于是我开始验算：是不是当e的次数为负数时，这个指数函数的复合函数的等价无穷小都为1。
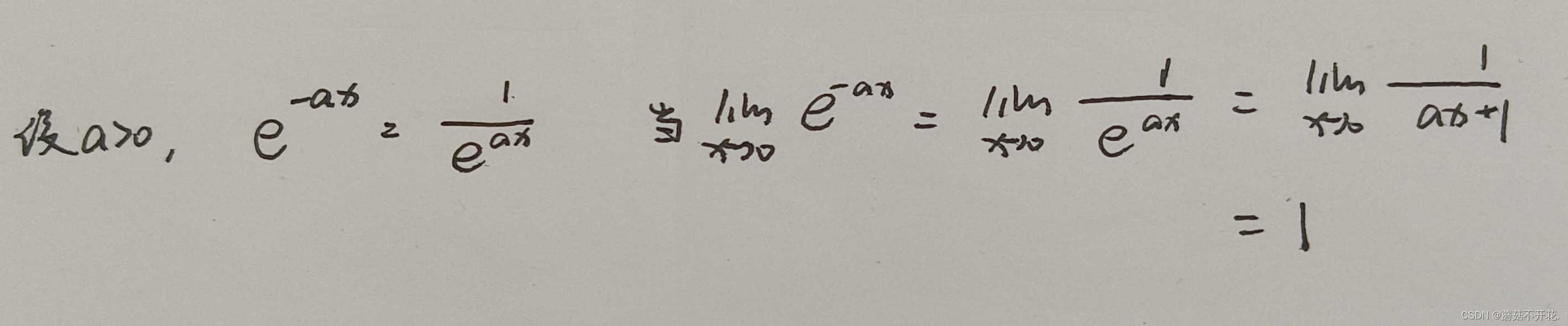
在这个验算过程中，我突然意识到，不需要e的次数为负数这个条件，因为我用到了~x+1这个等价无穷小公式，而当x→0时，若直接代入，就能得出
=1。
所以...想要让这个e的复合函数的等价无穷小为1，似乎只需要满足e的次数上的函数趋于0即可，而恰好，想用等价无穷小的前提也是e的次数上的函数趋于0~
哇！那如果这个公式可以这么用，我们做题再遇到e的几次方岂不是简单了很多！但还需要求证。而在今天做这道题之前，我从来都没有意识到这一点，于是蘑·虚心求教·菇同学立刻去询问了老师：
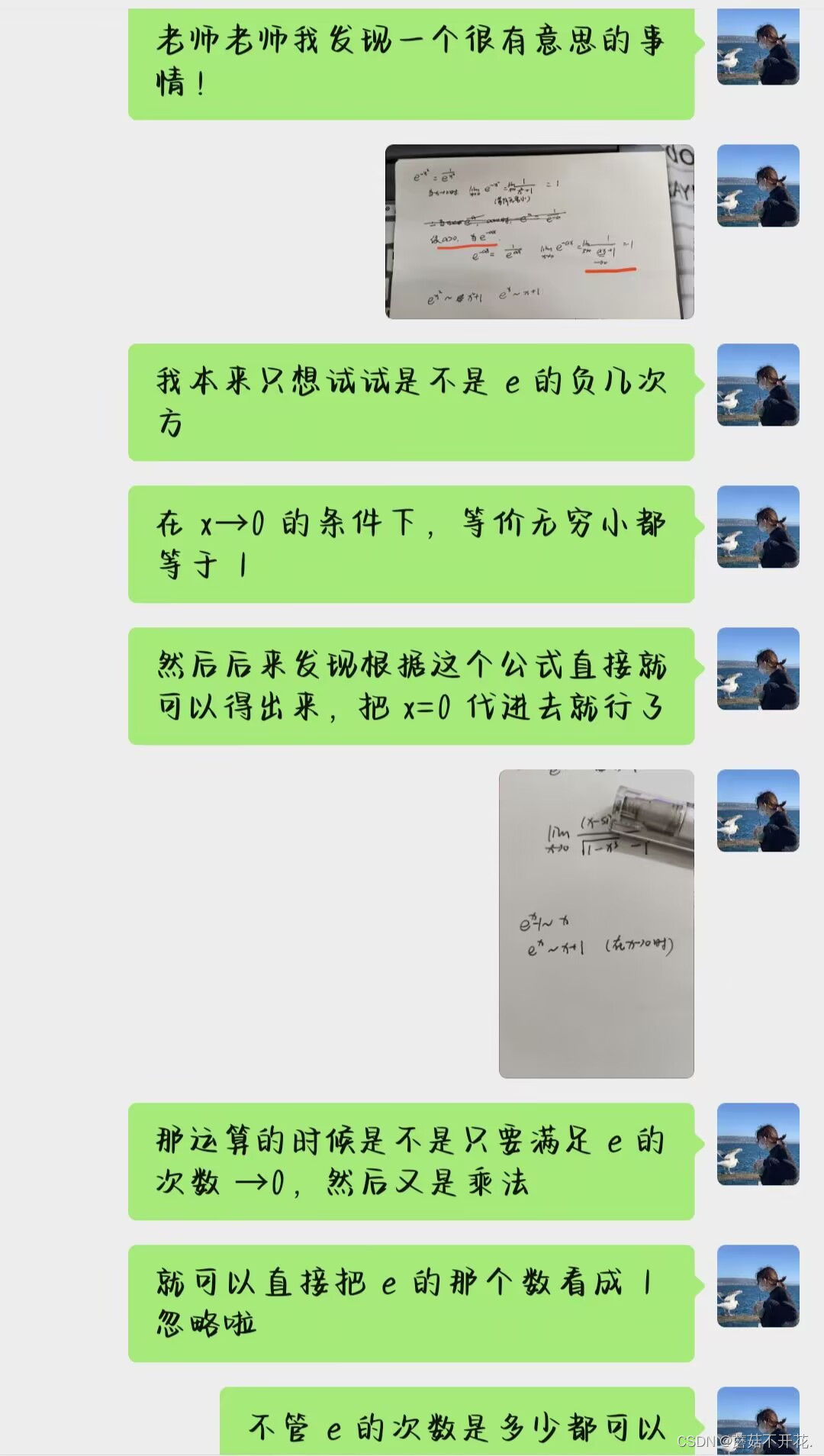
老师的回答是：
可以的！只要使用时注意等价无穷小的使用条件即可，运算时可以当成1来看，这样对我们的运算都可以简便许多了，否则还需要带着指数函数的复合函数进行洛必达求导等步骤。
这是今天的一个小发现（对于我来说），如果有错误的地方恳请指出~
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
