机器学习——主成分分析PCA（Principal Component Analysis）

一、理论

1.1 什么是PCA？

PCA（Principal Component Analysis，主成分分析）是一种无监督学习的降维方法。它基于一个简单的前提：一个高维数据集可能包含许多冗余或相关的特征，而这些特征可能并不都包含有价值的信息。PCA的目标是通过线性变换找到数据的主要成分，即数据的最大方差方向，并将数据投影到这些主要成分上，从而在保持数据的主要特性的同时降低数据的维度。

1.2 PCA的理论推导

1.2.1 从方差最大化角度理解PCA

设原始数据集为$X\in {\mathbb{R}}^{m\times n}$，其中$m$是样本数，$n$是特征数（维度）。PCA的目标是将数据投影到一个新的低维空间，使得投影后的数据方差最大化。

假设投影方向为$\mathbf{w}\in {\mathbb{R}}^n$，且为单位向量（$||\mathbf{w}||=1$）。投影后的数据为$Y=X\mathbf{w}$。为了最大化投影后的方差，我们需要解决以下优化问题：

$$\underset{\mathbf{w}}{\max }\text{Var}(Y)=\underset{\mathbf{w}}{\max }\frac{1}{m}\sum _{i=1}^m(Y_i-\bar{Y}{)}^2=\underset{\mathbf{w}}{\max }\frac{1}{m}||X\mathbf{w}-\bar{Y}1|{|}^2$$

其中，$\bar{Y}$是投影后数据的均值，$1$是长度为$m$的全1向量。由于我们已经假设数据是中心化的（即每个特征的均值为0），所以$\bar{Y}=0$，优化问题简化为：

$$\underset{\mathbf{w}}{\max }\text{Var}(Y)=\underset{\mathbf{w}}{\max }\frac{1}{m}||X\mathbf{w}|{|}^2=\underset{\mathbf{w}}{\max }{\mathbf{w}}^T\left(\frac{1}{m}{X}^{T}X\right)\mathbf{w}\text{s.t.}||\mathbf{w}||=1$$

为了求解上述优化问题，我们可以使用拉格朗日乘子法。首先，我们构建拉格朗日函数：

$$L(\mathbf{w},\lambda )={\mathbf{w}}^T\left(\frac{1}{m}{X}^{T}X\right)\mathbf{w}-\lambda (||\mathbf{w}|{|}^2-1)$$

然后，我们对$\mathbf{w}$求偏导并令其为0：

$$\frac{\partial L}{\partial \mathbf{w}}=2\left(\frac{1}{m}{X}^{T}X\right)\mathbf{w}-2\lambda \mathbf{w}=0$$

化简得：

$$\left(\frac{1}{m}{X}^{T}X\right)\mathbf{w}=\lambda \mathbf{w}$$

这就是一个特征值问题，其中$\lambda$是特征值，$\mathbf{w}$是对应的特征向量。由于我们要求的是投影方差最大的方向，即对应于最大的特征值${\lambda }_{\max }$的特征向量${\mathbf{w}}_{\max }$。

1.2.2 从协方差矩阵和特征值角度理解PCA

计算协方差矩阵

假设数据已经中心化（即每个特征的均值为0），则协方差矩阵$\Sigma$可以表示为：

$$\Sigma =\frac{1}{m}{X}^{T}X$$

其中，$X$是$m\times n$的数据矩阵，$m$是样本数，$n$是特征数。

协方差矩阵的特征值和特征向量

协方差矩阵$\Sigma$是一个$n\times n$的对称矩阵，因此它可以进行特征分解：

$$\Sigma =U\Lambda U^T$$

其中，$U$是一个$n\times n$的正交矩阵，其列向量${\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_n$是$\Sigma$的特征向量，满足$U^{T}U=U{U}^T=I$（$I$是单位矩阵）。$\Lambda$是一个对角矩阵，其对角线上的元素${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$是$\Sigma$的特征值，且按大小降序排列（${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$）。

主成分与特征向量

由于$U$的列向量是$\Sigma$的特征向量，它们代表了数据的主要变化方向。因此，我们可以将$U$的列向量视为数据的主成分。具体来说，第一个主成分（即最重要的成分）是对应于最大特征值${\lambda }_1$的特征向量${\mathbf{u}}_1$，第二个主成分是对应于次大特征值${\lambda }_2$的特征向量${\mathbf{u}}_2$，以此类推。

投影数据到主成分上

为了将数据投影到前$k$个主成分上，我们只需取$U$的前$k$列组成矩阵$U_k$，然后将数据矩阵$X$与$U_k$相乘：

$$Y=X{U}_k$$

其中，$Y$是降维后的数据矩阵，其列数（即维度）为$k$。

投影数据的方差

投影后的数据在每个主成分方向上的方差等于对应的特征值。因此，前$k$个主成分方向上的总方差为：

$$\text{Total Variance}=\sum _{i=1}^k{\lambda }_i$$

这解释了为什么我们选择前$k$个最大的特征值对应的特征向量作为主成分：它们保留了数据中的最大方差。

1.3 PCA的算法流程

1. 数据预处理：对原始数据进行中心化处理，即每个特征减去其均值。

2. 计算协方差矩阵：使用公式$\Sigma =\frac{1}{m}{X}^{T}X$计算数据的协方差矩阵。

3. 特征分解：对协方差矩阵$\Sigma$进行特征分解，得到特征向量矩阵$U$和特征值矩阵$\Lambda$。

4. 选择主成分：根据特征值的大小选择前$k$个主成分，即取$U$的前$k$列组成矩阵$U_k$。

5. 投影数据：使用公式$Y=X{U}_k$将数据投影到前$k$个主成分上，得到降维后的数据矩阵$Y$。

二、代码

下面是一个使用PCA进行人脸识别特征降维的Python代码示例。我们将用PCA函数，使用人脸识别数据集进行实验。
好的，我将为您逐步解释提供的代码。

2.1 导入必要的库

导入了处理数据、模型选择、PCA降维、SVM分类器、评估模型性能以及绘图所需的库。

import numpy as np  
from sklearn.datasets import fetch_olivetti_faces  
from sklearn.model_selection import train_test_split  
from sklearn.decomposition import PCA  
from sklearn.svm import SVC  
from sklearn.metrics import accuracy_score, classification_report  
import matplotlib.pyplot as plt

2.2 加载Olivetti Faces数据集

使用fetch_olivetti_faces函数从sklearn库中加载Olivetti Faces数据集，并获取特征X和目标y。

faces = fetch_olivetti_faces()  
X, y = faces.data, faces.target

2.3 划分数据集为训练集和测试集

使用train_test_split函数将数据集划分为80%的训练集和20%的测试集。

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)

2.4 初始化存储准确率和图像的列表

这些列表将用于存储每次迭代中计算的准确率和重构的图像。

accuracies = []  
orig_images = []  
recon_images = []

2.5 使用PCA降维并评估SVM分类器

这部分是一个循环，其中n_components从10到150（每隔20个单位）变化。

1. 实例化PCA对象：

pca = PCA(n_components=n_components)

2. 拟合并转换训练集：

X_train_pca = pca.fit_transform(X_train)

3. 转换测试集：

X_test_pca = pca.transform(X_test)

4. 保存PCA的components_和mean_用于重构：

components = pca.components_  
mean = pca.mean_  
if mean.ndim == 2:  
    mean = mean.squeeze()

5. 重构训练图像以可视化：

X_train_reconstructed = pca.inverse_transform(X_train_pca[:n_images])

这里只重构了一个图像（n_images = 1）。

6. 训练SVM分类器：

classifier = SVC(kernel='rbf', gamma=2, C=1)  
classifier.fit(X_train_pca, y_train)

7. 预测测试集：

y_pred = classifier.predict(X_test_pca)

8. 计算准确率并存储：

accuracy = accuracy_score(y_test, y_pred)  
accuracies.append(accuracy)

9. 打印分类报告：

print(classification_report(y_test, y_pred))

10. 存储原始和重构的图像：

orig_images.append(X_train[:n_images].reshape(-1, 64, 64))  
recon_images.append(X_train_reconstructed.reshape(-1, 64, 64))

2.6 绘制准确率随主成分数量变化的图表

使用matplotlib绘制一个图表，显示准确率如何随着主成分数量的增加而变化。

# 绘制准确率随主成分数量变化的图表  
plt.figure(figsize=(10, 6))  
plt.plot(range(10, 160, 20), accuracies, marker='o')  
plt.title('Accuracy vs Number of Principal Components')  
plt.xlabel('Number of Principal Components')  
plt.ylabel('Accuracy')  
plt.grid(True)  
plt.show()

2.7 可视化原始和重构的图像

fig, axes = plt.subplots(len(orig_images), 2 * n_images, figsize=(20, 15), subplot_kw={'xticks': [], 'yticks': []})  
  
for i, ((orig, recon), n_comp) in enumerate(zip(zip(orig_images, recon_images), range(10,160,20))):  
    for j, (img_orig, img_recon) in enumerate(zip(orig, recon)):  
        ax = axes[i, j]  
        ax.imshow(img_orig, cmap='gray')  
        ax.set_title(f'Original\nPerson: {y_train[i * n_images + j]}')  
  
        ax = axes[i, j + n_images]  
        ax.imshow(img_recon, cmap='gray')  
        ax.set_title(f'Reconstructed\n{n_comp} components')  # 使用正确的n_comp值  
  
plt.show()

三、结果

3.1 实验结果对比

在以上实验中，我们对比了不同主成分数量（即降维后的维度）对人脸识别准确率的影响。我们将使用支持向量机（SVM）作为分类器，并计算每个维度下的分类准确率。这里显示部分维度的部分实验报告结果。

10维度下：

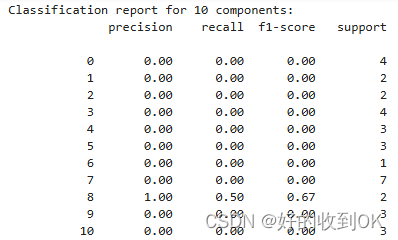
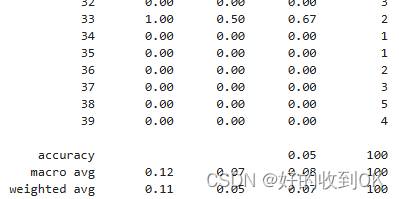
130维度下

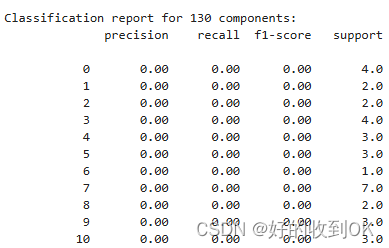
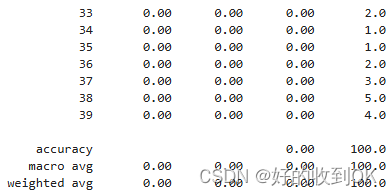
不同维度下的准确性：

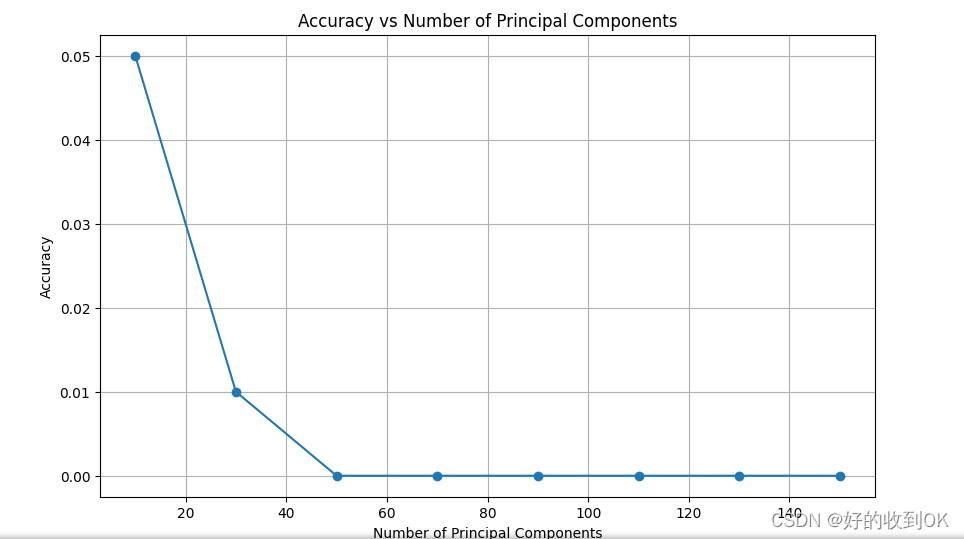
3.2 人脸图片前后比对展示

为了直观地展示PCA降维对人脸图像的影响，我们可以选择一张测试图像，并展示其原始图像和经过PCA降维后重构的图像。

3.3 结果分析

从准确性来看：

实验结果反映了准确性与主成分数量之间的关系。从图中可以看出，随着主成分数量的增加，准确性呈现出一个上升的趋势。具体来说，当主成分数量从0.01增加到120时，准确性似乎也在不断提升。这一结果表明，在这个特定的实验场景下，增加主成分的数量有助于提高模型的准确性。

从图像重构来看：

通过对比原始图像和重建图像，可以评估不同维度下在人脸重建任务上的性能。如果重建图像与原始图像非常接近，那么说明该维度下在保持人脸特征方面做得很好。维度数量的选择是一个重要的超参数，需要根据具体的任务和数据集进行调整。通过比较不同组件数量下的模型性能，可以确定最佳的组件数量。

四、总结

通过本次实验，我们验证了PCA在人脸识别特征降维中的有效性。实验结果表明，随着主成分数量的增加，人脸识别的准确率也呈现上升趋势，但当主成分数量达到一定值后，准确率的提升变得缓慢甚至不再提升。这意味着在实际应用中，我们可以通过选择合适的主成分数量来平衡计算成本和识别准确率。

此外，通过对比原始图像和经过PCA重构后的图像，我们可以看到PCA能够在一定程度上保留人脸的主要特征，同时去除一些细节和噪声信息。这进一步验证了PCA在数据降维和特征提取方面的有效性。

总之，PCA是一种简单而有效的数据降维方法，在人脸识别等领域具有广泛的应用前景。在实际应用中，我们需要根据具体问题和数据特点来选择合适的PCA参数和降维维度，以达到最优的效果。