一、机器学习和深度学习简介
深度学习的主题最近非常受欢迎，在这个过程中，出现了几个术语，使区分它们变得相当复杂。人们可能会发现，由于主题之间大量的重叠，将每个领域整齐地分开是一项艰巨的任务。
本章通过讨论深度学习的历史背景以及该领域如何演变成今天的形式来介绍深度学习的主题。稍后，我们将通过简要介绍基础主题来介绍机器学习。从深度学习开始，我们将利用使用基本 Python 从机器学习中获得的构造。第二章开始使用 PyTorch 进行实际实现。
定义深度学习
深度学习是机器学习的一个子领域，它处理的算法非常类似于人脑的过度简化版本，解决了现代机器智能的一个巨大类别。在智能手机的应用生态系统(iOS 和 Android)中可以找到许多常见的例子:相机上的人脸检测，键盘上的自动纠正和预测文本，人工智能增强的美化应用，智能助手，如 Siri/Alexa/Google Assistant，Face-ID(iphone 上的人脸解锁)，YouTube 上的视频建议，脸书上的朋友建议，Snapchat 上的 cat filters，都是只为深度学习而制造的最先进的产品。本质上，深度学习在当今的数字生活中无处不在。
说实话，如果没有一些历史背景，定义深度学习可能会很复杂。
简史
人工智能(AI)发展到今天的历程可以大致分为四个部分:即基于规则的系统、基于知识的系统、机器和深度学习。虽然旅程中的粒度转换可以映射为几个重要的里程碑，但我们将覆盖一个更简单的概述。整个进化包含在“人工智能”这个更大的概念中。让我们采取一步一步的方法来解决这个宽泛的术语。
图 1-1
人工智能的前景
深度学习的旅程始于人工智能领域，人工智能是该领域的合法父母，其历史可以追溯到 20 世纪 50 年代。人工智能领域可以简单定义为机器思考和学习的能力。用更通俗的话来说，我们可以把它定义为以某种形式用智能帮助机器的过程，这样它们可以比以前更好地执行任务。上图 1-1 展示了一个简化的人工智能场景，上面提到的各个领域展示了一个子集。我们将在下一节更详细地探讨这些子集。
基于规则的系统
我们诱导到机器中的智能不一定是复杂的过程或能力；像一套规则这样简单的东西可以被定义为智力。第一代人工智能产品只是基于规则的系统，其中一套全面的规则被引导到机器，以映射所有的可能性。一台根据既定规则执行任务的机器会比一台僵化的机器(没有智能的机器)产生更有吸引力的结果。
现代等价物的一个更外行的例子是提款机。一旦通过验证，用户输入他们想要的金额，机器就会根据店内现有的纸币组合，用最少的钞票分发正确的金额。机器解决问题的逻辑(智能)是显式编码(设计)的。机器的设计者仔细考虑了所有的可能性，设计了一个可以用有限的时间和资源有计划地解决任务的系统。
人工智能早期的大部分成功都相当简单。这样的任务可以很容易地形式化描述，就像跳棋或国际象棋。能够容易地正式描述任务的概念是计算机程序能够或不能够容易地完成什么的核心。例如，考虑国际象棋比赛。国际象棋游戏的正式描述将是棋盘的表示、每个棋子如何移动的描述、开始的配置以及游戏结束时的配置的描述。有了这些形式化的概念，将下棋的人工智能程序建模为搜索就相对容易了，而且，如果有足够的计算资源，就有可能产生相对较好的下棋人工智能。
人工智能的第一个时代专注于此类任务，并取得了相当大的成功。该方法的核心是领域的符号表示和基于给定规则的符号操作(使用越来越复杂的算法来搜索解决方案空间以获得解决方案)。
必须注意，这些规则的正式定义是手工完成的。然而，这种早期的人工智能系统是相当通用的任务/问题解决者，任何可以正式描述的问题都可以用通用的方法来解决。
这种系统的关键限制是，国际象棋比赛对人工智能来说是一个相对容易的问题，因为问题集相对简单，可以很容易地形式化。人类日常解决的许多问题却并非如此(自然智能)。例如，考虑诊断一种疾病或把人类的语言转录成文本。这些人类可以完成但很难正式描述的任务，在人工智能的早期是一个挑战。
基于知识的系统
利用自然智能解决日常问题的挑战将人工智能的前景演变成了一种类似于人类的方法——即通过利用大量关于任务/问题领域的知识。鉴于这种观察，随后的人工智能系统依赖于大型知识库来获取关于问题/任务领域的知识。注意，这里使用的术语是知识，而不是信息或数据。就知识而言，我们只是指程序/算法可以推理的数据/信息。一个例子可以是一个地图的图形表示，它的边标有距离和交通流量(它是不断更新的)，允许程序推理两点之间的最短路径。
这种基于知识的系统代表了第二代人工智能，其中知识由专家汇编，并以允许算法/程序推理的方式表示。这种方法的核心是越来越复杂的知识表示和推理方法，以解决需要这种知识的任务/问题。这种复杂性的例子包括使用一阶逻辑对知识和概率表示进行编码，以捕捉和推理领域固有的不确定性。
这类系统面临并在一定程度上得到解决的主要挑战之一是许多领域固有的不确定性。人类相对擅长在未知和不确定的环境中进行推理。这里的一个关键观察是，即使我们对一个领域的知识也不是黑或白的，而是灰色的。在这个时代，对未知和不确定性的描述和推理取得了很大进展。在一些任务中取得了有限的成功，如在未知和不确定的情况下，依靠利用知识库进行杠杆作用和推理来诊断疾病。
这种系统的关键限制是需要手工编译来自专家的领域知识。收集、编译和维护这样的知识库使得这样的系统不切实际。在某些领域，收集和编辑这样的知识是极其困难的——例如，将语音转录成文本或者将文档从一种语言翻译成另一种语言。虽然人类可以很容易地学会做这样的任务，但手工编译和编码与任务相关的知识却极具挑战性——例如，英语语言和语法、口音和主题的知识。为了应对这些挑战，机器学习是前进的方向。
机器学习
在正式术语中，我们将机器学习定义为人工智能中无需显式编程即可添加智能的领域。人类通过学习获得任何任务的知识。鉴于这一观察，人工智能后续工作的重点在 10 到 20 年间转移到了基于提供给它们的数据来提高它们性能的算法上。该子领域的焦点是开发算法，该算法获取给定数据的任务/问题领域的相关知识。值得注意的是，这种知识获取依赖于标记数据和人类定义的标记数据的适当表示。
例如，考虑诊断疾病的问题。对于这样一项任务，人类专家将收集大量患者患有和未患有相关疾病的病例。然后，人类专家将识别许多有助于做出预测的特征——例如，患者的年龄和性别，以及许多诊断测试的结果，如血压、血糖等。人类专家将汇编所有这些数据，并以适当的形式表示出来——例如，通过缩放/标准化数据等。一旦准备好这些数据，机器学习算法就可以学习如何通过从标记的数据中进行归纳来推断患者是否患有疾病。注意，标记的数据由患有和未患有该疾病的患者组成。因此，从本质上来说，底层机器语言算法本质上是在给定输入(年龄、性别、诊断测试数据等特征)的情况下，寻找能够产生正确结果(疾病或无疾病)的数学函数。寻找最简单的数学函数来预测具有所需精度水平的输出是机器学习领域的核心。例如，与学习一项任务所需的示例数量或算法的时间复杂度相关的问题是 ML 领域已经提供了理论证明的答案的特定领域。这个领域已经成熟到一定程度，给定足够的数据、计算资源和人力资源来设计特征，一大类问题是可以解决的。
主流机器语言算法的关键限制是，将它们应用到一个新的问题领域需要大量的特征工程。例如，考虑在图像中识别物体的问题。使用传统的机器语言技术，这样的问题将需要大量的特征工程工作，其中专家识别并生成将被机器语言算法使用的特征。从某种意义上说，真正的智慧在于对特征的识别；机器语言算法只是学习如何结合这些特征来得出正确的答案。在应用机器语言算法之前，领域专家进行的这种特征识别或数据表示是人工智能中概念和实践的瓶颈。
这是一个概念瓶颈，因为如果领域专家正在识别特征，而机器语言算法只是学习组合并从中得出结论，这真的是人工智能吗？这是一个实际的瓶颈，因为通过传统的机器语言建立模型的过程受到所需的大量特征工程的限制。解决这个问题的人力是有限的。
深度学习
深度学习解决了机器学习系统的主要瓶颈。在这里，我们基本上把智能向前推进了一步，机器以自动化的方式为任务开发相关功能，而不是手工制作。人类从原始数据开始学习概念。例如，一个孩子看到一些特定动物(比如说猫)的例子，他很快就会学会辨认这种动物。学习过程不包括父母识别猫的特征，如它的胡须、皮毛或尾巴。人类学习从原始数据到结论，而没有明确的步骤，即识别特征并提供给学习者。从某种意义上说，人类从数据本身学习数据的适当表示。此外，他们将概念组织成一个层次结构，其中复杂的概念用基本的概念来表达。
深度学习领域的主要重点是学习数据的适当表示，以便这些数据可以用于得出结论。“深度学习”中的“深”字是指直接从原始数据中学习概念的层次结构的思想。深度学习在技术上更合适的术语是表示学习，更实用的术语是自动化特征工程。
相关领域的进展
值得注意的是其他领域的进步，如计算能力、存储成本等。在深度学习最近的兴趣和成功中发挥了关键作用。例如，考虑以下情况:
-
在过去十年中，收集、存储和处理大量数据的能力有了很大提高(例如，Apache Hadoop 生态系统)。
-
随着众包服务(如 Amazon Mechanical Turk)的出现，生成受监督的训练数据(带标签的数据——例如，用图片中的对象进行注释的图片)的能力有了很大提高。
-
图形处理单元(GPU)带来的计算能力的巨大提高使并行计算达到了新的高度。
-
自动微分的理论和软件实现(如 PyTorch 或 Theano)的进步加快了深度学习的开发和研究速度。
虽然这些进步对于深度学习来说是外围的，但它们在实现深度学习的进步方面发挥了很大的作用。
先决条件
阅读这本书的关键先决条件包括 Python 的工作知识以及线性代数、微积分和概率方面的一些课程。如果读者需要了解这些先决条件，他们应该参考以下内容。
-
Mark Pilgrim-a press Publications(2004 年)著深入研究 Python
-
《线性代数导论》(第五版)，吉尔伯特·斯特朗-韦尔斯利-剑桥出版社
-
吉尔伯特·斯特朗-韦尔斯利-剑桥出版社出版的《微积分》
-
拉里·乏色曼-施普林格(2010)的所有统计数据(第一节，章节 1 - 5 )
前方的路
这本书关注深度学习的关键概念及其使用 PyTorch 的实际实现。为了使用 PyTorch，您应该对 Python 编程有一个基本的了解。第二章介绍 PyTorch，后续章节讨论 PyTorch 中的其他重要结构。
在深入研究深度学习之前，我们需要讨论机器学习的基本构造。在本章的剩余部分，我们将通过一个虚拟的例子来探索机器学习的初级步骤。为了实现这些构造，我们将使用 Python，并再次使用 PyTorch 来实现。
安装所需的库
为了运行本书中示例的源代码，您需要安装许多库。我们建议安装 Anaconda Python 发行版( https://www.anaconda.com/products/individual )，它简化了安装所需包的过程(使用 conda 或 pip)。您需要的包列表包括 NumPy、matplotlib、scikit-learn 和 PyTorch。
PyTorch 不是作为 Anaconda 发行版的一部分安装的。您应该安装 PyTorch、torchtext 和 torchvision，以及 Anaconda 环境。
请注意，本书中的练习推荐使用 Python 3.6(及更高版本)。我们强烈建议在安装 Anaconda 发行版之后创建一个新的 Python 环境。
使用 Python 3.6 创建一个新环境(在 Linux/Mac 中使用终端或在 Windows 中使用命令提示符)，然后安装其他必要的软件包，如下所示:
conda create -n testenvironment python=3.6
conda activate testenvironment
pip install pytorch torchvision torchtext
有关 PyTorch 的更多帮助，请参考 https://pytorch.org/get-started/locally/ 的入门指南。
机器学习的概念
作为人类，我们直观地意识到学习的概念。它只是意味着随着时间的推移，在一项任务上做得更好。这个任务可以是体力的，比如学习开车，也可以是智力的，比如学习一门新语言。机器学习的学科重点是开发能够像人类一样学习的算法；也就是说，随着时间的推移和经验的积累，他们在一项任务上变得更好——从而在没有显式编程的情况下诱导智力。
要问的第一个问题是，为什么我们会对随着时间的推移，随着经验的积累而提高性能的算法的开发感兴趣。毕竟，许多算法的开发和实现都是为了解决不随时间推移而改善的现实问题；它们只是由人类开发，用软件实现，并完成工作。从银行业到电子商务，从汽车导航系统到登月飞船，算法无处不在，而且大多数算法不会随着时间的推移而改进。这些算法只是执行它们想要执行的任务，并不时需要一些维护。我们为什么需要机器学习？
这个问题的答案是，对于某些任务，开发一个通过经验学习/提高其性能的算法比手动开发一个算法更容易。尽管在这一点上，这对于读者来说似乎是不直观的，但我们将在本章中对此建立直觉。
机器学习可以大致分为监督学习，为模型提供带标签的训练数据进行学习，以及非监督学习，训练数据缺少标签。我们也有半监督学习和强化学习，但是现在，我们将把范围限制在监督机器学习。监督学习又可以分为两个区域:分类，用于离散结果，以及回归，用于连续结果。
二元分类
为了进一步讨论手头的问题，我们需要精确地定义一些我们一直在直觉上使用的术语，比如任务、学习、经验和改进。我们将从二进制分类的任务开始。
考虑一个抽象的问题领域，其中我们有形式为
)
的数据
其中x∈ℝnt5y= 1。
我们无法访问所有这些数据，只能访问一个子集 S ∈ D 。使用 S ，我们的任务是生成一个实现函数 f : x → y 的计算过程，这样我们就可以使用 f 对未知数据进行预测( x i ，yI)∉s让我们把 U ∈ D 表示为一组看不见的数据——即( x i ，yI)∉s和( x i
*我们用未见过的数据
)
的误差来衡量这个任务的性能
我们现在对这个任务有了一个精确的定义，那就是通过生成 f ，基于一些看到的数据 S ，将数据归类到两个类别中的一个( y = 1)。我们使用未知数据 U 上的误差 E ( f ， D ， U )来衡量性能(以及性能的提高)。所见数据的大小| S |在概念上等同于经验。在这种背景下，我们想要开发生成这样的函数 f (通常称为模型)的算法。一般来说，机器学习领域研究这种算法的发展，这种算法产生对这种和其他正式任务的看不见的数据进行预测的模型。(我们将在本章后面介绍多个这样的任务。)注意， x 通常被称为输入/输入变量，而 y 被称为输出/输出变量。
如同计算机科学中的任何其他学科一样，这种算法的计算特性是一个重要的方面；然而，除此之外，我们还希望有一个模型 f ，它可以实现更低的误差 E ( f ， D ， U )，并且∣ S ∣尽可能小。
现在让我们将这个抽象但精确的定义与现实世界的问题联系起来，这样我们的抽象就有了基础。假设一个电子商务网站想要为注册用户定制其登录页面，以显示他们可能有兴趣购买的产品。该网站有用户的历史数据，并希望实现这一功能，以增加销售。现在让我们看看这个现实世界的问题是如何映射到我们前面描述的二进制分类的抽象问题上的。
人们可能注意到的第一件事是，给定一个特定的用户和特定的产品，人们会希望预测该用户是否会购买该产品。由于这是要预测的值，它映射到 y = 1，这里我们将让 y = + 1 的值表示用户将购买该产品的预测，而y= 1 的值表示用户将不会购买该产品的预测。请注意，选择这些值没有特别的原因；我们可以交换这一点(让 y = + 1 表示不买的情况，让y= 1 表示买的情况)，不会有任何不同。我们只是使用 y = 1 来表示对数据进行分类的两个感兴趣的类别。接下来，我们假设我们可以将产品的属性和用户的购买和浏览历史表示为x∈ℝn。这一步在机器学习中被称为特征工程，我们将在本章的后面介绍。现在，只要说我们能够生成这样的映射就足够了。这样，我们就有了用户浏览和购买了什么、产品的属性以及用户是否购买了该产品的历史数据映射到{( x 1 ， y 1 )，( x 2 ， y 2 )，…( x n 现在，基于这些数据，我们想要生成一个函数或模型f*:x→y，我们可以使用它来确定特定用户将购买哪些产品，并使用它来填充用户的登录页面。我们可以通过为用户填充登录页面，查看他们是否购买产品，并评估错误 E ( f ， D ， U )来衡量模型在看不见的数据上做得有多好。*
回归
本节介绍另一项任务:回归。这里，我们有格式为d= {(x1，y1)，(x2， y 2 )，…(xn，y的数据 我们的任务是生成一个计算程序，实现函数f:x→y。 注意，与二进制分类中的二进制分类标签 y = 1 不同，我们使用实值预测。我们用看不见的数据的均方根误差(RMSE)来衡量这个任务的性能
)
Note
RMSE 只是取预测值和实际值之间的差值，对其求平方以考虑正负差值，取平均值以聚合所有看不见的数据，最后，求平方根以平衡平方运算。
与回归的抽象任务相对应的一个现实世界的问题是基于个人的金融历史来预测他们的信用分数，信用卡公司可以使用该信用分数来扩展信用额度。
一般化
现在让我们来看看机器学习中最重要的直觉是什么，那就是我们想要开发/生成对看不见的数据具有良好性能的模型。为了做到这一点，首先我们将介绍一个玩具数据集的回归任务。稍后，我们将使用不同复杂程度的相同数据集开发三个不同的模型，并研究结果如何不同，以便直观地理解概化的概念。
在清单 1-1 中，我们通过生成 100 个在-1 和 1 之间等距的值作为输入变量( x )来生成玩具数据集。我们基于y= 2+x+2x2+ϵ生成输出变量( y ，其中
是正态分布的噪声(随机变化)，0 是平均值，0.1 是标准差。清单 1-1 给出了这方面的代码，数据绘制在图 1-2 中。为了模拟可见和不可见的数据，我们使用前 80 个数据点作为可见数据，其余的作为不可见数据。也就是说，我们仅使用前 80 个数据点来构建模型，并使用剩余的数据点来评估模型。
图 1-2
玩具数据集
#import packages
import matplotlib.pyplot as plt
import numpy as np
#Generate a toy dataset
x = np.linspace(-1,1,100)
signal = 2 + x + 2 * x * x
noise = numpy.random.normal(0, 0.1, 100)
y = signal + noise
plt.plot(signal,'b');
plt.plot(y,'g')
plt.plot(noise, 'r')
plt.xlabel("x")
plt.ylabel("y")
plt.legend(["Without Noise", "With Noise", "Noise"], loc = 2)
plt.show()
#Extract training from the toy dataset
x_train = x[0:80]
y_train = y[0:80]
print("Shape of x_train:",x_train.shape)
print("Shape of y_train:",y_train.shape)
Output[]
Shape of x_train: (80,)
Shape of y_train: (80,)
Listing 1-1Generalization vs. Rote Learning
接下来，我们用一个非常简单的算法来生成一个模型，通常称为最小二乘。给定一个格式为 D = {( x 1 ， y 1 )，( x 2 ， y 2 )，…(xn， y 的数据集 最小二乘模型采用的形式是 y = βx ，其中 β 是一个向量，使得
被最小化。 这里， X 是一个矩阵，其中每一行是一个 x (因此，x∈ℝ∈m×n，其中 m 是示例的数量，在我们的例子中是 80)。 β 的值可以用封闭形式β=(XTX)—1XTy导出。我们正在掩饰最小二乘法的许多重要细节，但这些都是当前讨论的次要问题。更相关的细节是我们如何将输入变量转换成合适的形式。在我们的第一个模型中，我们将把 x 转换成一个值的向量[ * x * 0 ， x 1 ， x 2 ]。也就是说，如果 x = 2，就转化为【1，2，4】。在此转换之后，我们可以使用之前描述的公式生成最小二乘模型 β 。实际情况是，我们用一个二阶多项式(次数= 2)方程来逼近给定的数据，最小二乘算法只是简单地曲线拟合或生成每个x0，x1，x2 的系数。
我们可以使用 RMSE 度量在看不见的数据上评估模型。我们还可以计算训练数据的 RMSE 度量。图 [1-3 绘制了实际值和预测值，清单 1-2 显示了生成模型的源代码。
图 1-3
阶数= 1 的模型的实际值和预测值
#Create a function to build a regression model with parameterized degree of independent coefficients
def create_model(x_train,degree):
degree+=1
X_train = np.column_stack([np.power(x_train,i) for i in range(0,degree)])
model = np.dot(np.dot(np.linalg.inv(np.dot(X_train.transpose(),X_train)),X_train.transpose()),y_train)
plt.plot(x,y,'g')
plt.xlabel("x")
plt.ylabel("y")
predicted = np.dot(model, [np.power(x,i) for i in range(0,degree)])
plt.plot(x, predicted,'r')
plt.legend(["Actual", "Predicted"], loc = 2)
plt.title("Model with degree =3")
train_rmse1 = np.sqrt(np.sum(np.dot(y[0:80] - predicted[0:80], y_train - predicted[0:80])))
test_rmse1 = np.sqrt(np.sum(np.dot(y[80:] - predicted[80:], y[80:] - predicted[80:])))
print("Train RMSE(Degree = "+str(degree)+"):", round(train_rmse1,2))
print("Test RMSE (Degree = "+str(degree)+"):", round(test_rmse1,2))
plt.show()
#Create a model with degree = 1 using the function
create_model(x_train,1)
Output[]
Train RMSE(Degree = 1): 3.55
Test RMSE (Degree = 1): 7.56
Listing 1-2.Function to build model with parameterized number of co-efficients
类似地，列表 1-3 和图 1-4 对度数=2 的模型重复该练习。
图 1-5
阶数= 8 的模型的实际值和预测值
图 1-4
阶数= 2 的模型的实际值和预测值
#Create a model with degree=2
create_model(x_train,2)
Output[]
Train RMSE (Degree = 3) 1.01
Test RMSE (Degree = 3) 0.43
Listing 1-3.Creating a model with degree=2
接下来，如清单 1-4 所示，我们用最小二乘算法生成另一个模型，但是我们将把 x 转换为x0， x 1 ， x 2 ， x 3 ， x 4 ，也就是说，我们用次数= 8 的多项式来逼近给定的数据。
#Create a model with degree=8
create_model(x_train,8)
Output[]
Train RMSE(Degree = 8): 0.84
Test RMSE (Degree = 8): 35.44
Listing 1-4Model with degree=8
实际值和预测值绘制在图 1-3 、图 1-4 和图 1-5 中。清单 1-2 中提供了创建模型的源代码(函数)。
我们现在已经有了讨论一般化核心概念的所有细节。要问的关键问题是哪个模型更好——度数= 2 的模型，度数= 8 的模型，还是度数= 1 的模型？让我们首先对这三个模型进行一些观察。与所有其他两个模型相比，度数= 1 的模型在可见和不可见数据上都表现不佳。与度数= 2 的模型相比，度数= 8 的模型在可见数据上表现得更好。对于看不见的数据，度数= 2 的模型比度数= 8 的模型执行得更好。表 1-1 应该有助于阐明模型的解释。
表 1-1
比较三种模型的性能
| -  |我们现在考虑模型容量的重要概念，它对应于本例中多项式的次数。我们生成的数据使用带有一些噪声的二阶多项式(次数= 2)。然后，我们尝试使用三个模型(分别为 1 度、2 度和 8 度)来逼近数据。度数越高，模型的表达能力越强，也就是说，它可以容纳更多的变化。这种适应变化的能力对应于模型容量的概念。也就是说，我们说度= 8 的模型比度= 2 的模型具有更高的容量，而度= 2 的模型又比度= 1 的模型具有更高的容量。拥有更高的容量不总是一件好事吗？当我们考虑到所有真实世界的数据集都包含一些噪声，并且更高容量的模型除了拟合数据中的信号之外，还会拟合噪声时，事实证明并非如此。这就是为什么我们观察到，与度数= 8 的模型相比，度数= 2 的模型在看不见的数据上做得更好。在这个例子中，我们知道数据是如何产生的(用一个二阶多项式(次数= 2)和一些噪声)；因此，这个观察是相当琐碎的。然而，在现实世界中，我们不知道数据生成的底层机制。这让我们想到了机器学习中的一个基本挑战:模型真的一般化了吗？唯一真正的测试是对看不见的数据的性能。
在某种意义上，容量的概念对应于模型的简单性或简约性。具有高容量的模型可以近似更复杂的数据。这是模型有多少自由变量/系数。在我们的示例中，度= 1 的模型没有足够的能力来逼近数据。这通常被称为欠拟合。相应地，度数= 8 的模型具有额外的容量，并且过拟合数据。
作为一个思想实验，考虑如果我们有一个度数= 80 的模型会发生什么。假设我们有 80 个数据点作为训练数据，我们将有一个 80 次多项式来完美地逼近数据。这是根本没有学习的终极病理案例。该模型有 80 个系数，可以简单地记忆数据。这被称为死记硬背，过度适应的逻辑极端。这就是为什么模型的容量需要根据我们拥有的训练数据量进行调整。如果数据集很小，我们最好训练容量较低的模型。
正规化
基于模型容量、泛化、过拟合和欠拟合的思想，本节讨论正则化。这里的关键思想是惩罚模型的复杂性。最小二乘法的正则化版本采取的形式是 y = βx ，其中 β 是一个向量，使得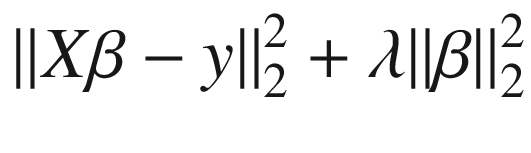
被最小化，而 λ 是控制复杂度的用户定义参数。在这里，通过引入术语
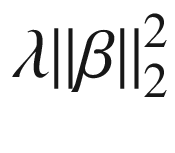，我们正在惩罚复杂的模型。要了解为什么会出现这种情况，请考虑使用 10 次多项式拟合最小二乘模型，但向量 β 中的值有八个零和两个非零。与此相反，考虑向量 β 中的所有值都不为零的情况。出于所有实际目的，前一个模型是度数= 2 的模型，并且具有更低的值
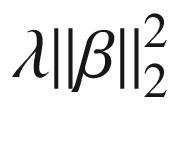。 λ 项使我们能够平衡训练数据的准确性和模型的复杂性。较低的 λ 值意味着更简单的模型。调整 λ 的值，我们可以通过平衡过拟合和欠拟合来提高模型在未知数据上的性能。
清单 1-5 展示了在保持模型系数不变但增加 λ 值的情况下，模型在不可见数据上的性能如何变化。
import matplotlib.pyplot as plt
import numpy as np
#Setting seed for reproducibility
np.random.seed(20)
#Create random data
x = np.linspace(-1,1,100)
signal = 2 + x + 2 * x * x
noise = np.random.normal(0, 0.1, 100)
y = signal + noise
x_train = x[0:80]
y_train = y[0:80]
train_rmse = []
test_rmse = []
degree = 80
#Define
a range of values for lambda
lambda_reg_values = np.linspace(0.01,0.99,100)
for lambda_reg in lambda_reg_values: #For each value of lambda, compute build model and compute performance for lambda_reg in lambda_reg_values:
X_train = np.column_stack([np.power(x_train,i) for i in range(0,degree)])
model = np.dot(np.dot(np.linalg.inv(np.dot(X_train.transpose(),X_train) + lambda_reg * np.identity(degree)),X_train.transpose()),y_train)
predicted = np.dot(model, [np.power(x,i) for i in range(0,degree)])
train_rmse.append(np.sqrt(np.sum(np.dot(y[0:80] - predicted[0:80], y_train - predicted[0:80]))))
test_rmse.append(np.sqrt(np.sum(np.dot(y[80:] - predicted[80:], y[80:] - predicted[80:]))))
#Plot the performance over train and test dataset.
plt.plot(lambda_reg_values, train_rmse)
plt.plot(lambda_reg_values, test_rmse)
plt.xlabel(r"$\lambda$")
plt.ylabel("RMSE")
plt.legend(["Train", "Test"], loc = 2)
plt.show()
Listing 1-5Regularization
我们可以利用封闭形式β=(XTX—λI)—1XTy来计算 β 的值。在清单 1-5 中，我们展示了将度数固定为值 80 并改变 λ 的值。训练 RMSE(已知数据)和测试 RMSE(未知数据)绘制在图 1-6 中。
图 1-6
正规化
我们看到，随着模型容量的增加，测试 RMSE 逐渐降低到最小值，然后逐渐增加，导致过度拟合。
摘要
本章涵盖了深度学习的简史，并介绍了机器学习的基础，包括监督学习的例子(分类和回归)。本章的重点是对看不见的示例进行概化的概念、训练数据的过拟合和欠拟合、模型的容量以及正则化的概念。鼓励读者尝试源代码清单中的示例。在下一章，我们将探索 PyTorch 作为开发深度学习模型的基础框架*
二、PyTorch 简介
最近几年见证了框架和工具的主要发布，以将深度学习大众化。今天，我们有太多的选择。本章旨在提供 PyTorch 的概述。我们将在整本书中广泛使用 PyTorch 来实现深度学习示例。注意，这一章不是 PyTorch 的全面指南，所以你应该参考这一章中建议的额外资料来更深入地理解这个框架。在本书后面的示例实现过程中，将提供一个基本概述和对该主题的必要补充。
事不宜迟，让我们先回顾一下您在考虑 PyTorch 时可能会遇到的一些更广泛的问题。
为什么我们需要深度学习框架？
开发一个深度神经网络并准备好它来解决今天的问题是一项非常艰巨的任务。在一个系统的流程中，有太多的部分需要连接和编排，以实现我们希望通过深度学习实现的目标。为了能够为研究和产品中的实验提供更简单、更快速、更高质量的解决方案，企业需要大量的抽象来完成繁重的基础任务。这将有助于研究人员和开发人员专注于重要的任务，而不是将大部分时间投入到基本操作上。深度学习框架和平台通过简单的功能提供了地面复杂任务的公平抽象，可以被研究人员和开发人员用作解决更大问题的工具。几个流行的选择是 Keras，PyTorch，TensorFlow，MXNet，Caffe，微软的 CNTK 等。
PyTorch 是什么？
PyTorch 是由脸书公司开发的开源机器学习和深度学习库。顾名思义，它是基于 Python 的，旨在通过提供 GPU 的无缝使用和提供最大灵活性和速度的深度学习平台，为 NumPy(在本章的示例中使用)提供更快的替代/替换。
为什么选择 PyTorch？
推荐 PyTorch 很简单。它提供了一个非常容易使用、扩展、开发和调试的框架。因为它是 Pythonic 化的，所以很容易被软件工程社区接受。对于研究人员和开发人员来说，完成任务同样容易。PyTorch 还使得深度学习模型易于生产化。它配备了高性能的 C++运行时，开发人员可以在生产环境中使用，同时避免通过 Python 进行推理。对于大多数熟悉 Python 的 NumPy 包的用户来说，PyTorch 将更容易过渡到。总的来说，PyTorch 为研究人员和开发人员提供了一个优秀的框架和平台，让他们在专注于重要任务的同时解决前沿的深度学习问题，并能够轻松地进行调试、实验和部署。
由于上述原因，PyTorch 在企业中被广泛采用。如果你关注深度学习的媒体，你可能会读到一些文章，提到一个新的大型组织采用 PyTorch。Yann Lecun 是深度学习领域的资深研究员，NYU 大学教授，脸书大学首席科学家(撰写本文时)在 2019 年 11 月发了以下推文:
“neur IPS 的 19 篇提到使用深度学习框架的论文中，超过 69%提到 PyTorch。PyTorch 在深度学习研究(ML/CV/NLP 会议)中遥遥领先。
有了足够的理由证明 PyTorch 是深度学习的一个值得选择，让我们开始吧。
这一切都始于张量
一般来说，深度学习中的任务将围绕处理图像、文本或表格数据(横截面以及时间序列)来生成结果，该结果是数字、标签、更多文本、另一个图像或这些的组合。简单的例子包括将图像分类为狗或猫，预测句子中的下一个单词，为图像生成标题，或者用新样式转换图像(比如 iOS/Android 上的 Prisma 应用程序)。这些任务中的每一项都需要将底层数据存储在特定的结构中。处理和开发这些解决方案将有几个中间阶段，这也需要特定的结构(例如，神经网络的权重)。一个通用于存储、表示和转换的结构是张量。
张量只不过是同一类型(通常是浮点数)对象的多维数组。虽然有点过于简化，但公平地说，在较低的抽象层次上，PyTorch 中的所有计算都是张量和张量上的运算。因此，为了让你能够流利地使用 PyTorch，你有必要对张量及其运算有一个直观的理解。还必须指出，这种对张量及其运算的介绍决不是完整的；您应该参考 PyTorch 文档来了解具体的用例。然而，指出这一章涵盖了张量及其运算的所有概念方面也是必要的。您应该在 Python 终端中尝试本节中的示例。(推荐 Jupyter 笔记本。)内化这种材料的最好方法是阅读概念，打出源代码，然后看着它执行。
张量是表示标量、矢量和矩阵的一种通用方式。张量可以定义为一个 n 维矩阵。一个 0 维张量(即单个数)叫做标量(图 2-1)；一维张量被称为矢量；二维张量被称为矩阵；三维张量也叫做立方体；等等。矩阵的维数也称为张量的秩。
图 2-1
0-n 维张量
PyTorch 是一个非常丰富的库，提供了许多功能，为深度学习提供了基础。本章简要介绍 PyTorch 为创建张量和执行数据管理操作、线性代数和数学运算提供的一些功能。
首先，让我们探索构造张量的多种方法。最基本的方法是使用 Python 中的列表来构造张量。下面的练习将演示一系列常用于构建深度学习应用程序的张量运算。为了帮助您更好地参与流程，代码和输出一直保持笔记本风格(交互流程:输入➤输出➤下一个输入➤下一个输出➤等等)。
创建张量
在清单 2-1 中，我们使用嵌套列表构建了一个二维张量。我们把这个张量存储为一个变量，然后看它的形状。
In [1]: import torch
torch.tensor([[0.1, 0.2],[0.3, 0.4]])
Out[1]:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000]])
Listing 2-1Creating a 2-Dimensional Tensor
形状表示张量的维数和用于推断张量秩的维数总数。在清单 2-2 中，dimension [2，2]将被推断为秩 2。
清单 2-2 探究了张量的形状。
In [1]: a = torch.tensor([[0.1, 0.2],[0.3, 0.4]])
In [2]: a.shape
Out[2]: torch.Size([2, 2])
In [3]: a
Out[3]:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000]])
Listing 2-2The Shape of a Tensor
我们可以尝试更多不同形状的例子。清单 2-3 探究不同形状的张量。
In [1]: b = torch.tensor([[0.1, 0.2],[0.3, 0.4],[0.5, 0.6]])
In [2]: b
Out[2]:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000],
[0.5000, 0.6000]])
In [3]: b.shape
Out[3]: torch.Size([3, 2])
Listing 2-3The shape of a tensor (continued)
还要注意，我们可以有任意维数的张量，而不仅仅是两个(如前面的例子)。清单 2-4 展示了三维张量的创建。
In [1]: c = torch.tensor([[[0.1],[0.2]],[[0.3],[0.4]]])
In [2]: c.shape
Out[2]: torch.Size([2, 2, 1])
In [3]: c
Out[3]:
tensor([[[0.1000],
[0.2000]],
[[0.3000],
[0.4000]]])
Listing 2-4Creating Tensors with Arbitrary Dimensions
正如我们可以用 Python 列表构建张量一样，我们也可以用 NumPy 数组构建张量。在将 NumPy 代码与 PyTorch 进行交互时，这一功能非常方便。清单 2-5 演示了使用 NumPy 创建张量。
In [1]: a = torch.tensor(numpy.array([[0.1, 0.2],[0.3, 0.4]]))
In [2]: a
Out[2]:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000]], dtype=torch.float64)
In [3]: a.shape
Out[3]: torch.Size([2, 2])
Listing 2-5Creating Tensors with NumPy
我们还可以使用from_numpy函数从现有的 NumPy n 维数组中创建一个张量。清单 2-6 演示了使用 PyTorch 的内置函数from_numpy从 NumPy 创建张量。
import numpy as np
a = np.array([1, 2, 3, 4, 5])
tensor_a = torch.from_numpy(a)
tensor_a
Output[]
tensor([1, 2, 3, 4, 5])
Listing 2-6Creating Tensors from NumPy
正如我们在引言中提到的，张量是同类型的多维数组。我们可以在构造张量时指定类型。在下面的例子中，我们用 32 位浮点数、64 位浮点数和 16 位浮点数初始化张量。PyTorch 总共定义了八种类型。(有关更多详细信息，请参考 PyTorch 文档。)清单 2-7 演示了用 PyTorch 中可用的几种流行数据类型来构造张量。
In [1]: a = torch.tensor([[0.1, 0.2],[0.3, 0.4]], dtype=torch.float32)
In [2]: a
Out[2]:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000]])
In [3]: a = torch.tensor([[0.1, 0.2],[0.3, 0.4]], dtype=torch.float64)
In [4]: a
Out[4]:
tensor([[0.1000, 0.2000],
[0.3000, 0.4000]], dtype=torch.float64)
In [5]: a = torch.tensor([[0.1, 0.2],[0.3, 0.4]], dtype=torch.float16)
In [6]: a
Out[6]:
tensor([[0.1000, 0.2000],
[0.3000, 0.3999]], dtype=torch.float16)
Listing 2-7Defining Tensor Datatypes
表 2-1 显示了不同的数据类型及其 PyTorch 等价物。
表 2-1
数据类型及其 PyTorch 等价物
|数据类型
|
PyTorch 当量
|
| — | — |
| 32 位浮点 | torch.float32 或 torch.float |
| 64 位浮点 | torch.float64 或 torch.double |
| 16 位浮点 | 火炬.浮动 16 或火炬.半 |
| 8 位整数(无符号) | torch.uint8 |
| 8 位整数(有符号) | torch.int8 |
| 16 位整数(有符号) | torch.int16 或 torch.short |
| 32 位整数(有符号) | torch.int32 或 torch.int |
| 64 位整数(有符号) | torch.int64 或 torch.long |
| 布尔代数学体系的 | 火炬.布尔 |
现在让我们看看构造张量的其他方法。一个常见的需求是构造一个用随机值填充的张量。清单 2-8 演示了创建一个具有随机值的定义形状的张量。
In [1]: r = torch.rand(2,2,2)
In [2]: r
Out[2]:
tensor([[[0.7993, 0.5940],
[0.3994, 0.7134]],
[[0.3102, 0.5175],
[0.6510, 0.7272]]])
In [3]: r.shape
Out[3]: torch.Size([2, 2, 2])
Listing 2-8Creating a Tensor with Random Values
另一个常见的要求是构造一个零张量。清单 2-9 展示了一个定义了全零形状的张量的创建。
In [1]: zeros = torch.zeros(2,2,3)
In [2]: zeros
Out[2]:
tensor([[[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.]]])
In [3]: zeros.shape
Out[3]: torch.Size([2, 2, 3])
Listing 2-9Creating
a Tensor Having All Zeros
同样，我们可以构造一个 1 的张量。清单 2-10 演示了创建一个定义了全 1 形状的张量。
In [1]: ones = torch.ones(2,2,3)
In [2]: ones
Out[2]:
tensor([[[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.]]])
In [3]: ones.shape
Out[3]: torch.Size([2, 2, 3])
Listing 2-10Creating a Tensor Having All Ones
另一个常见的需求是构造单位矩阵(张量)。清单 2-11 展示了一个单位矩阵张量的创建(即所有对角元素为 1)。
In [1] i = torch.eye(3)
In [2]: i
Out[2]:
tensor([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
In [3]: i.shape
Out[3]: torch.Size([3, 3])
Listing 2-11Creating an Identity Matix Tensor
我们也可以构造一个填充了任意值的任意形状的张量。清单 2-12 展示了一个任意值张量的创建。
In [1]: f = torch.full((3,3), 0.42)
In [2]: f
Out[2]:
tensor([[0.4200, 0.4200, 0.4200],
[0.4200, 0.4200, 0.4200],
[0.4200, 0.4200, 0.4200]])
In [3]: f.shape
Out[3]: torch.Size([3, 3])
Listing 2-12Creating a Tensor Filled with an Arbitrary Value
一个常见的用例也是用线性间隔的浮点数构建张量。清单 2-13 展示了使用线性间隔浮点数创建张量。
In [1]: lin = torch.linspace(0, 20, steps=5)
In [2]: lin
Out[2]: tensor([ 0., 5., 10., 15., 20.])
Listing 2-13Creating a Tensor with Linearly Spaced Floating-Point Numbers
类似地，清单 2-14 展示了用对数间隔浮点数构建张量。
In [1]: log = torch.logspace(-3, 3, steps=4)
In [2]: log
Out[2]: tensor([1.0000e-03, 1.0000e-01, 1.0000e+01, 1.0000e+03])
Listing 2-14Creating a Tensor with Logarithmically Spaced Floating-Point Numbers
有时我们需要创建维度与现有张量相似的张量。清单 2-15 中的例子说明了这一点。
In [1]: a = torch.tensor([[0.5, 0.5],[0.5, 0.5]])
In [2]: b = torch.zeros_like(a)
In [3]: b
Out[3]:
tensor([[0., 0.],
[0., 0.]])
In [4]: c = torch.ones_like(a)
In [5]: c
Out[5]:
tensor([[1., 1.],
[1., 1.]])
Listing 2-15Creating a Tensor with Dimensions Similar to Another Tensor
到目前为止，我们只考虑了浮点数。然而，PyTorch 张量并不局限于浮点数。下面是几个用整数和长整数构造张量的例子。顺便提一下，注意到dtype函数可以用来找到张量包含的对象的类型。清单 2-16 演示了创建一个整数数据类型的张量。
In [1]: i = torch.tensor([[1,2],[3,4]])
In [2]: i
Out[2]:
tensor([[1, 2],
[3, 4]])
In [3]: i.dtype
Out[3]: torch.int64
In [4]: i = torch.tensor([[1,2],[3,4]], dtype=torch.int)
In [5]: i
Out[5]:
tensor([[1, 2],
[3, 4]], dtype=torch.int32)
Listing 2-16Creating a Tensor with Integer Datatypes
类似地，清单 2-17 展示了具有整数范围的张量的构造。
In [1]: a = torch.arange(1,10, step=2)
In [2]: a
Out[2]: tensor([1, 3, 5, 7, 9])
Listing 2-17Creating a Tensor with a Range of Integers
同样，我们可以构造整数的随机排列。在清单 2-18 中，我们创建了一个整数随机排列的张量。
In [1]: r = torch.randperm(10)
In [2]: r
Out[2]: tensor([5, 3, 0, 2, 8, 1, 7, 4, 6, 9])
Listing 2-18Creating a Tensor with a Random Permutation of Integers
张量蒙格运算
看过张量和张量构造运算之后，现在让我们更深入地研究张量运算。我们将从访问张量的单个元素开始。下面的例子应该很熟悉，因为它与 Python 中的列表索引操作符相同。清单 2.19 演示了如何访问张量的单个成员。
In [1]: a = torch.tensor([[1,2],[3,4]])
In [2]: a
Out[2]:
tensor([[1, 2],
[3, 4]])
In [3]: a[0][0]
Out[3]: tensor(1)
In [4]: a[0][1]
Out[4]: tensor(2)
In [5]: a[1][0]
Out[5]: tensor(3)
In [6]: a[1][1]
Out[6]: tensor(4)
In [7]: a.shape
Out[7]: torch.Size([2, 2])
Listing 2-19Accessing Individual Members of a Tensor
要提取仅包含单个值的张量中的数据，应使用item方法。清单 2-20 演示了从张量中访问单个值。
In [1]: a = torch.tensor([[[0.42]]])
In [2]: a
Out[2]: tensor([[[0.4200]]])
In [3]: a.shape
Out[3]: torch.Size([1, 1, 1])
In [4]: a.item()
Out[4]: 0.41999998688697815
Listing 2-20Accessing a Single Value from a Tensor
view方法提供了一种重塑张量的简单方法。本质上，张量中的值被分配在连续的内存块中。PyTorch 张量本质上只是这个连续块上的一个视图。多个索引可以引用同一个存储，并以不同的形状表示张量。清单 2-21 展示了一个重塑张量的简单例子。
In [1]: a = torch.zeros(10)
In [2]: a
Out[2]: tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
In [3]: a.shape
Out[3]: torch.Size([10])
In [4]: b = a.view(2,5)
In [5]: b
Out[5]:
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
In [6]: b.shape
Out[6]: torch.Size([2, 5])
Listing 2-21Reshaping a Tensor
注意view方法如何重塑张量(元素放置的顺序)是很重要的。清单 2-22 演示了用“视图”方法重新整形后检验张量的大小。
In [1]: a = torch.arange(1,10)
In [2]: a
Out[2]: tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])
In [3]: a.shape
Out[3]: torch.Size([9])
In [4]: b = a.view(3,3)
In [5]: b
Out[5]:
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
In [6]: b.shape
Out[6]: torch.Size([3, 3])
Listing 2-22Verifying the Size of a Tensor After Reshaping with view
cat操作允许你沿着一个给定的维度连接一个张量列表。注意，cat操作有两个参数:要连接的张量列表和执行该操作的维度。清单 2-23 探究了两个张量的连接。
In [1]: a = torch.zeros(2,2)
In [2]: a
Out[2]:
tensor([[0., 0.],
[0., 0.]])
In [3]: a.shape
Out[3]: torch.Size([2, 2])
In [4]: b = torch.cat([a,a,a],0)
In [5]: b
Out[5]:
tensor([[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]])
In [6]: b.shape
Out[6]: torch.Size([6, 2])
In [7]: c = torch.cat([a,a,a],1)
In [8]: c
Out[8]:
tensor([[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.]])
In [9]: c.shape
Out[9]: torch.Size([2, 6])
Listing 2-23Concatenating Two Tensors
stack操作允许你通过沿着一个维度堆叠一系列张量来构造一个张量。合成张量的维数将增加一。清单 2-24 显示了堆叠操作如何沿着每个维度进行。注意，stack操作需要两个参数:张量列表和堆叠维度。维数的范围等于要叠加的张量的范围。
In [1]: a = torch.zeros(2,1)
In [2]: a
Out[2]:
tensor([[0.],
[0.]])
In [3]: a.shape
Out[3]: torch.Size([2, 1])
In [4]: b = torch.stack([a,a,a], 0)
In [5]: b
Out[5]:
tensor([[[0.],
[0.]],
[[0.],
[0.]],
[[0.],
[0.]]])
In [6]: b.shape
Out[6]: torch.Size([3, 2, 1])
In [7]: c = torch.stack([a,a,a], 1)
In [8]: c
Out[8]:
tensor([[[0.],
[0.],
[0.]],
[[0.],
[0.],
[0.]]])
In [9]: c.shape
Out[9]: torch.Size([2, 3, 1])
In [10]: d = torch.stack([a,a,a], 2)
In [11]: d
Out[11]:
tensor([[[0., 0., 0.]],
[[0., 0., 0.]]])
In [12]: d.shape
Out[12]: torch.Size([2, 1, 3])
Listing 2-24Stacking Tensors
chunk操作将张量沿给定方向分割成给定数量的部分。注意，第一个参数是张量；第二个参数是零件的数量；第三个参数是分区的方向。清单 2-25 演示了分块张量。
In [1]: a = torch.zeros(10, 1)
In [2]: a
Out[2]:
tensor([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.]])
In [3]: a.shape
Out[3]: torch.Size([10, 1])
In [4]: b = torch.chunk(a, 5, 0)
In [5]: b
Out[5]:
(tensor([[0.], [0.]]),
tensor([[0.], [0.]]),
tensor([[0.], [0.]]),
tensor([[0.], [0.]]),
tensor([[0.], [0.]]))
Listing 2-25Chunking Tensors
注意，当张量沿执行划分的维度的长度不是部分大小的倍数时，最后一个部分的元素比部分大小少。清单 2-26 展示了张量分块/截断的其他例子。
In [1]: d = torch.chunk(a, 3, 0)
In [2]: d
Out[2]:
(tensor([[0.],
[0.],
[0.],
[0.]]),
tensor([[0.],
[0.],
[0.],
[0.]]),
tensor([[0.],
[0.]]))
Listing 2-26Chunking Tensors (continued)
正如chunk方法使你能够将一个张量分割成给定数量的部分一样，split方法做同样的操作，但是给定部分的大小。请注意不同之处。基本上，chunk方法获取零件的数量，而split方法获取零件的尺寸。清单 2-27 展示了分裂张量。
In [1]: a = torch.zeros(10,1)
In [2]: a
Out[2]:
tensor([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.]])
In [3]: a.shape
Out[3]: torch.Size([10, 1])
In [4]: b = torch.split(a,2,0)
In [5]: b
Out[5]:
(tensor([[0.],[0.]]),
tensor([[0.],[0.]]),
tensor([[0.],[0.]]),
tensor([[0.],[0.]]),
tensor([[0.],[0.]]))
Listing 2-27Splitting Tensors
index_select方法允许你沿着给定的维度提取部分张量。注意，该方法有三个参数:要操作的张量、提取数据的维度和包含索引的张量。在清单 2-28 中，我们构建了一个 3x3 张量，然后沿着两个维度中的每一个提取数据。
In [1]: a = torch.FloatTensor([[1 ,2, 3],[4, 5, 6], [7, 8, 9]])
In [2]: a
Out[2]:
tensor([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: index = torch.LongTensor([0, 1])
In [5]: b = torch.index_select(a, 0, index)
In [6]: b
Out[6]:
tensor([[1., 2., 3.],
[4., 5., 6.]])
In [7]: b.shape
Out[7]: torch.Size([2, 3])
In [8]: c = torch.index_select(a, 1, index)
In [9]: c
Out[9]:
tensor([[1., 2.],
[4., 5.],
[7., 8.]])
In [10]: c.shape
Out[10]: torch.Size([3, 2])
Listing 2-28Extracting Parts of Tensors Using index_select
清单 2-29 中展示的masked_select方法允许你选择给定布尔掩码的元素。
In [1]: a = torch.FloatTensor([[1 ,2, 3],[4, 5, 6], [7, 8, 9]])
In [2]: a
Out[2]:
tensor([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: mask = torch.ByteTensor([[0, 1, 0],[1, 1, 1],[0, 1, 0]])
In [5]: mask
Out[5]:
tensor([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]], dtype=torch.uint8)
In [6]: mask.shape
Out[6]: torch.Size([3, 3])
In [7]: b = torch.masked_select(a, mask)
In [8]: b
Out[8]: tensor([2., 4., 5., 6., 8.])
In [9]: b.shape
Out[9]: torch.Size([5])
Listing 2-29Selecting Elements from a Tensor Using masked_select
squeeze方法删除所有值为 1 的维度，如清单 2-30 所示。
In [1]: a = torch.zeros(2,2,1)
In [2]: a
Out[2]:
tensor([[[0.],
[0.]],
[[0.],
[0.]]])
In [3]: a.shape
Out[3]: torch.Size([2, 2, 1])
In [4]: b = a.squeeze()
In [5]: b
Out[5]:
tensor([[0., 0.],
[0., 0.]])
In [6]: b.shape
Out[6]: torch.Size([2, 2])
Listing 2-30Reshaping a Tensor with the squeeze Method
类似地，unsqueeze方法添加一个值为 1 的新维度，如清单 2-31 所示。请注意如何在三个不同的位置添加额外的维度。
In [1]: a = torch.zeros(2,2)
In [2]: a
Out[2]:
tensor([[0., 0.],
[0., 0.]])
In [3]: a.shape
Out[3]: torch.Size([2, 2])
In [4]: b = torch.unsqueeze(a, 0)
In [5]: b
Out[5]:
tensor([[[0., 0.],
[0., 0.]]])
In [6]: b.shape
Out[6]: torch.Size([1, 2, 2])
In [7]: c = torch.unsqueeze(a, 1)
In [8]: c
Out[8]:
tensor([[[0., 0.]],
[[0., 0.]]])
In [9]: c.shape
Out[9]: torch.Size([2, 1, 2])
In [10]: d = torch.unsqueeze(a, 2)
In [11]: d
Out[11]:
tensor([[[0.],
[0.]],
[[0.],
[0.]]])
In [12]: d.shape
Out[12]: torch.Size([2, 2, 1])
Listing 2-31Reshaping a Tensor with the unsqueeze Method
unbind函数将给定的张量分解成沿给定维度的独立张量。清单 2-32 展示了使用unbind提取张量的各个部分。一个 3×3 张量沿着第一和第二维分解。注意，结果张量作为元组返回。
In [1]: a
Out[1]:
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
In [2]: a.shape
Out[2]: torch.Size([3, 3])
In [3]: torch.unbind(a, 0)
Out[3]: (tensor([1, 2, 3]), tensor([4, 5, 6]), tensor([7, 8, 9]))
In [4]: torch.unbind(a, 1)
Out[4]: (tensor([1, 4, 7]), tensor([2, 5, 8]), tensor([3, 6, 9]))
Listing 2-32Extracting Parts of a Tensor using unbind
清单 2-33 展示了使用where方法从现有张量创建一个张量。
In [1]: a = torch.zeros(3,3)
In [2]: a
Out[2]:
tensor([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: b = torch.ones(3,3)
In [5]: b
Out[5]:
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
In [6]: b.shape
Out[6]: torch.Size([3, 3])
In [7]: c = torch.rand(3,3)
In [8]: c
Out[8]:
tensor([[0.8452, 0.8095, 0.5903],
[0.7766, 0.6845, 0.4232],
[0.1080, 0.1946, 0.7541]])
In [9]: c.shape
Out[9]: torch.Size([3, 3])
In [10]: d = torch.where(c > 0.5, a, b)
In [11]: d
Out[11]:
tensor([[0., 0., 0.],
[0., 0., 1.],
[1., 1., 0.]])
In [12]: d.shape
Out[12]: torch.Size([3, 3])
Listing 2-33Constructing a Tensor from an Existing Tensor Using the where Method
清单 2-34 中所示的any和all方法分别使您能够检查给定条件在任何或所有情况下是否为真。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.3447, 0.4243, 0.6950],
[0.8801, 0.8502, 0.7759],
[0.6685, 0.9172, 0.4557]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: torch.any(a > 0)
Out[4]: tensor(1, dtype=torch.uint8)
In [5]: torch.any(a > 1.0)
Out[5]: tensor(0, dtype=torch.uint8)
In [6]: torch.all(a > 0)
Out[6]: tensor(1, dtype=torch.uint8)
In [7]: torch.all(a > 1.0)
Out[7]: tensor(0, dtype=torch.uint8)
Listing 2-34Conducting Logical Operations on Tensors Using the any and all Methods
view方法允许你重塑张量。清单 2-35 展示了重塑张量。请注意，使用-1 作为某个维度的大小意味着这是根据其他大小推断出来的。
In [1]: a = torch.arange(1,10)
In [2]: a
Out[2]: tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])
In [3]: b = a.view(3,3)
In [4]: b
Out[4]:
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
In [5]: b.shape
Out[5]: torch.Size([3, 3])
In [6]: c = a.view(3,-1)
In [7]: c
Out[7]:
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
In [8]: c.shape
Out[8]: torch.Size([3, 3])
Listing 2-35Reshaping tensors
flatten方法可用于从特定维度开始折叠给定张量的维度。清单 2-36 演示了使用flatten折叠张量的维度。
In [1]: a
Out[1]:
tensor([[[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]],
[[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]]])
In [2]: a.shape
Out[2]: torch.Size([2, 2, 2, 2])
In [3]: b = torch.flatten(a)
In [4]: b
Out[4]: tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
In [5]: b.shape
Out[5]: torch.Size([16])
In [6]: c = torch.flatten(a, start_dim=0)
In [7]: c
Out[7]: tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
In [8]: c.shape
Out[8]: torch.Size([16])
In [9]: d = torch.flatten(a, start_dim=1)
In [10]: d
Out[10]:
tensor([[1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1.]])
In [11]: d.shape
Out[11]: torch.Size([2, 8])
In [12]: e = torch.flatten(a, start_dim=2)
In [13]: e
Out[13]:
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
In [14]: e.shape
Out[14]: torch.Size([2, 2, 4])
In [15]: f = torch.flatten(a, start_dim=3)
In [16]: f
Out[16]:
tensor([[[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]],
[[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]]])
In [17]: f.shape
Out[17]: torch.Size([2, 2, 2, 2])
Listing 2-36Collapsing the Dimensions of a Tensor Using the flatten Method
gather方法允许我们在给定的位置沿着给定的维度从张量中提取值。清单 2-37 展示了使用gather从张量中提取值。
In [1]: a = torch.rand(4,4)
In [2]: a
Out[2]:
tensor([[0.6212, 0.7720, 0.8867, 0.4805],
[0.0323, 0.7763, 0.2295, 0.8778],
[0.5836, 0.3244, 0.3011, 0.5630],
[0.6748, 0.4487, 0.7052, 0.7185]])
In [3]: a.shape
Out[3]: torch.Size([4, 4])
In [4]: b = torch.LongTensor([[0,1,2,3]])
In [5]: b
Out[5]: tensor([[0, 1, 2, 3]])
In [6]: b.shape
Out[6]: torch.Size([1, 4])
In [7]: c = a.gather(0,b)
In [8]: c
Out[8]: tensor([[0.6212, 0.7763, 0.3011, 0.7185]])
In [9]: c.shape
Out[9]: torch.Size([1, 4])
In [10]: d = torch.LongTensor([[0],[1],[2],[3]])
In [11]: d
Out[11]:
tensor([[0],
[1],
[2],
[3]])
In [12]: d.shape
Out[12]: torch.Size([4, 1])
In [13]: e = a.gather(1,d)
In [14]: e
Out[14]:
tensor([[0.6212],
[0.7763],
[0.3011],
[0.7185]])
In [15]: e.shape
Out[15]: torch.Size([4, 1])
Listing 2-37Extracting Values from a Tensor Using the gather Method
类似地，scatter方法可用于将值放入给定位置的给定维度的张量中。清单 2-38 展示了用scatter增加张量的值。
In [1]: a = torch.rand(4,4)
In [2]: a
Out[2]:
tensor([[0.7159, 0.4922, 0.2732, 0.5839],
[0.0961, 0.9103, 0.9450, 0.6140],
[0.9439, 0.3156, 0.3493, 0.3125],
[0.1578, 0.1555, 0.6266, 0.4961]])
In [3]: a.shape
Out[3]: torch.Size([4, 4])
In [4]: index = torch.LongTensor([[0,1,2,3]])
In [5]: index
Out[5]: tensor([[0, 1, 2, 3]])
In [6]: index.shape
Out[6]: torch.Size([1, 4])
In [7]: values = torch.zeros(1,4)
In [8]: values
Out[8]: tensor([[0., 0., 0., 0.]])
In [9]: values.shape
Out[9]: torch.Size([1, 4])
In [10]: result = a.scatter(0, index, values)
In [11]: result
Out[11]:
tensor([[0.0000, 0.4922, 0.2732, 0.5839],
[0.0961, 0.0000, 0.9450, 0.6140],
[0.9439, 0.3156, 0.0000, 0.3125],
[0.1578, 0.1555, 0.6266, 0.0000]])
In [12]: result.shape
Out[12]: torch.Size([4, 4])
In [13]: a
Out[13]:
tensor([[0.7159, 0.4922, 0.2732, 0.5839],
[0.0961, 0.9103, 0.9450, 0.6140],
[0.9439, 0.3156, 0.3493, 0.3125],
[0.1578, 0.1555, 0.6266, 0.4961]])
Listing 2-38Augmenting a Tensor’s Values Using the scatter Method
数学运算
allclose方法允许我们在给定绝对或相对容差水平的情况下，检查两个张量中的值是否相同。这种方法帮助我们根据误差范围比较两个张量，在编写单元测试时非常方便。清单 2-39 说明了在公差水平内验证张量。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.9854, 0.2305, 0.1023],
[0.2054, 0.7064, 0.6115],
[0.6231, 0.0024, 0.8337]])
In [3]: b = a + a * 1e-3
In [4]: b
Out[4]:
tensor([[0.9864, 0.2307, 0.1024],
[0.2056, 0.7071, 0.6121],
[0.6237, 0.0024, 0.8345]])
In [5]: torch.allclose(a,b,rtol=1e-1)
Out[5]: True
In [6]: torch.allclose(a,b,rtol=1e-2)
Out[6]: True
In [7]: torch.allclose(a,b,rtol=1e-3)
Out[7]: True
In [8]: torch.allclose(a,b,rtol=1e-4)
Out[8]: False
In [9]: torch.allclose(a,b,atol=1e-1)
Out[9]: True
In [10]: torch.allclose(a,b,atol=1e-2)
Out[10]: True
In [11]: torch.allclose(a,b,atol=1e-3)
Out[11]: True
In [12]: torch.allclose(a,b,atol=1e-4)
Out[12]: False
Listing 2-39Validating Whether Given Tensors Are Within a Tolerance Level
argmax和argmin方法允许您获得给定维度上最大值和最小值的索引。清单 2-40 展示了提取张量中最小和最大值的维数。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.6295, 0.0995, 0.9350],
[0.7498, 0.7338, 0.2076],
[0.2302, 0.7524, 0.1993]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: torch.argmax(a, dim=0)
Out[4]: tensor([1, 2, 0])
In [5]: torch.argmax(a, dim=1)
Out[5]: tensor([2, 0, 1])
In [6]: torch.argmin(a, dim=0)
Out[6]: tensor([2, 0, 2])
In [7]: torch.argmin(a, dim=1)
Out[7]: tensor([1, 2, 2])
Listing 2-40Extracting Dimensions of Minimum and Maximum Values in a Given Tensor
类似地，清单 2-41 中所示的 argsort 函数给出了给定维度上排序值的索引。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.8380, 0.0738, 0.1025],
[0.7930, 0.5986, 0.9059],
[0.2777, 0.9390, 0.0700]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: torch.argsort(a, dim=0)
Out[4]:
tensor([[2, 0, 2],
[1, 1, 0],
[0, 2, 1]])
In [5]: torch.argsort(a, dim=1)
Out[5]:
tensor([[1, 2, 0],
[1, 0, 2],
[2, 0, 1]])
Listing 2-41Extracting the Indices of Sorted Values of a Tensor
清单 2-42 中展示的cumsum方法允许您计算给定维度上的累积和。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.2221, 0.7963, 0.5464],
[0.9116, 0.3773, 0.5860],
[0.5363, 0.7378, 0.3079]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: b = torch.cumsum(a, dim=0)
In [5]: b
Out[5]:
tensor([[0.2221, 0.7963, 0.5464],
[1.1337, 1.1736, 1.1324],
[1.6700, 1.9113, 1.4403]])
In [6]: b.shape
Out[6]: torch.Size([3, 3])
In [7]: c = torch.cumsum(a, dim=1)
In [8]: c
Out[8]:
tensor([[0.2221, 1.0183, 1.5647],
[0.9116, 1.2889, 1.8749],
[0.5363, 1.2741, 1.5820]])
In [9]: c.shape
Out[9]: torch.Size([3, 3])
Listing 2-42Computing the Cumulative Sum Along a Dimension of the Tensor
类似地，cumprod方法允许您计算给定维度上的累积积。清单 2-43 说明了累积积的计算。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.6971, 0.0358, 0.4075],
[0.2239, 0.2938, 0.3418],
[0.2482, 0.2108, 0.0709]])
In [3]: a.shape
Out[3]: torch.Size([3, 3])
In [4]: b = torch.cumprod(a, dim=0)
In [5]: b
Out[5]:
tensor([[0.6971, 0.0358, 0.4075],
[0.1561, 0.0105, 0.1393],
[0.0388, 0.0022, 0.0099]])
In [6]: b.shape
Out[6]: torch.Size([3, 3])
In [7]: c = torch.cumprod(a, dim=1)
In [8]: c
Out[8]:
tensor([[0.6971, 0.0250, 0.0102],
[0.2239, 0.0658, 0.0225],
[0.2482, 0.0523, 0.0037]])
In [9]: c.shape
Out[9]: torch.Size([3, 3])
Listing 2-43Computing the Cumulative Product Along a Dimension of the Tensor
abs方法允许你计算给定张量元素的绝对值。清单 2-44 展示了张量元素绝对值的计算。
In [1]: a = torch.tensor([[1,-1,1],[1,-1,1],[1,-1,1]])
In [2]: a
Out[2]:
tensor([[ 1, -1, 1],
[ 1, -1, 1],
[ 1, -1, 1]])
In [3]: b = torch.abs(a)
In [4]: b
Out[4]:
tensor([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]])
Listing 2-44Computing the Absolute Value of the elements of a Tensor
clamp功能允许您将元素限制在给定的最小值和最大值之间。清单 2-45 显示了张量内的箝位值。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.1181, 0.2922, 0.6639],
[0.9170, 0.1552, 0.3636],
[0.8511, 0.9194, 0.4650]])
In [3]: b = torch.clamp(a, min=0.25, max=0.50)
In [4]: b
Out[4]:
tensor([[0.2500, 0.2922, 0.5000],
[0.5000, 0.2500, 0.3636],
[0.5000, 0.5000, 0.4650]])
Listing 2-45Clamping Values Within a Tensor
ceil和floor函数允许你上舍入或下舍入给定张量的元素，如清单 2-46 所示。
In [1]: a = torch.rand(3,3) * 100
In [2]: a
Out[2]:
tensor([[18.6809, 56.6616, 10.2362],
[74.1378, 87.3797, 62.9137],
[42.4275, 82.0347, 96.2187]])
In [3]: b = torch.floor(a)
In [4]: b
Out[4]:
tensor([[18., 56., 10.],
[74., 87., 62.],
[42., 82., 96.]])
In [5]: c = torch.ceil(a)
In [6]: c
Out[6]:
tensor([[19., 57., 11.],
[75., 88., 63.],
[43., 83., 97.]])
Listing 2-46Ceil and floor operations within a tensor
元素式数学运算
现在让我们来看看一些基于元素的数学运算。这些运算被称为逐元素的数学运算，因为对张量的每个元素执行相同的运算。
mul函数允许你执行元素乘法，如清单 2-47 所示。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.6589, 0.9292, 0.0315],
[0.6033, 0.1030, 0.1090],
[0.4076, 0.7149, 0.8323]])
In [3]: b = torch.FloatTensor([[0, 1, 0],[1,1,1],[0,1,0]])
In [4]: b
Out[4]:
tensor([[0., 1., 0.],
[1., 1., 1.],
[0., 1., 0.]])
In [5]: c = torch.mul(a,b)
In [6]: c
Out[6]:
tensor([[0.0000, 0.9292, 0.0000],
[0.6033, 0.1030, 0.1090],
[0.0000, 0.7149, 0.0000]])
Listing 2-47Element-Wise Multiplication
类似地，我们有针对元素划分的div方法。清单 2-48 展示了张量的元素划分。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.9209, 0.8241, 0.6200],
[0.2758, 0.8846, 0.5146],
[0.1822, 0.2511, 0.3807]])
In [3]: b = torch.FloatTensor([[1, 2, 1],[2,2,2],[1,2,1]])
In [4]: b
Out[4]:
tensor([[1., 2., 1.],
[2., 2., 2.],
[1., 2., 1.]])
In [5]: c = torch.div(a,b)
In [6]: c
Out[6]:
tensor([[0.9209, 0.4121, 0.6200],
[0.1379, 0.4423, 0.2573],
[0.1822, 0.1256, 0.3807]])
Listing 2-48Element-Wise Division
张量中的三角运算
在深度学习中，我们还会在训练张量的过程中对它们进行一些三角运算。在本节中，我们将简要介绍 PyTorch 中常用的几个重要函数。清单 2-49 说明了基本的三角运算。
In [1]: a = torch.linspace(-1.0, 1.0, steps=10)
In [2]: a
Out[2]:
tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556, 0.7778, 1.0000])
In [3]: torch.sin(a)
Out[3]:
tensor([-0.8415, -0.7017, -0.5274, -0.3272, -0.1109, 0.1109, 0.3272, 0.5274, 0.7017, 0.8415])
In [4]: torch.cos(a)
Out[4]:
tensor([0.5403, 0.7125, 0.8496, 0.9450, 0.9938, 0.9938, 0.9450, 0.8496, 0.7125, 0.5403])
In [5]: torch.tan(a)
Out[5]:
tensor([-1.5574, -0.9849, -0.6208, -0.3463, -0.1116, 0.1116, 0.3463, 0.6208, 0.9849, 1.5574])
In [6]: torch.asin(a)
Out[6]:
tensor([-1.5708, -0.8911, -0.5890, -0.3398, -0.1113, 0.1113, 0.3398, 0.5890, 0.8911, 1.5708])
In [7]: torch.acos(a)
Out[7]:
tensor([3.1416, 2.4619, 2.1598, 1.9106, 1.6821, 1.4595, 1.2310, 0.9818, 0.6797, 0.0000])
In [8]: torch.atan(a)
Out[8]:
tensor([-0.7854, -0.6610, -0.5071, -0.3218, -0.1107, 0.1107, 0.3218, 0.5071, 0.6610, 0.7854])
Listing 2-49Basic Trigonometric Operations for Tensors
清单 2-50 举例说明了机器学习中经常使用的几个函数——即sigmoid、tanh、log1p(计算 y = log(1+x))、erf(高斯误差函数)和erfinv(逆高斯误差函数)。
In [1]: a = torch.linspace(-1.0, 1.0, steps=10)
In [2]: a
Out[2]:
tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556, 0.7778, 1.0000])
In [3]: torch.sigmoid(a)
Out[3]:
tensor([0.2689, 0.3148, 0.3646, 0.4174, 0.4723, 0.5277, 0.5826, 0.6354, 0.6852, 0.7311])
In [4]: torch.tanh(a)
Out[4]:
tensor([-0.7616, -0.6514, -0.5047, -0.3215, -0.1107, 0.1107, 0.3215, 0.5047, 0.6514, 0.7616])
In [5]: torch.log1p(a)
Out[5]:
tensor([ -inf, -1.5041, -0.8109, -0.4055, -0.1178, 0.1054, 0.2877, 0.4418, 0.5754, 0.6931])
In [6]: torch.erf(a)
Out[6]:
tensor([-0.8427, -0.7286, -0.5679, -0.3626, -0.1249, 0.1249, 0.3626, 0.5679, 0.7286, 0.8427])
In [7]: torch.erfinv(a)
Out[7]:
tensor([ -inf, -0.8631, -0.5407, -0.3046, -0.0988, 0.0988, 0.3046, 0.5407, 0.8631, inf])
Listing 2-50Additional Trigonometric Operations for Tensors
张量的比较运算
现在让我们考虑一些允许我们比较张量元素的运算——即，ge(大于或等于)、le(小于或等于)、eq(等于)和ne(不等于)。清单 2-51 说明了张量的比较运算。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.3340, 0.6635, 0.9417],
[0.2229, 0.6039, 0.9349],
[0.1783, 0.6485, 0.0172]])
In [3]: b = torch.rand(3,3)
In [4]: b
Out[4]:
tensor([[0.3854, 0.0581, 0.2514],
[0.0510, 0.8652, 0.0233],
[0.0191, 0.8724, 0.0364]])
In [5]: torch.ge(a,b)
Out[5]:
tensor([[0, 1, 1],
[1, 0, 1],
[1, 0, 0]], dtype=torch.uint8)
In [6]: torch.le(a,b)
Out[6]:
tensor([[1, 0, 0],
[0, 1, 0],
[0, 1, 1]], dtype=torch.uint8)
In [7]: torch.eq(a,b)
Out[7]:
tensor([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]], dtype=torch.uint8)
In [8]: torch.ne(a,b)
Out[8]:
tensor([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]], dtype=torch.uint8)
Listing 2-51Comparison Operations for Tensors
线性代数运算
我们现在将使用 PyTorch 张量深入研究一些线性代数运算。
matmul函数允许你将两个张量相乘。清单 2-52 演示了张量的矩阵乘法。
In [1]: a = torch.ones(2,3)
In [2]: a
Out[2]:
tensor([[1., 1., 1.],
[1., 1., 1.]])
In [3]: a.shape
Out[3]: torch.Size([2, 3])
In [4]: b = torch.ones(3,2)
In [5]: b
Out[5]:
tensor([[1., 1.],
[1., 1.],
[1., 1.]])
In [6]: b.shape
Out[6]: torch.Size([3, 2])
In [7]: torch.matmul(a,b)
Out[7]:
tensor([[3., 3.],
[3., 3.]])
In [8]: c.shape
Out[8]: torch.Size([3, 5])
Listing 2-52Matrix Multiplication Operations for Tensors
addbmm函数(其中bmm代表批量矩阵-矩阵乘积)允许您执行计算 p * m + q * [a1 * b1 + a2 * b2 +…]，其中 p 和 q 是标量，m、a1、b1、a2 和 b2 是张量。注意，addbmm函数采用默认值等于 1 的参数p和q，并且通过沿第一维堆叠张量来提供诸如a1和a2的张量。清单 2-53 展示了张量的批量矩阵-矩阵加法。
In [1]: a = torch.ones(2, 2, 3)
In [2]: a
Out[2]:
tensor([[[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.]]])
In [3]: a.shape
Out[3]: torch.Size([2, 2, 3])
In [4]: b = torch.ones(2, 3, 2)
In [5]: b
Out[5]:
tensor([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
In [6]: b.shape
Out[6]: torch.Size([2, 3, 2])
In [7]: m = torch.ones(2,2)
In [8]: m
Out[8]:
tensor([[1., 1.],
[1., 1.]])
In [9]: m.shape
Out[9]: torch.Size([2, 2])
In [10]: torch.addbmm(2, m, 3, a, b)
Out[10]:
tensor([[20., 20.],
[20., 20.]])
In [11]: torch.addbmm(1, m, 1, a, b)
Out[11]:
tensor([[7., 7.],
[7., 7.]])
In [12]: torch.addbmm(m, a, b)
Out[12]:
tensor([[7., 7.],
[7., 7.]])
Listing 2-53Batch Matrix-Matrix Addition of Tensors
addmm函数是addbmm的非批处理版本，它允许您执行计算 p * m + q * a * b，其中 p 和 q 是标量，m、a 和 b 是张量。注意，addmm函数将参数p和q的默认值设为 1。清单 2-54 展示了非批量矩阵——张量的矩阵加法。
In [1]: a = torch.ones(2, 3)
In [2]: a
Out[2]:
tensor([[1., 1., 1.],
[1., 1., 1.]])
In [3]: a.shape
Out[3]: torch.Size([2, 3])
In [4]: b = torch.ones(3, 2)
In [5]: b
Out[5]:
tensor([[1., 1.],
[1., 1.],
[1., 1.]])
In [6]: b.shape
Out[6]: torch.Size([3, 2])
In [7]: m = torch.ones(2,2)
In [8]: m
Out[8]:
tensor([[1., 1.],
[1., 1.]])
In [9]: m.shape
Out[9]: torch.Size([2, 2])
In [10]: torch.addmm(m, a, b)
Out[10]:
tensor([[4., 4.],
[4., 4.]])
In [11]: torch.addmm(2, m, 3, a, b)
Out[11]:
tensor([[11., 11.],
[11., 11.]])
In [12]: torch.addmm(1, m, 1, a, b)
Out[12]:
tensor([[4., 4.],
[4., 4.]])
Listing 2-54Non Batch Matrix-Matrix Addition of Tensors
addmv函数(matrix-vector)允许你执行计算 p * m + q * a * b，其中 p 和 q 是标量，m 和 a 是矩阵，b 是向量。请注意，addmv采用默认值等于 1 的参数p和q。清单 2-55 展示了张量的矩阵向量加法。
In [1]: a = torch.ones(2, 3)
In [2]: a
Out[2]:
tensor([[1., 1., 1.],
[1., 1., 1.]])
In [3]: a.shape
Out[3]: torch.Size([2, 3])
In [4]: b = torch.ones(3)
In [5]: b
Out[5]: tensor([1., 1., 1.])
In [6]: b.shape
Out[6]: torch.Size([3])
In [7]: m = torch.ones(2)
In [8]: m
Out[8]: tensor([1., 1.])
In [9]: m.shape
Out[9]: torch.Size([2])
In [10]: torch.addmv(2,m,3,a,b)
Out[10]: tensor([11., 11.])
In [11]: torch.addmv(1,m,1,a,b)
Out[11]: tensor([4., 4.])
In [12]: torch.addmv(m,a,b)
Out[12]: tensor([4., 4.])
Listing 2-55Matrix Vector Addition of Tensors
addr函数允许您执行两个向量的外积，并将其添加到给定的矩阵中。线性代数中两个向量的外积是一个矩阵。比如你有一个 m 元素(1 维)的向量 V，另一个 n 元素(1 维)的向量 U，那么 V 和 U 的外积就是一个 m × n 形状的矩阵。
V= [v1, v2, v3..., vm]
U = [u1, u2, ......un]
V ⊕ U = A
A = [ v1u1, v1u2, .... , v1um,
v2u1, v2,u2,.......v2um,
.....
vnu1, vnu2, .......vnum]
在 PyTorch 中，函数期望第一个参数作为我们需要添加结果外积的矩阵，后面是需要计算外积的向量。在清单 2-56 中，我们创建了两个向量(a 和 b)，每个向量有三个元素，并执行外积来创建一个 3 × 3 的矩阵，然后将其添加到另一个矩阵(m)中。
In [1]: a = torch.tensor([1.0, 2.0, 3.0])
In [2]: a
Out[2]: tensor([1., 2., 3.])
In [3]: a.shape
Out[3]: torch.Size([3])
In [4]: b = a
In [5]: m = torch.ones(3,3)
In [6]: m
Out[6]:
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
In [7]: m.shape
Out[7]: torch.Size([3, 3])
In [8]: torch.addr(m,a,b)
Out[8]:
tensor([[ 2., 3., 4.],
[ 3., 5., 7.],
[ 4., 7., 10.]])
In [9]: m = torch.zeros(3,3)
In [10]: m
Out[10]:
tensor([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
In [11]: torch.addr(m,a,b)
Out[11]:
tensor([[1., 2., 3.],
[2., 4., 6.],
[3., 6., 9.]])
Listing 2-56Outer Product of Vectors
baddbmm函数允许您执行计算 p1 * m + q * [a1 * b1]，p2 * m + q * [a2 * b2]，…，其中 p 和 q 是标量，m、p1、a1、b1、p2、a2 和 b2 是张量。注意baddbmm取默认值等于 1 的参数p和q，p1、a1、a2 等张量通过沿第一维叠加提供。清单 2-27 说明了baddbmm功能的使用。
In [1]: a = torch.ones(2,2,3)
In [2]: a
Out[2]:
tensor([[[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.]]])
In [3]: a.shape
Out[3]: torch.Size([2, 2, 3])
In [4]: b = torch.ones(2,3,2)
In [5]: b
Out[5]:
tensor([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
In [6]: b.shape
Out[6]: torch.Size([2, 3, 2])
In [7]: m = torch.ones(2, 2, 2)
In [8]: m
Out[8]:
tensor([[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]])
In [9]: m.shape
Out[9]: torch.Size([2, 2, 2])
In [10]: torch.baddbmm(1,m,1,a,b)
Out[10]:
tensor([[[4., 4.],
[4., 4.]],
[[4., 4.],
[4., 4.]]])
In [11]: torch.baddbmm(2,m,1,a,b)
Out[11]:
tensor([[[5., 5.],
[5., 5.]],
[[5., 5.],
[5., 5.]]])
In [12]: torch.baddbmm(1,m,2,a,b)
Out[12]:
tensor([[[7., 7.],
[7., 7.]],
[[7., 7.],
[7., 7.]]])
Listing 2-57The baddbmm Function
bmm函数允许你对张量执行批量矩阵乘法，如清单 2-58 所示。
In [1]: a = torch.ones(2,2,3)
In [2]: a
Out[2]:
tensor([[[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.]]])
In [3]: a.shape
Out[3]: torch.Size([2, 2, 3])
In [4]: b = torch.ones(2,3,2)
In [5]: b
Out[5]:
tensor([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
In [6]: b.shape
Out[6]: torch.Size([2, 3, 2])
In [7]: torch.bmm(a,b)
Out[7]:
tensor([[[3., 3.],
[3., 3.]],
[[3., 3.],
[3., 3.]]])
Listing 2-58Batch-Wise Matrix Multiplication
dot函数允许你计算张量的点积，如清单 2-59 所示。
In [1]: a = torch.rand(3)
In [2]: a
Out[2]: tensor([0.3998, 0.6383, 0.1169])
In [3]: b = torch.rand(3)
In [4]: b
Out[4]: tensor([0.9743, 0.2473, 0.7826])
In [5]: torch.dot(a,b)
Out[5]: tensor(0.6389)
Listing 2-59Computing the Dot Product of Tensors
eig函数允许你计算给定矩阵的特征值和特征向量。清单 2-60 演示了计算张量的特征值。我们首先计算特征值，然后确认结果匹配。请注意mm函数的使用，它允许您将两个矩阵相乘。
In [1]: a = torch.rand(3,3)
In [2]: a
Out[2]:
tensor([[0.1090, 0.2947, 0.5896],
[0.6438, 0.2429, 0.7332],
[0.5636, 0.9291, 0.3909]])
In [3]: values, vectors = torch.eig(a, eigenvectors=True)
In [4]: values
Out[4]:
tensor([[ 1.5308, 0.0000],
[-0.3940, 0.1086],
[-0.3940, -0.1086]])
In [5]: vectors
Out[5]:
tensor([[-0.4097, -0.6717, 0.0000],
[-0.5973, -0.0767, 0.3048],
[-0.6894, 0.6114, -0.2761]])
In [6]: values[0,0] * vectors[:,0].reshape(3,1)
Out[6]:
tensor([[-0.6272],
[-0.9144],
[-1.0554]])
In [7]: torch.mm(a, vectors[:,0].reshape(3,1))
Out[7]:
tensor([[-0.6272],
[-0.9144],
[-1.0554]])
Listing 2-60Computing Eigenvalues for a Tensor
清单 2-61 中展示的cross函数允许你计算两个张量的叉积。
In [1]: a = torch.rand(3)
In [2]: b = torch.rand(3)
In [3]: a
Out[3]: tensor([0.3308, 0.2168, 0.0932])
In [4]: b
Out[4]: tensor([0.3471, 0.2871, 0.6141])
In [5]: torch.cross(a,b)
Out[5]: tensor([ 0.1064, -0.1708, 0.0197])
Listing 2-61Computing the Cross Product of Two Tensors
如清单 2-62 所示，norm函数允许你计算给定张量的范数。
In [1]: a = torch.ones(4)
In [2]: a
Out[2]: tensor([1., 1., 1., 1.])
In [3]: torch.norm(a,1)
Out[3]: tensor(4.)
In [4]: torch.norm(a,2)
Out[4]: tensor(2.)
In [5]: torch.norm(a,3)
Out[5]: tensor(1.5874)
In [6]: torch.norm(a,4)
Out[6]: tensor(1.4142)
In [7]: torch.norm(a,5)
Out[7]: tensor(1.3195)
In [8]: torch.norm(a,float('inf'))
Out[8]: tensor(1.)
Listing 2-62Computing the Norm of a Tensor
renorm函数允许你通过除以范数来归一化一个向量。清单 2-63 演示了张量的规范化操作。
In [1]: a = torch.FloatTensor([[1,2,3,4]])
In [2]: a
Out[2]: tensor([[1., 2., 3., 4.]])
In [3]: torch.renorm(a, dim=0, p=2, maxnorm=1)
Out[3]: tensor([[0.1826, 0.3651, 0.5477, 0.7303]])
Listing 2-63Normalizing a Tensor
摘要
本章简要介绍 PyTorch，重点介绍张量和张量运算。本章讨论的几个张量运算将在接下来的几章中派上用场。你应该花时间和张量一起提高你的 PyTorch 技能。这对于定制深度学习网络和在出现不明错误时容易地调试流程将是非常有价值的。
常见的张量操作有view(重塑张量)size(打印张量的形状/大小)item(从单值张量中提取数据)squeeze(重塑张量)cat(连接张量)。此外，PyTorch 有两个独立的包(torchvision 和 torchtext ),它们提供了一套全面的处理图像(计算机视觉)和文本(自然语言处理)数据集的功能。我们将在第六章“卷积神经网络”和第七章“循环神经网络”中探索这些包的基本实用程序
作为一个库，PyTorch 为研究人员和实践者提供了一种出色的方法来大规模开发和训练深度学习实验，同时为几个构建块提供了简洁的抽象，同时还可以灵活地进行深度定制。在接下来的几章中，在实际实现深度学习模型时，您将看到 PyTorch 如何在后台处理如此多的事情，从而为用户提供大规模加速实验所需的速度和敏捷性。
下一章将关注基本前馈网络的基础——走向深度学习的第一步。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
