Scikit-Learn 1.4使用指南：无监督学习 密度估计 Density Estimation.

scikit-learn 1.6 官网中文文档翻译已经上线了，欢迎使用：http://www.aidoczh.com/scikit-learn/

密度估计涉及无监督学习、特征工程和数据建模。一些最受欢迎和有用的密度估计技术是混合模型，如高斯混合模型（ ~sklearn.mixture.GaussianMixture），以及基于邻居的方法，如核密度估计（ ~sklearn.neighbors.KernelDensity）。高斯混合模型在 聚类 <clustering>的背景下更详细地讨论，因为该技术也可用作无监督聚类方案。

密度估计是一个非常简单的概念，大多数人已经熟悉其中一种常见的密度估计技术：直方图。

密度估计：直方图

直方图是一种简单的数据可视化方法，其中定义了若干个区间（bin），并计算每个区间内的数据点数量。下图左上方的面板显示了一个直方图的示例：

然而，直方图的一个主要问题是，选择区间的方式可能对结果可视化产生不成比例的影响。考虑上图右上方的面板，它显示了相同数据的直方图，但区间向右移动了。两种可视化结果看起来完全不同，可能导致对数据的不同解释。

直观地说，我们也可以将直方图看作是一堆块，每个点对应一个块。通过将块堆叠在适当的网格空间中，我们可以恢复直方图。但是，如果我们不是在规则网格上堆叠块，而是将每个块居中在其表示的点上，并在每个位置上求和总高度会怎样呢？这个想法导致了下图左下方的可视化效果。它可能不像直方图那样干净，但是数据驱动块的位置意味着它更好地表示了底层数据。

这个可视化效果是核密度估计的一个例子，这里使用的是一个顶帽核（即每个点处的方形块）。通过使用更平滑的核，我们可以得到一个更平滑的分布。下图右下方的图表显示了一个高斯核密度估计，其中每个点对总体贡献了一个高斯曲线。结果是一个平滑的密度估计，它是从数据中推导出来的，并且作为点的分布的一个强大的非参数模型。

核密度估计

scikit-learn中的核密度估计实现在~sklearn.neighbors.KernelDensity估计器中，它使用Ball Tree或KD Tree进行高效查询（有关这些的讨论，请参见neighbors）。尽管上面的示例使用了一个一维数据集来简化，但核密度估计可以在任意维度上执行，尽管在实践中，维度的诅咒会导致其在高维中的性能下降。

在下图中，从双峰分布中抽取了100个点，并显示了三种内核选择的核密度估计结果：

很明显，核形状如何影响结果分布的平滑程度。scikit-learn的核密度估计器可以按以下方式使用：

>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.

这里我们使用了kernel='gaussian'，如上所示。从数学上讲，核是一个正函数$K(x;h)$，由带宽参数$h$控制。给定这个核形式，在一组点$x_i;i=1\cdots N$中的点$y$处的密度估计由以下公式给出：

$${\rho }_K(y)=\sum _{i=1}^{N}K(y-x_i;h)$$

这里的带宽充当平滑参数，控制结果中偏差和方差之间的权衡。较大的带宽会导致非常平滑（即高偏差）的密度分布。较小的带宽会导致非平滑（即高方差）的密度分布。

参数带宽控制着这种平滑。可以手动设置此参数，也可以使用Scott和Silvermann的估计方法。

~sklearn.neighbors.KernelDensity实现了几种常见的核形式，如下图所示：

核函数的数学表达式

这些核的形式如下：

• 高斯核（kernel = 'gaussian'）

  $K(x;h)\propto \exp (-\frac{x^2}{2h^2})$

• 顶帽核（kernel = 'tophat'）

  $K(x;h)\propto 1$ if $x<h$

• Epanechnikov核（kernel = 'epanechnikov'）

  $K(x;h)\propto 1-\frac{x^2}{h^2}$

• 指数核（kernel = 'exponential'）

  $K(x;h)\propto \exp (-x/h)$

• 线性核（kernel = 'linear'）

  $K(x;h)\propto 1-x/h$ if $x<h$

• 余弦核（kernel = 'cosine'）

  $K(x;h)\propto \cos (\frac{\pi x}{2h})$ if $x<h$

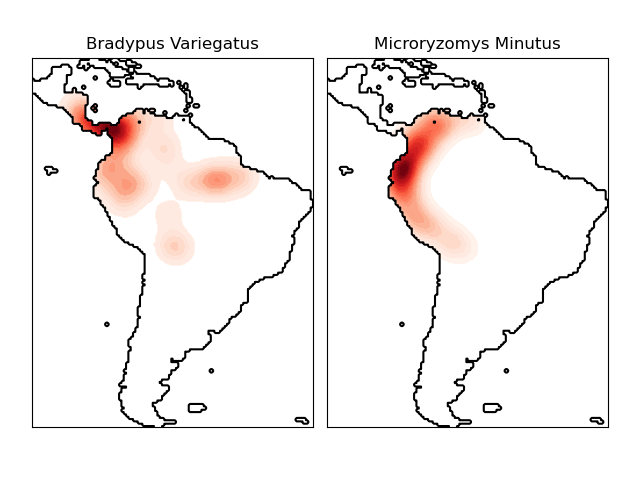
核密度估计器可以与任何有效的距离度量一起使用（有关可用度量的列表，请参见~sklearn.metrics.DistanceMetric），尽管仅对于欧氏距离，结果才正确归一化。一种特别有用的度量是Haversine距离，它测量球面上两点之间的角距离。下面是使用核密度估计对地理空间数据进行可视化的示例，这里是南美洲大陆上两个不同物种的观测分布：

核密度估计的另一个有用应用是学习数据集的非参数生成模型，以便从该生成模型中高效地绘制新样本。下面是使用这个过程在数据的PCA投影上学习高斯核并创建一组新的手写数字的示例：

“新”数据由输入数据的线性组合组成，权重是根据KDE模型概率地绘制的。

示例：

• sphx_glr_auto_examples_neighbors_plot_kde_1d.py：在一维中计算简单的核密度估计。
• sphx_glr_auto_examples_neighbors_plot_digits_kde_sampling.py：使用核密度估计学习手写数字数据的生成模型，并从该模型中绘制新样本的示例。
• sphx_glr_auto_examples_neighbors_plot_species_kde.py：使用Haversine距离度量来可视化地理空间数据的核密度估计的示例。