1.8 线性变换介绍（第1章线性代数中的线性方程组）

最新推荐文章于 2023-08-27 14:54:45 发布

泰克尼客

最新推荐文章于 2023-08-27 14:54:45 发布

阅读量993

点赞数 1

分类专栏：线性代数及其应用系列笔记文章标签：数学线性代数机器学习线性变换矩阵

本文链接：https://blog.csdn.net/wo94chunjie/article/details/103089021

版权

线性代数及其应用系列笔记专栏收录该内容

22 篇文章 59 订阅

订阅专栏

内容概述

本节先从矩阵方程引入了向量变换的一系列概念，接着以矩阵变换为例，探讨了引入向量变换概念后，一些思考问题的新角度以及和之前章节一些概念的结合。最后，由矩阵变换的性质引入了一类比较重要的变换：线性变换，并探讨了线性变换的性质和几个线性变换的例子。需要注意的是，之前学习的线性组合的概念是针对同一空间的向量而言的，而这里线性变换的概念则是针对不同空间的向量而言的。

变换的概念

矩阵方程 $A\boldsymbol x = \boldsymbol b$ ：
在线性代数中的应用不仅仅是直接与向量的线性组合问题有关，通常的情况是把矩阵 $A$ 当作一种对象，它通过乘法“作用”于向量 $\boldsymbol x$ ，产生的新向量称为 $A\boldsymbol x$ 。
例：
参考下面的方程 $A\boldsymbol x = \boldsymbol b$ ：
$\begin{bmatrix}4 & -3 & 1 & 3 \\ 2 & 0 & 5 & 1\end{bmatrix}\begin{bmatrix}1 \\ 1 \\ 1 \\ 1\end{bmatrix} = \begin{bmatrix}5 \\ 8\end{bmatrix}$
和下面的方程 $A\boldsymbol u = \boldsymbol 0$ ：
$\begin{bmatrix}4 & -3 & 1 & 3 \\ 2 & 0 & 5 & 1\end{bmatrix}\begin{bmatrix}1 \\ 4 \\ -1 \\ 3\end{bmatrix} = \begin{bmatrix}0 \\ 0\end{bmatrix}$
乘以矩阵 $A$ 后，将 $\boldsymbol x$ 变成 $\boldsymbol b$ ，将 $\boldsymbol u$ 变成 $\boldsymbol 0$
在这里插入图片描述
由这个新观点，解方程 $A\boldsymbol x = \boldsymbol b$ 就是要求出 $\mathbb R^4$ 中所有经过乘以 $A$ 的“作用”后，变为 $\mathbb R^2$ 中 $\boldsymbol b$ 的向量的 $\boldsymbol x$ 。

由 $\boldsymbol x$ 到 $A\boldsymbol x$ 对应由一个向量集到另一个向量集的函数。这个概念推广了通常的函数概念。

由 $\mathbb R^n$ 到 $\mathbb R^m$ 的一个变换 $\boldsymbol T$ 是一个规则，它把 $\mathbb R^n$ 中每个向量 $\boldsymbol x$ 对应以 $\mathbb R^m$ 中的一个向量 $\boldsymbol T(\boldsymbol x)$ 。集 $\mathbb R^n$ 称为 $\boldsymbol T$ 的定义域，而 $\mathbb R^m$ 称为 $\boldsymbol T$ 的余定义域。符号 $\boldsymbol T: \mathbb R^n \rightarrow \mathbb R^m$ 说明 $\boldsymbol T$ 的定义域是 $\mathbb R^n$ 而余定义域是 $\mathbb R^m$ 。对于 $\mathbb R^n$ 中的向量 $\boldsymbol x$ ， $\mathbb R^m$ 中向量 $\boldsymbol T(\boldsymbol x)$ 称为 $\boldsymbol x$ （在 $\boldsymbol T$ 作用下）的像。所有像 $\boldsymbol T(\boldsymbol x)$ 的集合称为 $\boldsymbol T$ 的值域。
在这里插入图片描述
这里要注意余定义域和值域的区别：

余定义域仅仅说明了定义域中 $\boldsymbol x$ 的像存在于哪个空间，而值域则说明了 $\boldsymbol x$ 的像的具体的取值范围。从这个意义上来说，值域一定是余定义域的子集。

这里引入了向量变换的重要概念，至于变换的类型和性质，则由下文继续深入。

矩阵变换

对于一个 $\times n$ 的矩阵 $A$ ，将矩阵变换 $A\boldsymbol x$ 记为 $\boldsymbol x \rightarrow A\boldsymbol x$ 。需要注意的是，根据矩阵运算的法则，上述变换 $\boldsymbol T$ 的定义域为 $\mathbb R^n$ （ $A$ 有 $n$ 列意味着有 $n$ 个未知数，说明 $\boldsymbol x$ 属于 $\mathbb R^n$ ），余定义域为 $\mathbb R^m$ （ $A\boldsymbol x$ 的计算结果可以看成是矩阵 $A$ 各列的线性组合，因此计算出来的结果向量肯定和组成 $A$ 的各列的向量元素个数相等，属于 $\mathbb R^m$ ）， $\boldsymbol T$ 的值域为 $A$ 的列的所有线性组合（从等价的向量方程的角度去看待矩阵方程可以得出这个观点）。
例：
设 $A=\begin{bmatrix}1 & -3 \\ 3 & 5 \\ -1 & 7\end{bmatrix}$ ， $\boldsymbol u=\begin{bmatrix}2 \\ -1\end{bmatrix}$ ， $\boldsymbol b=\begin{bmatrix}3 \\ 2 \\-5\end{bmatrix}$ ， $\boldsymbol c=\begin{bmatrix}3 \\ 2 \\5\end{bmatrix}$ ，定义变换 $\boldsymbol T: \mathbb R^2 \rightarrow \mathbb R^3$ 为 $\boldsymbol T(\boldsymbol x) = A\boldsymbol x$ ，于是：
$\boldsymbol T(\boldsymbol x) = A\boldsymbol x = \begin{bmatrix}1 & -3 \\ 3 & 5 \\ -1 & 7\end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix} = \begin{bmatrix}x_1 - 3x_2 \\ 3x_1 + 5x_2 \\ -x_1 + 7x_2\end{bmatrix}$
a. 求 $\boldsymbol u$ 在变换 $\boldsymbol T$ 下的像 $\boldsymbol T(\boldsymbol x)$
b. 求 $\mathbb R^2$ 中的向量 $\boldsymbol x$ ，使它在 $\boldsymbol T$ 下的像是 $\boldsymbol b$
c. 是否有其他向量在 $\boldsymbol T$ 下的像也是 $\boldsymbol b$ ？
d. 确定 $\boldsymbol c$ 是否属于变换 $\boldsymbol T$ 的值域。
解：
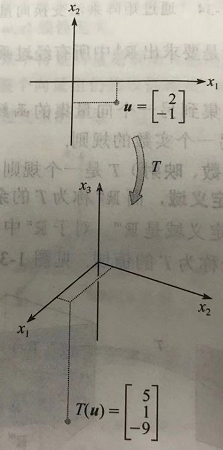
a. 通过计算，可得 $\boldsymbol T(\boldsymbol u) = \begin{bmatrix}5 \\ 1 \\ 9\end{bmatrix}$ ，也就是说，变换 $\boldsymbol T$ 将 $\mathbb R^2$ 中的向量 $\boldsymbol u$ 变换为了 $\mathbb R^3$ 中的另一个向量。如图所示：
在这里插入图片描述
b. 本质就是要求解矩阵方程 $A\boldsymbol x = \boldsymbol b$ ，增广行化简得到：
$\begin{bmatrix}1 & 0 & 1.5 \\ 0 & 1 & -0.5 \\ 0 & 0 & 0 \end{bmatrix}$
易知，向量 $\boldsymbol x = \begin{bmatrix}1.5 \\ -0.5\end{bmatrix}$ 在 $\boldsymbol T$ 下的像是给定的向量 $\boldsymbol b$ 。
c. 由上述增广矩阵的形式可以看出，方程的解是唯一的，所以仅有一个 $\boldsymbol x$ 使它的像是 $\boldsymbol b$ 。
d. 问题表达的是：对某个 $\boldsymbol x$ ， $\boldsymbol c = \boldsymbol T(\boldsymbol x)$ ，也就是说，方程组 $A\boldsymbol x = \boldsymbol c$ 是否相容。将对应的增广矩阵进行行化简后得：
$\begin{bmatrix}1 & -3 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & -35 \end{bmatrix}$
明显的，该方程组不相容，因此 $\boldsymbol c$ 不属于 $\boldsymbol T$ 的值域（但根据定义， $\boldsymbol c$ 仍属于 $\boldsymbol T$ 的余定义域， $\boldsymbol T$ 的余定义域为 $\mathbb R^3$ ）。

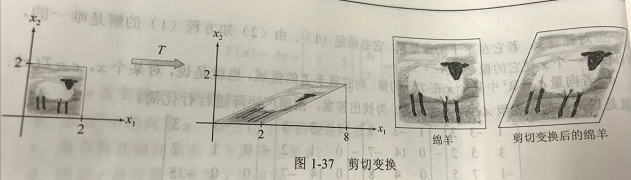
下面是矩阵变换的几个例子，可以从图形学的角度感受下矩阵变换的作用：
在这里插入图片描述

线性变换

1.4节引入了如下定理：

若 $A$ 是 $\times n$ 矩阵，则变换 $\boldsymbol x \rightarrow A\boldsymbol x$ 有以下性质：
$A(\boldsymbol u + \boldsymbol v) = A\boldsymbol u + A\boldsymbol v$
$A(c\boldsymbol u) = cA\boldsymbol u$

参考矩阵的上述性质，引入线性代数中最重要的一类变换：
定义：

变换（或映射） $\boldsymbol T$ 称为线性的，若：
a. 对 $\boldsymbol T$ 的定义域中一切 $\boldsymbol u$ ， $\boldsymbol v$ ， $\boldsymbol T(\boldsymbol u + \boldsymbol v) = \boldsymbol T(\boldsymbol u) + \boldsymbol T(\boldsymbol v)$
b. 对 $\boldsymbol T$ 的定义域中一切 $\boldsymbol u$ 和数 $c$ ， $\boldsymbol T(c\boldsymbol u) = c\boldsymbol T(\boldsymbol u)$

显然，每个矩阵变换都是线性变换（下面一节将说明，所有的线性变换都是矩阵变换）。
上述性质(a)说明，先将 $\mathbb R^n$ 中的 $\boldsymbol u$ 和 $\boldsymbol v$ 相加然后再作用以 $\boldsymbol T$ 的结果 $\boldsymbol T(\boldsymbol u + \boldsymbol v)$ 等于先把 $\boldsymbol T$ 作用于 $\boldsymbol u$ 和 $\boldsymbol v$ 然后将 $\mathbb R^m$ 中的 $\boldsymbol T(\boldsymbol u)$ 和 $\boldsymbol T(\boldsymbol v)$ 相加。
由上述性质又可以推出如下的性质：

若 $\boldsymbol T$ 是线性变换，则：
$\boldsymbol T(\boldsymbol 0) = \boldsymbol 0$
且对 $\boldsymbol T$ 的定义域中一切向量 $\boldsymbol u$ 和 $\boldsymbol v$ 以及数 $c$ 和 $d$ 有：
$\boldsymbol T(c\boldsymbol u + d\boldsymbol v) = c\boldsymbol T(\boldsymbol u) + d\boldsymbol T(\boldsymbol v)$

证明如下：

$\boldsymbol T(\boldsymbol 0) = \boldsymbol T(0 \cdot \boldsymbol0) = 0\boldsymbol T(\boldsymbol 0) = \boldsymbol 0$
$\boldsymbol T(c\boldsymbol u + d\boldsymbol v) = \boldsymbol T(c\boldsymbol u) + \boldsymbol T(d\boldsymbol v) = c\boldsymbol T(u) + d\boldsymbol T(v)$

并且，对于所有 $\boldsymbol u$ ， $\boldsymbol v$ 和 $c$ ， $d$ ，若一个变换满足 $\boldsymbol T(c\boldsymbol u + d\boldsymbol v) = c\boldsymbol T(\boldsymbol u) + d\boldsymbol T(\boldsymbol v)$ ，它必是线性的（取 $c = d = 1$ 可得 $\boldsymbol T(\boldsymbol u + \boldsymbol v) = \boldsymbol T(\boldsymbol u) + \boldsymbol T(\boldsymbol v)$ ），取 $d = 0$ 可得 $\boldsymbol T(c\boldsymbol u) = c\boldsymbol T(\boldsymbol u)$
可以推广到大于两个向量的向量集的情况：
$\boldsymbol T(c_1\boldsymbol v_1 + \cdots + c_p\boldsymbol v_p) = c_1\boldsymbol T(\boldsymbol v_1) + \cdots + c_p\boldsymbol T(\boldsymbol v_p)$
上式称为叠加原理。设想 $\boldsymbol v_1,\boldsymbol v_2,\cdots,\boldsymbol v_p$ 为进入某个系统的信号， $\boldsymbol T(\boldsymbol v_1),\boldsymbol T(\boldsymbol v_2),\cdots,\boldsymbol T(\boldsymbol v_p)$ 为系统对这些信号的响应。系统满足叠加原理，若某一输入可表示为这些信号的线性组合，则系统的响应是对各个信号的响应的同样的线性组合。
例：

给定实数 $r$ ，定义 $\boldsymbol T: \mathbb R^2 \rightarrow \mathbb R^2$ 为 $\boldsymbol T(\boldsymbol x) = r\boldsymbol x$ 。设 $r = 3$ ，证明 $\boldsymbol T$ 是线性变换。

解：

设 $\boldsymbol u$ ， $\boldsymbol v$ 属于 $\mathbb R^2$ ， $c$ , $d$ 为数，则有：
$\boldsymbol T(c\boldsymbol u + d\boldsymbol v)=3(c\boldsymbol u + d\boldsymbol v) = 3c\boldsymbol u + 3d \boldsymbol v=c(3\boldsymbol u) + d(3 \boldsymbol v)=c\boldsymbol T(\boldsymbol u) + d\boldsymbol T(\boldsymbol v)$
因此， $\boldsymbol T$ 是线性变换。

事实上，当 $\leq r \leq 1$ 时， $\boldsymbol T$ 称为压缩变换，当 $r > 1$ 时， $\boldsymbol T$ 称为拉伸变换。
在这里插入图片描述
例：

下图是 $\boldsymbol u = \begin{bmatrix}4 \\ 1\end{bmatrix}$ ， $\boldsymbol v = \begin{bmatrix}2 \\ 3\end{bmatrix}$ ，和 $\boldsymbol v + \boldsymbol v = \begin{bmatrix}6 \\ 4\end{bmatrix}$ 在 $\boldsymbol T = A = \begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix}$ 下的像：

这里可以从几何意义上分别看到该变换的意义（（这是一个从 $\mathbb R^2$ 到 $\mathbb R^2$ 的线性变换，因此可以用同一个坐标系来描述，这个变换让 $\mathbb R^2$ 中的向量逆时针旋转90°）逆时针旋转90°）以及变换的性质（ $\boldsymbol T(\boldsymbol u + \boldsymbol v) = \boldsymbol T(\boldsymbol u) + \boldsymbol T(\boldsymbol v)$ ）

泰克尼客

关注

1
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
1.8 线性变换介绍（第1章线性代数中的线性方程组）

内容概述本节先从矩阵方程引入了向量变换的一系列概念，接着以矩阵变换为例，探讨了引入向量变换概念后，一些思考问题的新角度以及和之前章节一些概念的结合。最后，由矩阵变换的性质引入了一类比较重要的变换：线性变换，并探讨了线性变换的性质和几个线性变换的例子。变换的概念矩阵方程Ax=bA\boldsymbol x = \boldsymbol bAx=b：在线性代数中的应用不仅仅是直接与向量的线性组合...
复制链接

扫一扫