一种改进的粒子群优化算法，原理详解，MATLAB代码免费获取

本期推荐一种改进的粒子群算法，并与原始的粒子群算法(PSO)，灰狼算法(GWO)、北方苍鹰算法(NGO)，鲸鱼算法(WOA)算法进行比较，不得不说，效果确实不错！

粒子群优化算法（PSO）是一种备受关注的元启发式算法，在求解多种优化问题时具有优异的性能。然而，粒子群优化算法面临着收敛速度慢和陷入局部最优的两个主要问题。此外，该算法在高维问题上的性能显著下降。在经典的粒子群算法中，粒子在每次迭代中的移动速度可以是较慢的，也可以是较快的。

最近，一种新的速度暂停粒子群算法（Velocity pausing particle swarm optimization，VPPSO）被提出，在该算法中，粒子在第三种运动方式的支持下，以与前一次迭代相同的速度运动。因此，VPPSO在平衡勘探和开发方面具有更大的潜力。

该算法于2024年发表在计算机领域3区SCI期刊“Neural Computing and Applications”上。

1、算法原理

（1）基础粒子群优化原理

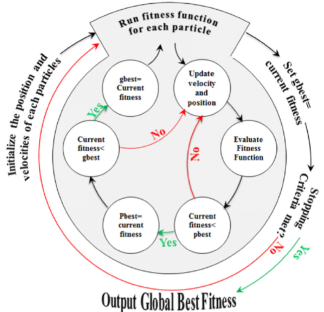
PSO是由Kennedy和Eberhart提出的，其机制受到鸟类群集和鱼类鱼群的社会行为的启发。在粒子群算法中，一群粒子在搜索空间中飞行以寻求最优解。在d维空间中，群中的每个粒子i都有一个位置和一个速度，其数学公式表示如下:

式中，Vi和Xi分别为粒子i的速度矢量和位置矢量，D为维数，N为群体大小。在粒子群优化过程开始时，每个粒子的速度和位置在特定范围内随机生成。在粒子群迭代过程中，粒子i由全局最佳粒子(gbest=[gbest1;gbest2，...，gbestD])，这是迄今为止发现的最好的粒子，也是它的最佳位置(Pbest=[Pbest1，Pbest2，...，phbestD])分别更新其速度和位置，公式如下所示:

其中w为惯性权重，c1和c2分别为认知加速系数和社会加速系数，r1和r2为两个均匀分布在[0,1]范围内的随机变量。惯性权值w的作用是为了避免标准粒子群算法所面临的速度爆炸问题。加速度系数c1和c2分别控制粒子向Pbest和gbest的速度。这三个PSO参数(w, c1和c2)在平衡PSO勘探和开发能力方面起着至关重要的作用。下式是PSO算法的核心，也是开发新型PSO变体所需要的最基本的公式。

粒子更新速度和位置后，其个人最佳位置更新如下:

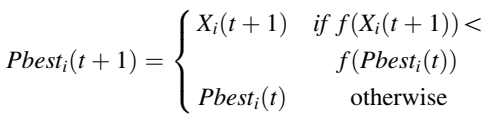
在下式中，只有当新生成的粒子Xi的适应度优于Pbesti的当前适应度时，才会更新粒子i的个人最佳位置。PSO的下一步是基于以下内容更新gbest:

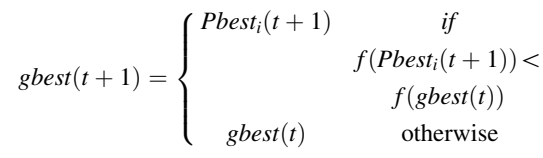
重复PSO过程，直到满足停止条件。

（2）速度暂停粒子群优化

速度暂停是一个新的想法，其中每个粒子不必在每次迭代时更新其速度。换句话说，一个粒子被允许以和它在之前迭代中相同的速度运动。这个想法允许粒子以三种不同的速度移动，即慢速，快速和恒定速度，而不像标准的粒子群算法，粒子只能以更快或更慢的速度移动。速度暂停的主要优点是增加了第三种运动选项(恒定速度)，可以帮助平衡勘探和开采，避免经典PSO的严重过早收敛。速度暂停的概念可以用数学形式表示如下:

式中Vi（t）和Vi（t+1）分别为粒子i在迭代t和t+1时的速度，a为速度暂停参数。当暂停参数a的值大于1时，所有粒子在每次迭代时都会以与经典粒子群算法完全相同的方式更新其速度。这种情况是不希望出现的，因为不会出现速度暂停。另一方面，极低的a值将迫使粒子以恒定的速度移动，并将限制它们以更快或更慢的速度移动。因此，选择最佳的a值来实现平衡的速度暂停场景是至关重要的，这样可以获得最佳性能。为了进一步帮助粒子群算法避免过早收敛，对传统粒子群算法的速度方程进行修改，改变第一速度项，并省略其惯性权重分量，如下所示:

其中a(t)的数学表达式为:

在式中，b是常数。采用速度暂停概念，利用下式中修正的速度方程，VPPSO中的粒子更新其速度如下:

利用该式，将粒子i的位置更新为:

为了保持多样性和避免过早收敛，该算法将种群N分成两个群。第一群由N1个粒子组成，它们根据经典粒子群机制更新自身的速度和位置，不同之处在于:对速度方程的第一项进行修改，并采用速度暂停的概念，如式所示。第二群有N2个粒子，它们只依赖gbest来更新自己的位置。第二群中的每个粒子更新自己的位置如下:

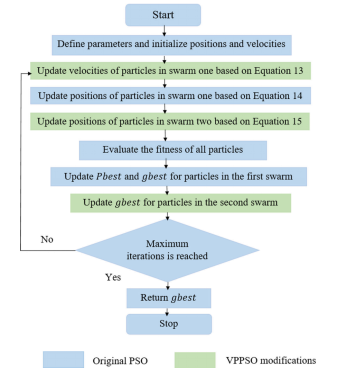
VPPSO的优化过程从随机生成所有粒子的速度和位置开始。在VPPSO迭代过程中，第一群粒子分别根据公式更新速度和位置，第二群粒子根据公式更新位置。VPPSO的下一步是评估所有粒子的适应度。

如果第二群中某个粒子的适应度更好，则在第二群VPPSO中更新全局最优位置。重复VPPSO过程，直到满足停止条件。算法1给出了VPPSO的伪代码。应用算法1对于解决复杂的现实问题，特别是高维问题是非常重要的。算法1引入了速度暂停、新的速度方程和双群策略，更好地平衡了探索和开发，增强了多样性。

所提出的VPPSO算法流程图如图所示。VPPSO的修改用绿色突出显示。该流程图显示了基于新提出的方程更新粒子速度的VPPSO的第一次修改。新速度方程改变了原粒子群速度方程的第一项，避免了速度方程的过早收敛。此外，提出的速度方程实现了速度暂停，以帮助平衡勘探和开采。VPPSO的另一个改进是增加了第二群，其中的粒子以不同的方式更新它们的位置。利用VPPSO的双群策略来提高多样性。对于PSO、VPPSO等现有的元启发式算法，如果gbest向量在迭代t时的适应度优于gbest向量在迭代t时的适应度，则gbest向量在迭代t时被完全替换。

2、结果展示

将本文改进的粒子群算法与原始的粒子群算法(PSO)，灰狼算法(GWO)、北方苍鹰算法(NGO)，鲸鱼算法(WOA)算法进行比较，不得不说，确实效果很好！值得大家学习一下！

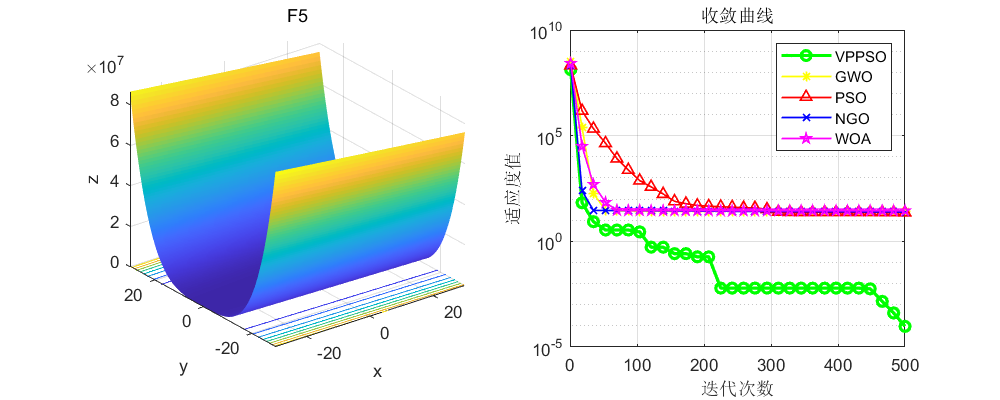
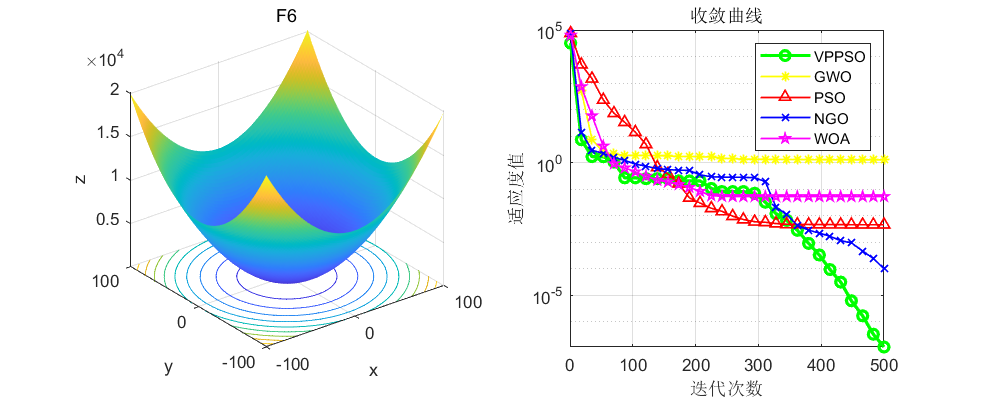
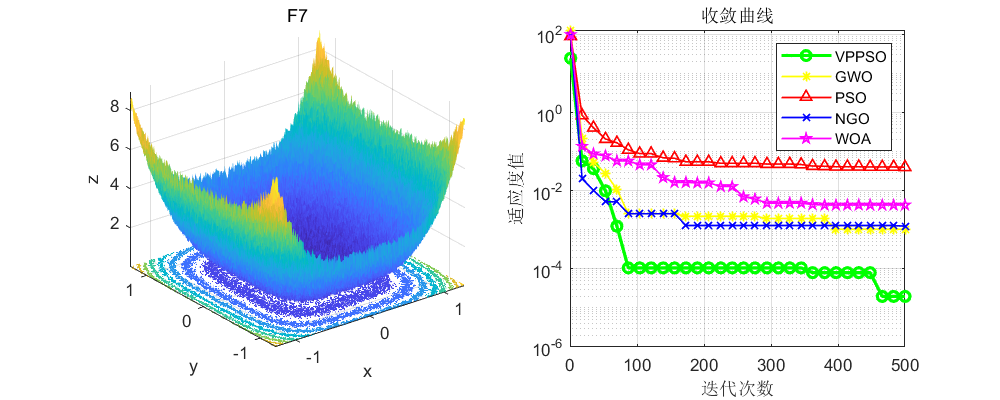
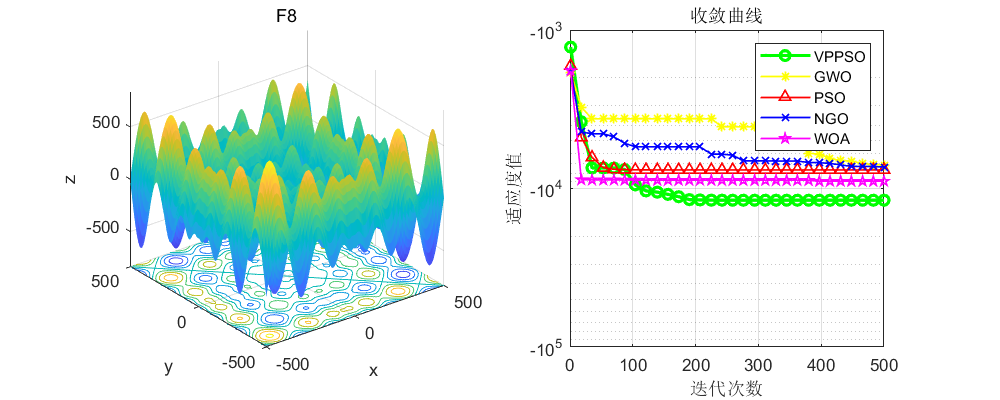
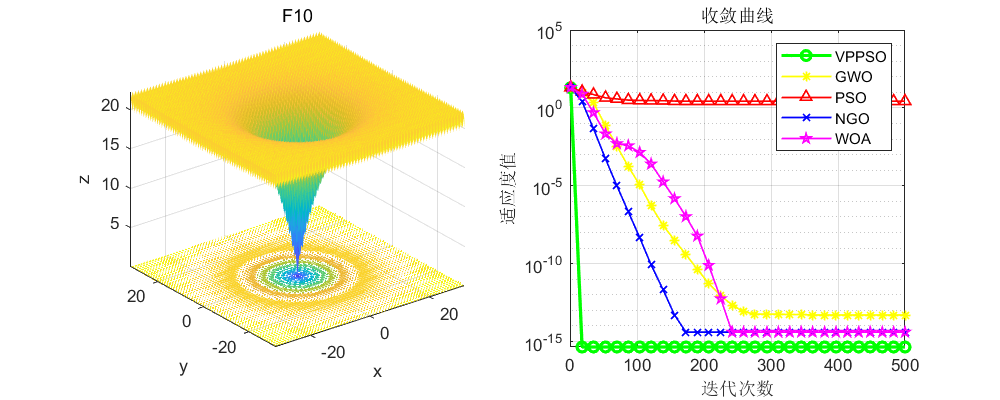
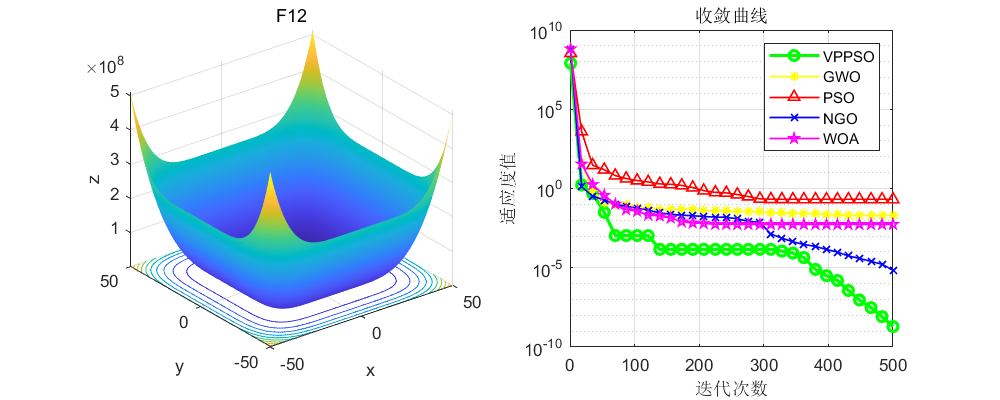
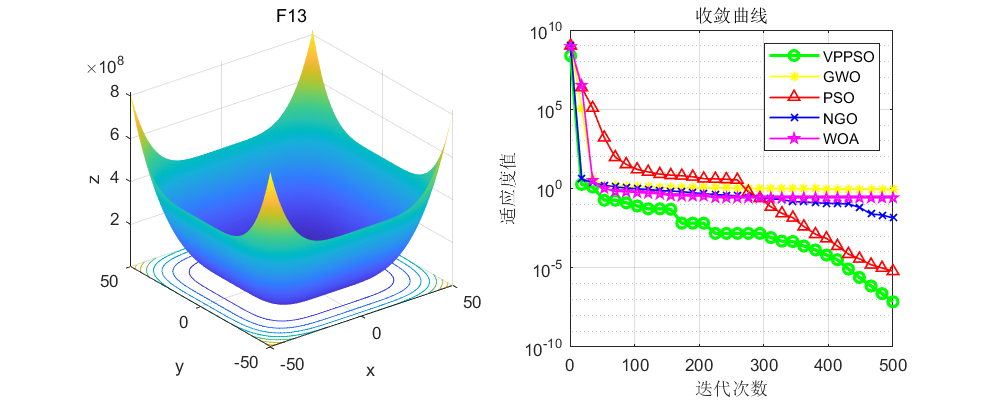
3、MATLAB核心代码

%%
function [gbest_fitness,gbest,Fitness_Curve]= VPPSO(NT,max_iteration,lb,ub,dim,fobj)


lb=lb.*ones(1,dim);
ub=ub.*ones(1,dim);


N = round(NT*0.5);


c1 = 1.5;
c2 = 1.5;


X_min=lb;
X_max=ub;
V_max= ones(1,dim).*(ub-lb).*0.25;           %速度最大值
V_min=-V_max;
gbest_fitness=inf;


%% Intilization
for i=1:N
    Position(i,:)=X_min+(X_max-X_min).*rand(1,dim);
    Velocity(i,:)=zeros(1,dim);


    fitness(i)=fobj(Position(i,:));
    Pbest(i,:)=Position(i,:);
    Pbest_finess(i)= fitness(i);
    if  Pbest_finess(i)<gbest_fitness
        gbest=Pbest(i,:);
        gbest_fitness=Pbest_finess(i);
    end
end


for t=1:max_iteration


    ww(t) =exp(-(2.5*t/max_iteration)^2.5); % Equ. 12
    for i=1:N
        if rand<0.3
            % Equ. 13
            Velocity(i,:)= abs(Velocity(i,:)).^(rand*ww(t))+rand* c1*(Pbest(i,:)-Position(i,:))+rand* c2*(gbest-Position(i,:));
        end
        %% Velociy clamping
        index_Vmax = find(Velocity(i,:)> V_max);
        index_Vmin = find(Velocity(i,:)< V_min);
        %
        Velocity(i, index_Vmax) = V_max(index_Vmax);
        Velocity(i,  index_Vmin) = V_min( index_Vmin);
        Position(i,:)=Position(i,:)+Velocity(i,:);
        %% Boundry check
        index_Pos_ub=find(Position(i,:)> ub);
        index_Pos_lb=find(Position(i,:)< lb);
        Position(i, index_Pos_ub) = ub(index_Pos_ub);
        Position(i,   index_Pos_lb) =lb(  index_Pos_lb);
    end
    %% Second swarm
    for i=N+1:NT


        for j=1:dim


            %% Equ. 15
            CC=ww(t)*rand*abs(gbest(j))^ww(t);
            if rand<0.5
                Position(i,j)=(gbest(j))+ CC;
            else
                Position(i,j)=(gbest(j))- CC;
            end


        end
        %% Boundry check
        index_Pos_ub=find(Position(i,:)> ub);
        index_Pos_lb=find(Position(i,:)< lb);
        Position(i, index_Pos_ub) = ub(index_Pos_ub);
        Position(i, index_Pos_lb) =lb(  index_Pos_lb);
    end


    for i=1:NT
        if i<=N
            %% Evalute fitness
            fitness(i)=fobj(Position(i,:));
            %% Update Pbest
            if fitness(i)< Pbest_finess(i)
                Pbest(i,:)=Position(i,:);
                Pbest_finess(i)=fitness(i);


                if Pbest_finess(i)<gbest_fitness
                    gbest=Pbest(i,:);
                    gbest_fitness=Pbest_finess(i);


                end
            end
        else
            %% Evalute fitness
            fitness(i)=fobj(Position(i,:));
            if  fitness(i)<gbest_fitness
                gbest=Position(i,:);
                gbest_fitness=fitness(i);




            end
        end
    end


    Fitness_Curve(t)= gbest_fitness;


end

参考文献

[1]Shami T M, Mirjalili S, Al-Eryani Y, et al. Velocity pausing particle swarm optimization: A novel variant for global optimization[J]. Neural Computing and Applications, 2023, 35(12): 9193-9223.

完整代码获取

后台回复关键词：

TGDM817

下方卡片关注后获取