Pytorch中scatter与gather操作

wq_0708

已于 2022-03-24 14:30:42 修改

阅读量3.4k

点赞数 6

分类专栏：深度学习文章标签： pytorch 深度学习 python

于 2022-01-10 19:57:14 首次发布

本文链接：https://blog.csdn.net/wq_0708/article/details/122417839

版权

深度学习专栏收录该内容

6 篇文章

订阅专栏

本文详细解析PyTorch中的scatter和gather操作，包括scatter_、scatter_add_及ONNX中的scatterND，阐述它们如何用于张量数据的发散与聚集，并通过实例说明不同约束条件的应用场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数据发散scatter

函数原型pytorch官方文档scatter_：

scatter_(dim, index, src) → Tensor

注： scatter_是scatter的就地操作。

对于一个三维的张量来说，张量self(即调用scatter_的张量)的更新公式如下所示：

self[index[i][j][k]][j][k] = src[i][j][k]  # if dim == 0
self[i][index[i][j][k]][k] = src[i][j][k]  # if dim == 1
self[i][j][index[i][j][k]] = src[i][j][k]  # if dim == 2

其中需要注意的是，scatter对张量self，张量index和张量src之间的维度关系有三个约束：

（1）张量self，张量index和张量src的维度数量必须相同（即三者的.dim()必须相等，注意不是维度大小）；

（2）对于每一个维度d，有index.size(d)<=src.size(d)；

（3）对于每一个维度d，如果d!=dim，有index.size(d)<=self.size(d)；

同时，张量index中的数值大小也有2个约束：

（4）张量index中的每一个值大小必须在[0, self.size(dim)-1]之间；

（5）张量index沿dim维的那一行中所有值都必须是唯一的（弱约束，违反不会报错，但是会造成没有意义的操作）。

其实只要记住scatter的目的是将张量src中的值根据index放入到self中，这几个约束就很好理解，为了进一步方便理解，请看下面的例子：

例1：
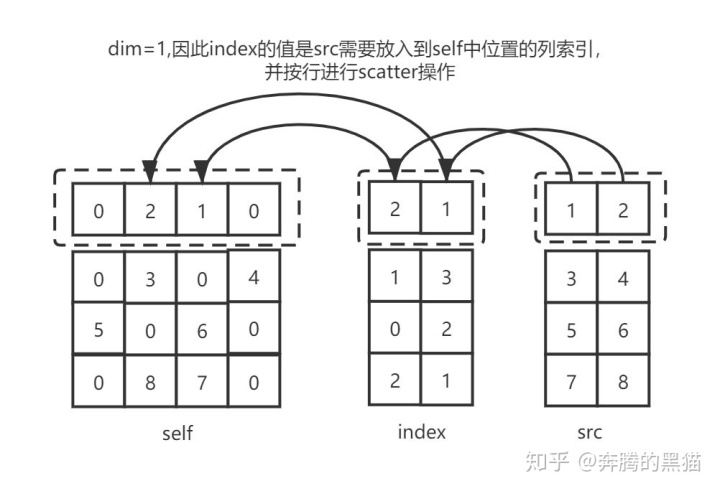
例1.jpg

out = torch.zeros(4, 4)
index = torch.tensor([[2, 1],
                      [1, 3],
                      [0, 2],
                      [2, 1]])
src = torch.tensor([[1, 2],
                    [3, 4],
                    [5, 6],
                    [7, 8]]).float()
res = out.scatter_(1, index, src)
# tensor([[0., 2., 1., 0.],
#         [0., 3., 0., 4.],
#         [5., 0., 6., 0.],
#         [0., 8., 7., 0.]])

例2：

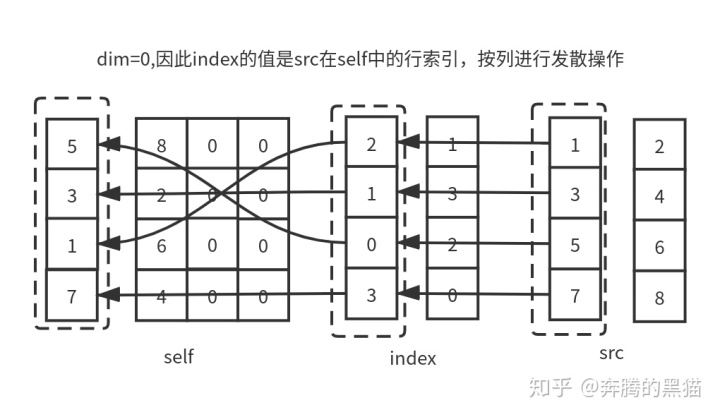
out = torch.zeros(4, 4)
index = torch.tensor([[2, 1],
                      [1, 3],
                      [0, 2],
                      [3, 0]])
src = torch.tensor([[1, 2],
                    [3, 4],
                    [5, 6],
                    [7, 8]]).float()
res = out.scatter_(0, index, src)
# tensor([[5., 8., 0., 0.],
#         [3., 2., 0., 0.],
#         [1., 6., 0., 0.],
#         [7., 4., 0., 0.]])

例3：
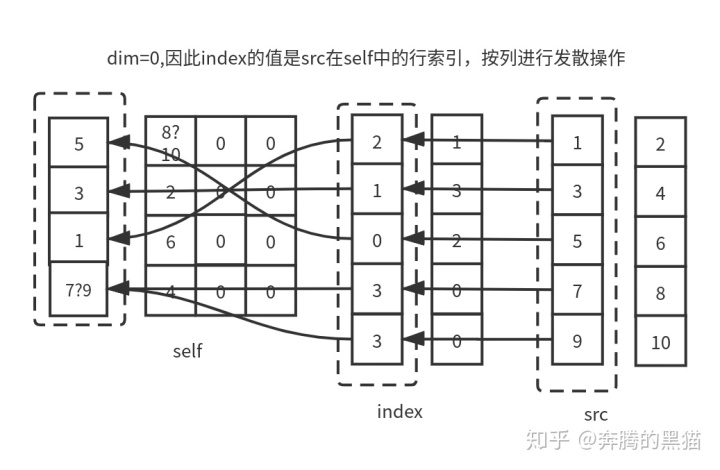
例3.jpg

out = torch.zeros(4, 4)
index = torch.tensor([[2, 1],
                      [1, 3],
                      [0, 2],
                      [3, 0],
                      [3, 0]])
src = torch.tensor([[1, 2],
                    [3, 4],
                    [5, 6],
                    [7, 8],
                    [9, 10]]).float()
res = out.scatter_(0, index, src)
# tensor([[ 5., 10.,  0.,  0.],
#         [ 3.,  2.,  0.,  0.],
#         [ 1.,  6.,  0.,  0.],
#         [ 9.,  4.,  0.,  0.]])

通过3个例子可以理解下约束条件：

约束1： 我们不关心张量self和张量src之间的维度大小关系，他们二者的维度大小之间没有任何关系，我们只需要保证他们维度数量相同即可；

约束2： 因为张量index作为张量src的索引矩阵/向量，其各维度大小必然不可能比src大(因为不可能将一个不存在于src中的值发散到张量self中)

约束3和4： 对于那些d!=dim的维度d来说，其理由和约束2类似（因为不可能将一个src的值发散到一个在张量self中不存在的位置上），而对于那个d==dim的维度来说，index和self之间维度大小没有要求，index.size(dim)可大于self.size(dim)也可小于self.size(dim)，如例3所示。

约束5： 如果index沿着dim维那一行/列中的值不唯一，如例3中，index[3][0]和index[4][0]所示，他们都会将与之对应的src[3][0]和src[4][0]中的值发散到self[3][0]的位置，如果在GPU环境下，具体是src[3][0]还是src[4][0]被放入到了位置self[3][0]是不确定的，因为不能确定是哪一个线程覆盖了另一个线程的值，因此对于操作scatter_来说如果不满足约束5会产生无意义的操作(但不会报错)。

带聚集的发散scatter_add_

上文介绍了scatter_的含义和5个约束条件，下面要介绍的scatter_add_是scatter_的升级版，其基本操作过程和scatter_一模一样，二者唯一的区别就是在我们之前提到的约束5。

scatter_操作的约束5保证了最多只会有一个来自src的值被发散到self的某一个位置上，如果有多于1个的src值被发散到self的同一位置那么会产生无意义的操作。而对于scatter_add_来说，scatter_的前四个约束对其仍然有效，但是scatter_add_没有第5个约束，如果有多于1个的src值被发散到self的同一位置，那么这些值将会通过累加的方式放置到self中。具体如下所示：

例4：

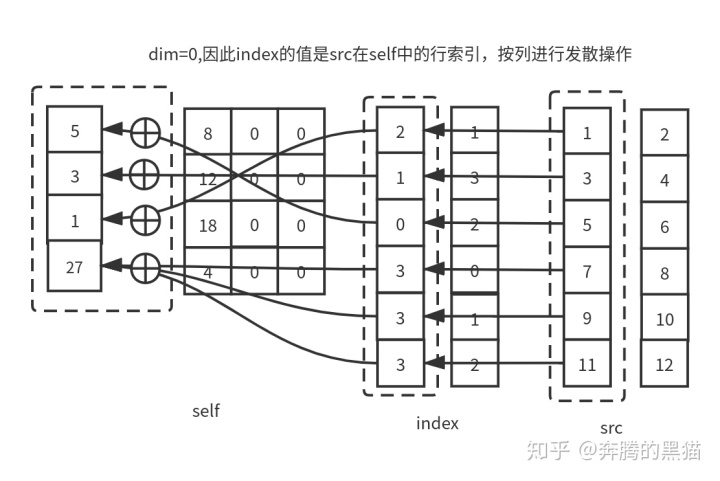
out = torch.zeros(4, 4)
index = torch.tensor([[2, 1],
                      [1, 3],
                      [0, 2],
                      [3, 0],
                      [3, 1],
                      [3, 2]])
src = torch.tensor([[1, 2],
                    [3, 4],
                    [5, 6],
                    [7, 8],
                    [9, 10],
                    [11, 12]]).float()
res = out.scatter_add_(0, index, src)
# tensor([[ 5.,  8.,  0.,  0.],
#         [ 3., 12.,  0.,  0.],
#         [ 1., 18.,  0.,  0.],
#         [27.,  4.,  0.,  0.]])

onnx中scatterND

onnx官方scatterND定义，输入有三个，输出一个

参考onnx——scatterND

import numpy as np

def scatterND(data, indices, updates):
    output = np.copy(data)
    update_indices = indices.shape[:-1]
    for idx in np.ndindex(update_indices):
        output[indices[idx]] = updates[idx]
    return output


if __name__ == "__main__":
    # data = np.array([1, 2, 3, 4, 5, 6, 7, 8])
    # indices = np.array([[4], [3], [1], [7]])
    # updates = np.array([9, 10, 11, 12])

    data = np.array([[[1, 2, 3, 4], [5, 6, 7, 8], [8, 7, 6, 5], [4, 3, 2, 1]],
            [[1, 2, 3, 4], [5, 6, 7, 8], [8, 7, 6, 5], [4, 3, 2, 1]],
            [[8, 7, 6, 5], [4, 3, 2, 1], [1, 2, 3, 4], [5, 6, 7, 8]],
            [[8, 7, 6, 5], [4, 3, 2, 1], [1, 2, 3, 4], [5, 6, 7, 8]]])
    indices = np.array([[0], [2]])
    updates = np.array([[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
               [[1, 1, 1, 1], [2, 2, 2, 2], [3, 3, 3, 3], [4, 4, 4, 4]]])

    out = scatterND(data, indices, updates)
    print(out)

数据聚集gather

函数原型torch.gather：

torch.gather(input,dim,index,out=None,sparse_grad=False)→ Tensor

gather操作是scatter操作的逆操作，如果说scatter是根据index和src求self(input)，那么gather操作是根据self(input)和index求src。具体来说gather操作是根据index指出的索引，沿dim指定的轴收集input的值。

对于一个三维张量来说，gather函数的输出公式为：

out[i][j][k] = input[index[i][j][k]][j][k]  # if dim == 0
out[i][j][k] = input[i][index[i][j][k]][k]  # if dim == 1
out[i][j][k] = input[i][j][index[i][j][k]]  # if dim == 2

对于gather操作来说，也有三个约束需要满足：

（1）对于所有的维度d != dim，有input.size(d) == index.size(d)，对于维度d==dim来说，有index.size(d) >= 1；

（2）张量out的维度大小必须和index相同；

（3）和scatter一样，index中的索引值必须在input.size(dim)范围内。

例5（和例1对照）：

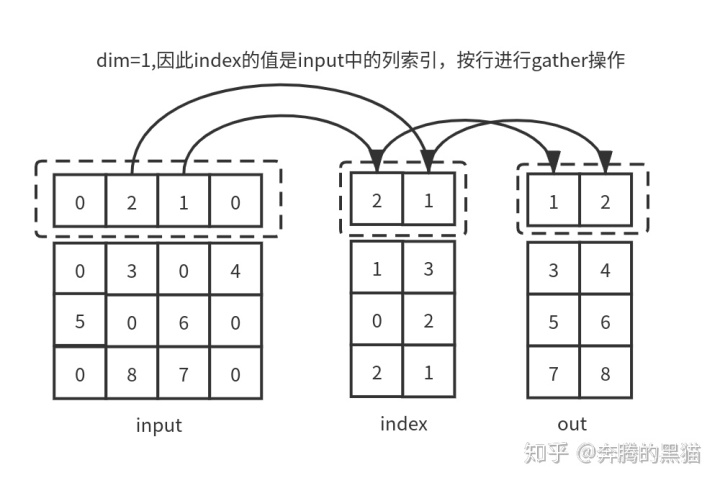
inp = torch.tensor([[0, 2, 1, 0],
                    [0, 3, 0, 4],
                    [5, 0, 6, 0],
                    [0, 8, 7, 0]])
index = torch.tensor([[2, 1],
                      [1, 3],
                      [0, 2],
                      [2, 1]])
res = inp.gather(1, index)
# tensor([[1, 2],
#         [3, 4],
#         [5, 6],
#         [7, 8]])

例6（和例3对照）：

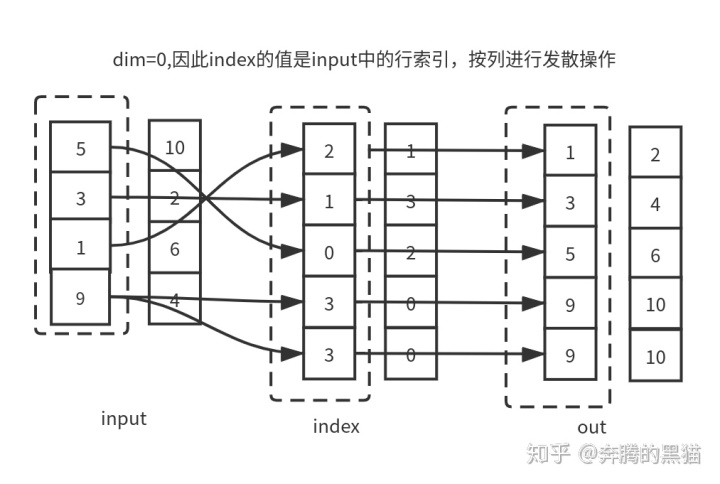
注：图中“发散”打错了，应为“聚集”

inp = torch.tensor([[5, 10],
                    [3, 2],
                    [1, 6],
                    [9, 4]])
index = torch.tensor([[2, 1],
                      [1, 3],
                      [0, 2],
                      [3, 0],
                      [3, 0]])
res = inp.gather(0, index)
# tensor([[ 1,  2],
#         [ 3,  4],
#         [ 5,  6],
#         [ 9, 10],
#         [ 9, 10]])