g2o学习——g2o整体框架

写在前面

进来对g2o优化库进行了学习，虽然才模仿着写了两个例程，但是对于整个g2o的理解和使用方面还是多了不少的感触，特此写下博客，对这些天的学习进行记录。

g2o的整体结构

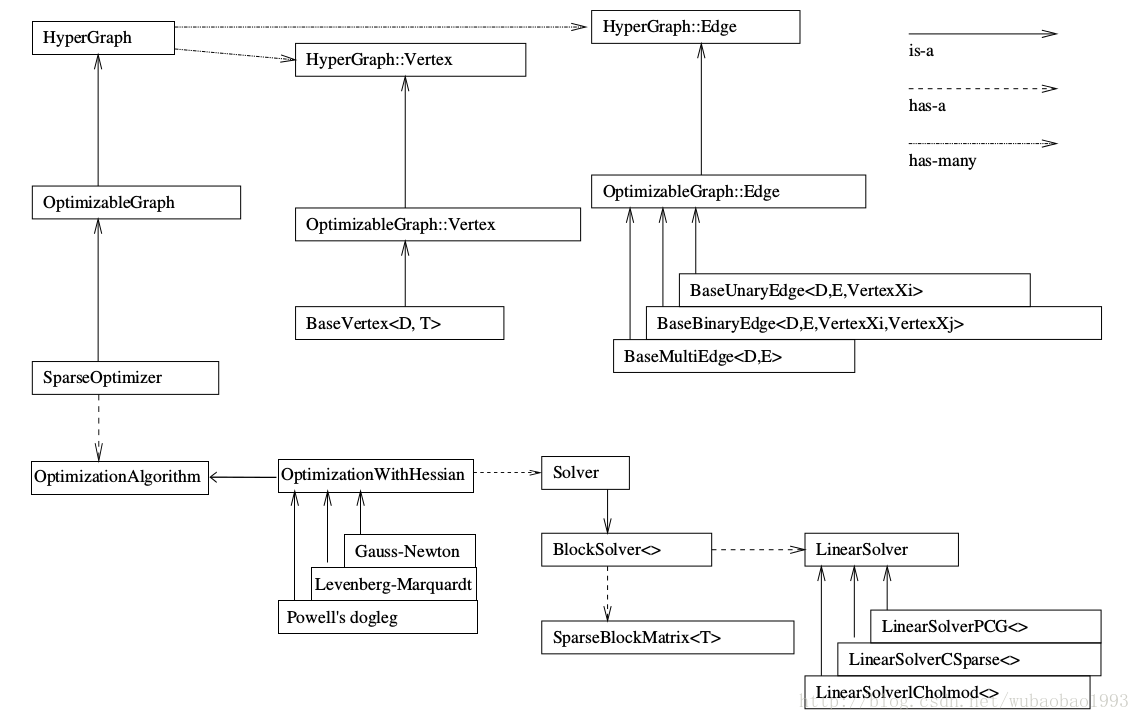
说到整体的结构，不得不用一张比较概括的图来说明：

这张图最好跟着画一下，这样能更好的理解和掌握，例如我第一次看的时候根本没有注意说箭头的类型等等的细节。

那么从图中我们其实比较容易的就看出来整个库里面较为重要的类之间的继承以及包含关系，也可以看出整个框架里面最重要的东西就是SparseOptimizer这个类（或者说实例）。

顶点（Vertex）和边（Edge）

顺着图往上看，可以看到我们所使用的优化器最终是一个超图（hyperGrahp），而这个超图包含了许多顶点（Vertex）和边（Edge）。这两个类型是我们在看程序和写程序中比较关注的东西了，g2o不像Ceres，内部很多东西其实作者都已经写好了（此刻一鞠躬），很适合我们这些新兴的懒惰青年，但是同时，我们也失去了一个比较完整的了解内部关系的机会，不过这个东西我们可以通过看内部的实现补回来（但是编程实践是没有机会了），顺便看看大牛写的代码～

那么扯回来，在图优化中，顶点代表了要被优化的变量，而边则是连接被优化变量的桥梁，因此，也就造成了说我们在程序中见得较多的就是这两种类型的初始化和赋值。

在整个优化过程中，顶点的值会越来越趋近于最有值，优化完毕后则可以将顶点的优化值作为最优值进行使用；边则是连接顶点的类型，在SLAM问题中，一般是边连接要被优化的空间点（Point）和机器人的位姿（Pose），当然，边还可以连接一个顶点（类似与参数估计，边的数量由量测的数量决定），也可以连接多个顶点（超图，这里笔者还没有遇到过，就不妄言了），边在图优化中的一个很大的作用就是计算误差（视觉SLAM中计算的就是空间点的映射误差），同时计算该误差对于被优化变量的jacobian矩阵，也是比较重要的存在。

自定义顶点（Vertex）和边（Edge）

我们在用g2o的时候，不会一帆风顺的就能适合自身机器人的实际情况，总会遇到自己独特的顶点类型和边类型，此时我们需要对顶点和边进行重写，那么重写也比较简单，这里简单进行记录。

在整体框架图中，可以看到不管是顶点还是边，都可以说是继承自baseXXX这个类的，因此我们在自定义的时候，也可以仿照着继承这两个类，当然也可以继承自g2o中较为“成熟”的类，不管怎样，都要重写下述的函数。

自定义顶点

virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void oplusImpl(const number_t* update);
virtual void setToOriginImpl();

其中read，write函数可以不进行覆写，仅仅声明一下就可以，setToOriginImpl设定被优化变量的原始值，oplusImpl比较重要，我们根据增量方程计算出增量之后，就是通过这个函数对估计值进行调整的，因此这个函数的内容一定要写对，否则会造成一直优化却得不到好的优化结果的现象。

自定义边

virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void computeError();
virtual void linearizeOplus();

read和write函数同上，computeError函数是使用当前顶点的值计算的测量值与真实的测量值之间的误差，linearizeOplus函数是在当前顶点的值下，该误差对优化变量的偏导数，即jacobian。

自定义的总结

不管是自定义边还是顶点，除了自己加入的一些变量，还都要对一些g2o框架要调用的函数进行覆写，这些函数用户可以声明为实函数（即不加virtual），但是笔者还是建议声明为虚函数。

优化算法（Algorithm，BlockSolver，linearSolver）

顺着整体结构图往下看，可以看到这部分其实算是整个g2o里面比较隐晦的部分，设计到优化的算法，块求解器，线性求解器等等部分，在程序中，这部分通常位于g2o算法的开头配置部分，一般情况下我们可以随着一个例程进行配置即可，这里对这部分进行了稍微浅显的理解，特意写在这里（下面的东西纯属个人理解了，如有不妥还请大神指出：）。

linearSolver，线性求解器

我们知道在求解增量方程HdeltaX=-b的时候，通常情况下想到线性求解，很简单嘛，deltaX=-H.inv*b，的确，当H的维度较小的时候，上述问题变得简单，只需要矩阵的求逆就能解决问题，但是当H的维度较大时，问题变得复杂，此时我们就需要一些特殊的方法对矩阵进行求逆，g2o中主要有图中所示的三种方法，PCG，CSparse和Cholmod方法。

注意，这里说再多，线性求解器仅仅只是完成了一个求解的功能，可以说是整个优化中比较靠后的计算部分了。

BlockSolver，块求解器（参数块求解器？）

块求解器是包含线性求解器的存在，之所以是包含，是因为块求解器会构建好线性求解器所需要的矩阵块（也就是H和b），之后给线性求解器让它进行运算，边的jacobian也就是在这个时候发挥了自己的光和热。

这里再记录下一个比较容易混淆的问题，也就是在初始化块求解器的时候的参数问题。

大部分的例程在初始化块求解器的时候都会使用如下的程序代码：

std::unique_ptr<g2o::BlockSolver_6_3::LinearSolverType> linearSolver = g2o::make_unique<g2o::LinearSolverCholmod<g2o::BlockSolver_6_3::PoseMatrixType>>();

其中的BlockSolver_6_3有两个参数，分别是6和3，在定义的时候可以看到这是一个模板的重命名（模板类的重命名只能用using）

template<int p, int l>
using BlockSolverPL = BlockSolver< BlockSolverTraits<p, l> >;

其中p代表pose的维度，l表示landmark的维度，且这里都表示的是增量的维度（这里笔者也不是很确定，但是从后续的程序中可以看出是增量的维度而并非是状态变量的维度）。

因此（后面的话以SLAM情况为例），对于仅仅优化位姿的应用而言，这里l的值是没有太大影响的，因为H矩阵中并没有Hll的块，因此这里的维度也就没有用武之地了。

Algorithm，优化算法

这里就不多讲了，从图中可以看到主要有三种方法：GN，LM，PSD，不同的方法主要表现在最终的H矩阵构造不同。

总结

1. 对g2o优化库的整体框架有了更好的了解

2. 对图中的顶点和边有了更加深刻的认识

3. 理解了g2o初始化部分的程序与意图

以上观点仅仅代表个人学习观点，如有不对还请各位大神指正！这里不胜感激！