定积分在几何学上的应用

最新推荐文章于 2024-05-06 19:24:54 发布

宝哥大数据

最新推荐文章于 2024-05-06 19:24:54 发布

阅读量5k

点赞数 3

分类专栏：数学基础及计算机理论 # 高数

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/wuxintdrh/article/details/104711310

版权

数学基础及计算机理论同时被 2 个专栏收录

67 篇文章

订阅专栏

44 篇文章

订阅专栏

一、平面图像的面积

1.1、直角坐标

1.1.1、例1：积分变量选取不同

如果选取x为积分变量，面积元素分成两部分，增加计算量
在这里插入图片描述

1.1.2、参数方程

在这里插入图片描述

1.2、极坐标

在这里插入图片描述

1.2.1、例

在这里插入图片描述

二、体积

2.1、旋转体的体积

2.1.1、绕x轴

在这里插入图片描述

2.1.2、绕y轴

在这里插入图片描述

2.1.3、例

在这里插入图片描述

2.2、平行截面面积为已知的立体的体积

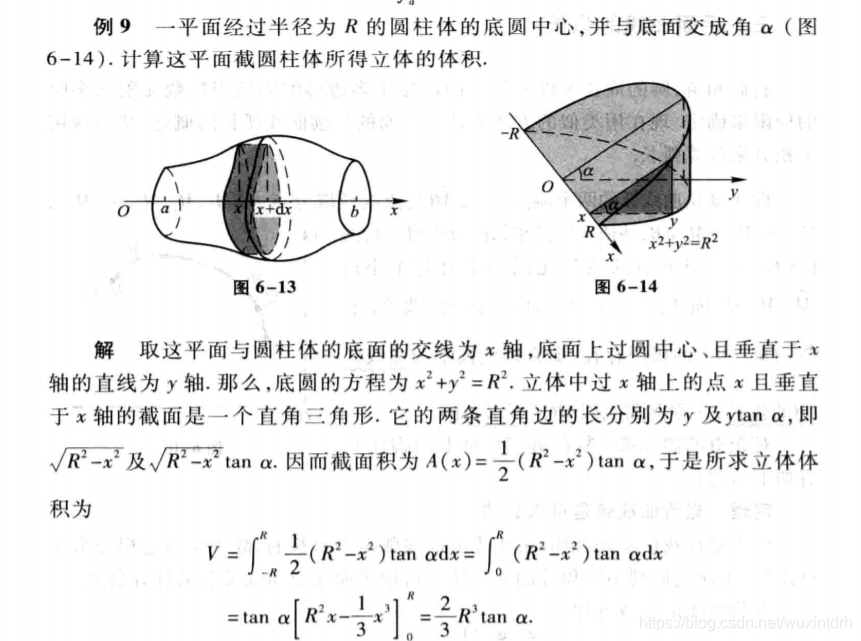
在这里插入图片描述

2.2.1、例1

在这里插入图片描述

2.2.2、例2

在这里插入图片描述

三、平面曲线弧长

弧微分

3.1、光滑曲线弧是可求长的

在这里插入图片描述

3.1.1、参数方程下的曲线弧

在这里插入图片描述

3.1.2、直角坐标下的曲线弧

在这里插入图片描述

3.1.3、极坐标下的曲线弧

在这里插入图片描述

3.2、例题

3.2.1、例1

在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。