1、什么是线性代数
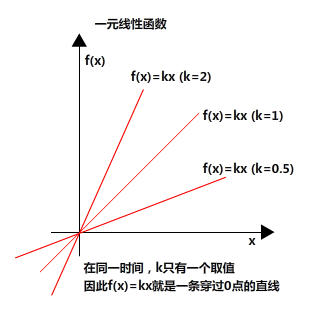
(1)什么是一元线性函数:
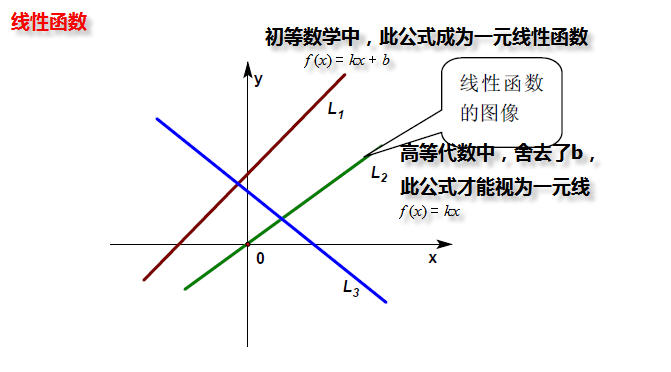
(2)线性的代数意义
线性最基本意义有两条:
<1>可加性(和的函数等于函数的和):
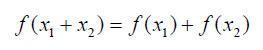
<2>比例性,也叫齐次性、数乘性或均匀性(比例的函数等于函数的比例,或说自变量缩放,函数也同比例地缩放)
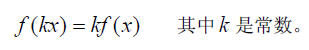
注意,f(x) = kx+b不满足比例性,因此带b的就不称为线性函数了。
总结:两条结合成一条:
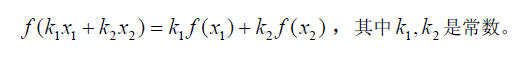
线性组合的函数,等于函数的线性组合。
(3)n元线性齐次函数
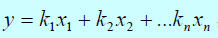
(4)n元线性方程组
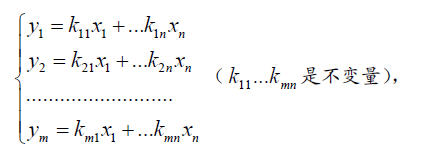
如果m=n,那么这个方程组所确立的图形也是一条直线;如果m!=n则图形是平面或超平面的,平面是多线性的。
改写为:
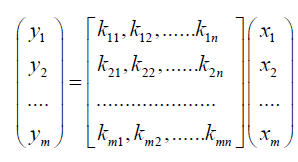
进一步简写:
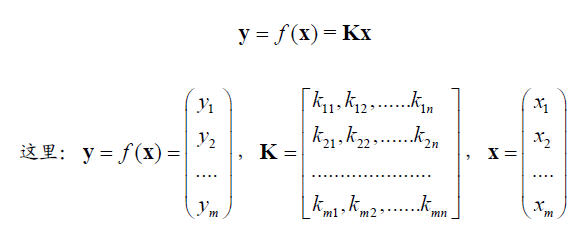
(5)一元线性的几何意义
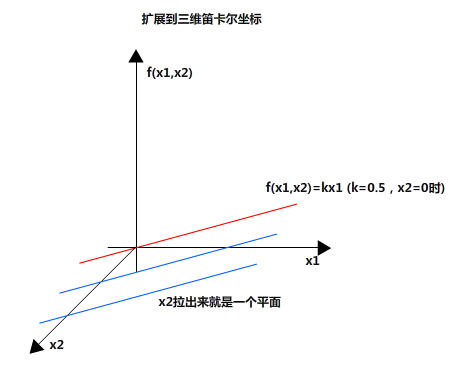
(6)扩展到三维笛卡尔坐标
(7)两个平面在三维笛卡尔坐标
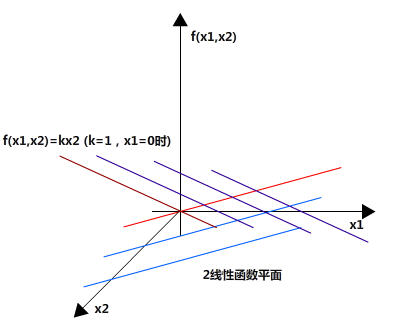
注意此2个线性函数平面,一个是往x1方向生长,一个是往x2方向生长
(8)把函数改为映射关系
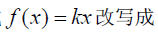
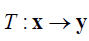 一个从自变量的集合x到因变量的集合y的映射
一个从自变量的集合x到因变量的集合y的映射
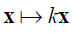 两个集合里的自变量x到因变量y之间的具体的对应变换关系
两个集合里的自变量x到因变量y之间的具体的对应变换关系
(9)集合示意图1
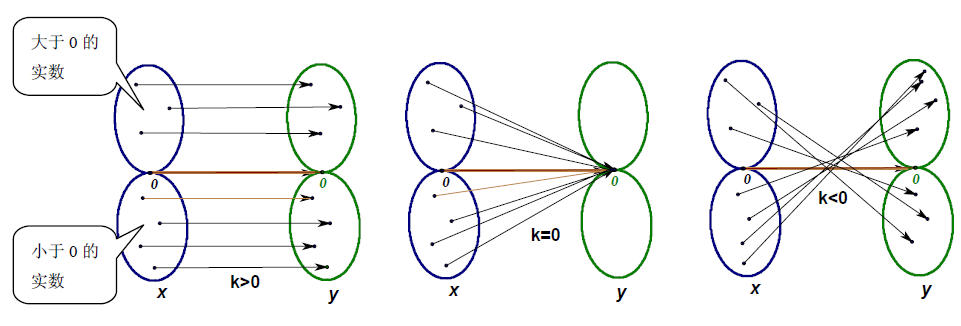
(10)集合示意图2
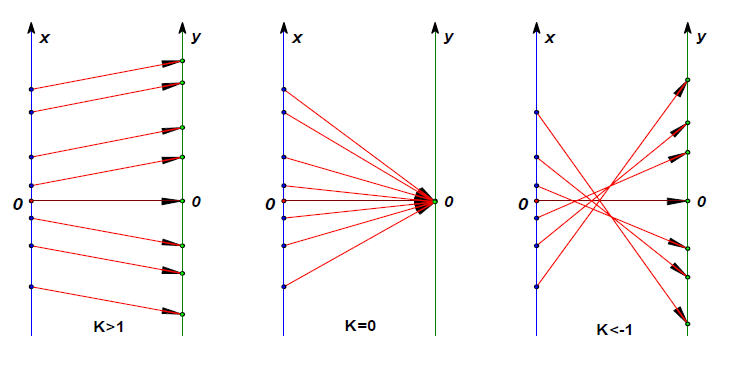
(11)映射到笛卡尔坐标
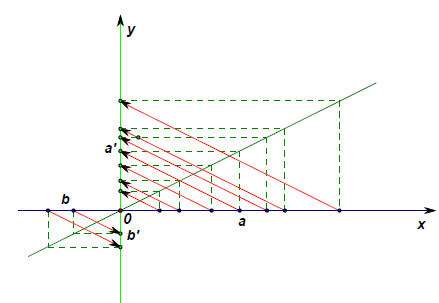
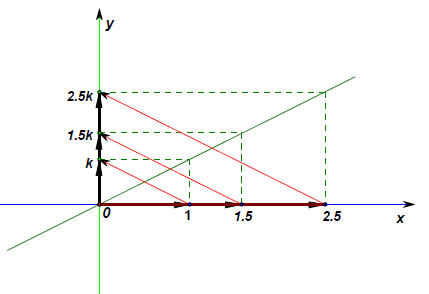
线性映射,就是线段映射到线段!
(12)把x1、x2想象为一个平面,把y1,y2想象为一个平面
函数式:
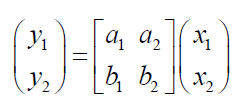
y1 = a1x1+a2x2;
y2 = b1x1+b2x2
k值:
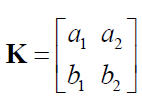
映射关系:
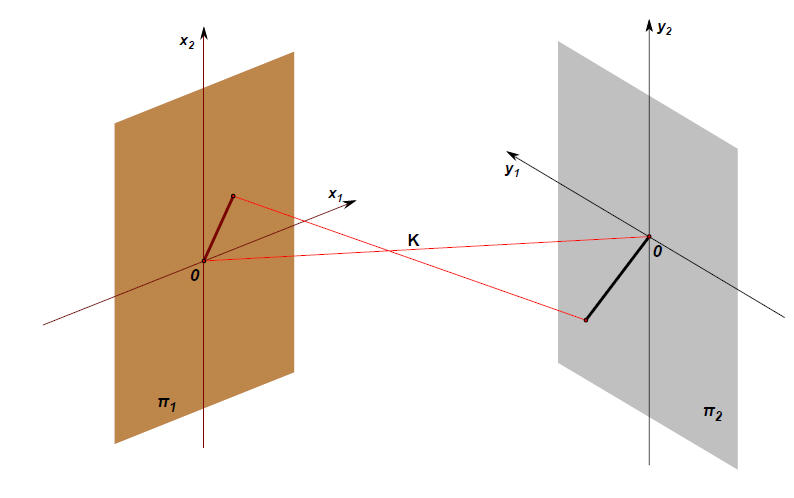
(13)把上面的两个平面做垂直放置
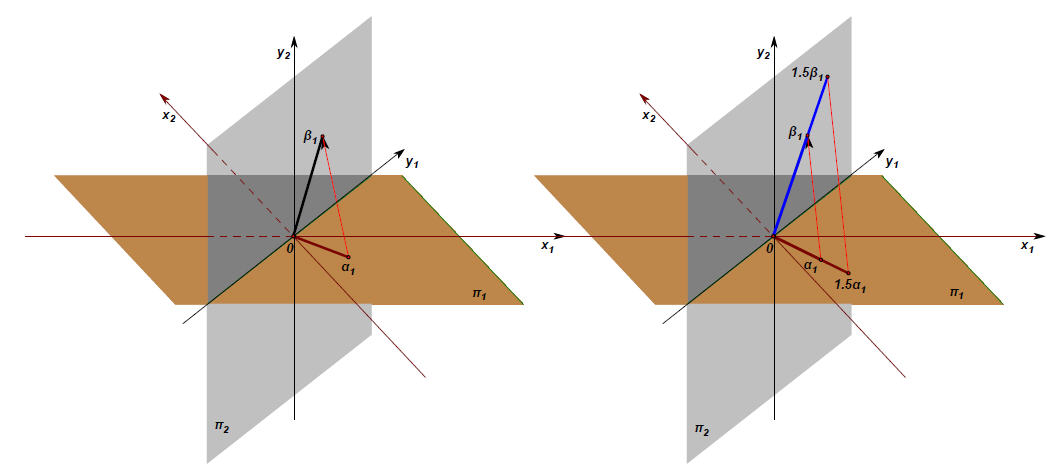
























 1327
1327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








