谱定理是线性代数中很重要很基础的定理,并为以后的特征值分解做准备
1 谱定理
设A是nxn复矩阵,则复数域上任意向量都可以写成A的特征向量之和,其中特征向量可以是广义特征向量.
谱定理的证明需要以下引理或推论
2 引理1
设p,q是两个复系数多项式,并且没有公共零点,则存在另外两个
多项式a,b使得:
证明:
以下证明只是简述,并不是严格证明:
假设形如qp+bq次数最低的非零多项式记做d,易证d整除p和q
又根据p,q无公共零点,因此易证d是常数,假设:
即证明了该引理.
3 引理2
设p,q为无公共零点的多项式,A是复数域上的方阵,则:
即任意x属于Npq可以唯一的分解
证明:
对推论1中的自变量为A有:
等式两端同时作用在x上得到:
由于同一矩阵的多项式可交换,并且x属于p(A)q(A)的零空间:
因此证明了推论
(并没有证明分解的唯一性,,,)
4 推论:
设p1,p2,...,pk是一簇多项式,任意两个无公共零点N1,...,Nk分别是他们的零空间,则:
该推论的证明略
5 证明谱定理
任取向量x,则n+1个向量x,Ax,...,A^nx必定线性相关,即存在次数不大于n的多项式p:
对p进行分解:
其中Rj是p的根,Mj是Rj的重数,如果Rj不是A的特征值则A-RjI可逆.
将可逆因子移到前端,剩下的Rj是A的特征值.若记:
则(2)式可重写为:
显然任意两个Pj无公共零点,则由推论10,x可分解为Npj中向量之和.
由(3)式和广义特征向量定义知任意x属于Npj都是A的广义特征向量,
这样就将x分解为A的广义特征向量之和。定理得证








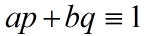
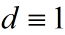

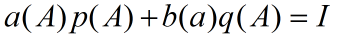

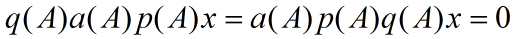
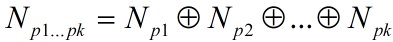
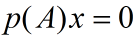

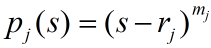
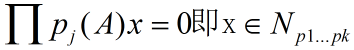














 1083
1083











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








