【游戏开发3D数学笔记】4.矩阵和线性变换

一.不同变换的矩阵推导

• 旋转

在前文知道旋转矩阵的行向量就是旋转后的坐标系的基向量。2D中绕原点的旋转只有一个参数，角度θ，它描述了旋转量。逆时针旋转经常（不是必须）被认为是正方向，顺时针方向是负方向。如下图，我们很容易得到旋转后的基向量，从而得到旋转矩阵：

2D旋转矩阵

$R(\theta) = \begin{bmatrix}{p'} \\ {q'}\end{bmatrix} = \begin{bmatrix}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$

在3D中，绕坐标轴旋转，而不是绕点旋转，此时首先需要定义的是何为旋转正方向：         左手坐标系中定义此方向的规则为左手法则。首先，要明确旋转轴指向哪个方向。当然，旋转轴在理论上是无限延伸的，但我们还是要认为它有正端点和负端点。与笛卡尔坐标轴定义坐标系相同，左手法则是这样的:伸出左手，大拇指向上，其余手指弯曲。大拇指指向旋转轴的正方向，此时，四指弯曲的方向就是旋转的正方向。如下图：

下面是分别以$x,y,z$轴旋转$\theta$角度的旋转矩阵：(矩阵行向量是变换后的坐标系的基向量)

3D旋转矩阵

$x轴: {R_x}(\theta)=\begin{bmatrix}1&0&0 \\ 0&cos\theta&sin\theta \\ 0&-sin\theta&cos\theta\end{bmatrix} y轴: {R_y}(\theta)=\begin{bmatrix}cos\theta&0&-sin\theta \\ 0&1&0 \\ sin\theta&0&cos\theta\end{bmatrix} z轴: {R_z}(\theta)=\begin{bmatrix}cos\theta&-sin\theta&0 \\ -sin\theta&cos\theta&0 \\ 0&0&1\end{bmatrix}$

在3D中还可以绕任意轴的旋转。因为不考虑平移，这里的轴一定是通过原点的。这里我们不给与证明，需要看数学证明的可以看这里，下面给出旋转矩阵：($我们令n为旋转轴,\theta为旋转角度$)

3D绕任意轴旋转矩阵

${R(n,\theta)}=\begin{bmatrix}p'\\q'\\r'\end{bmatrix}=\begin{bmatrix}{n_x}^2(1-cos\theta)+cos\theta&{n_x}{n_y}(1-cos\theta)+{n_z}sin\theta&{n_x}{n_z}(1-cos\theta)-{n_y}sin\theta \\ {n_x}{n_y}(1-cos\theta)-{n_z}sin\theta&{n_y}^2(1-cos\theta)+cos\theta&{n_y}{n_z}(1-cos\theta)+{n_x}sin\theta \\ {n_x}{n_z}(1-cos\theta)+{n_y}sin\theta&{n_y}{n_z}(1-cos\theta)-{n_x}sin\theta&{n_z}^2(1-cos\theta)+cos\theta\end{bmatrix}$

---

• 缩放

我们可以通过让比例因子k按比例放大或缩小来缩放物体。如果在各方向应用同比例的缩放，并且沿原点“膨胀”物体，那么就是均匀缩放。均匀缩放可以保 持物体的角度和比例不变。如果长度增加或减小因子k，则面积增加或减小k^2。在3D中，体积将增加或减小 k^3。         如果需要“挤压”或”拉伸”物体，在不同的方向应用不同的因子即可，这称作非均匀缩放。非均匀缩放时，物体角度将发生变化。视各方向缩放因子的不 同，长度、面积、体积的变化因子也各不相同。         如果|k|<1，物体将“变短”；如果|k|>1，物体将“变长”，如果k = 0，就是正交投影，如果k < 0就是镜像。应用非均匀缩放的效果类似于切变，事实上，非均匀缩放和切变和很难区分的。

沿坐标轴缩放矩阵

$2D : \quad S({k_x},{k_y})= \begin{bmatrix}p'\\q'\end{bmatrix}=\begin{bmatrix}{k_x}&0\\0&{k_y}\end{bmatrix}\quad\quad3D: \quad S({k_x},{k_y},{k_z})= \begin{bmatrix}p'\\q'\\r'\end{bmatrix}=\begin{bmatrix}{k_x}&0&0\\0&{k_y}&0\\0&0&{k_z}\end{bmatrix}$

同样，沿着任意方向的缩放要更加复杂一点，不过我们还是可以通过将原向量按照缩放方向分解成沿着缩放方向和垂直缩放方向，然后只需要缩放沿着缩放方向的分支然后再合成。如下图：

具体的证明可以参照此处：这里，最后缩放矩阵如下：

沿任意轴缩放矩阵

$2D : \quad S(n,k)= \begin{bmatrix}p'\\q'\end{bmatrix}=\begin{bmatrix}1+(k-1){n_x}^2&(k-1){n_x}{n_y}\\(k-1){n_x}{n_y}&1+(k-1){n_y}^2\end{bmatrix}$

$3D: \quad S(n,k)= \begin{bmatrix}p'\\q'\\r'\end{bmatrix}=\begin{bmatrix}1+(k-1){n_x}^2&(k-1){n_x}{n_y}&(k-1){n_x}{n_z}\\(k-1){n_x}{n_y}&1+(k-1){n_y}^2&(k-1){n_y}{n_z}\\(k-1){n_x}{n_z}&(k-1){n_z}{n_y}&1+(k-1){n_z}^2\end{bmatrix}$

---

• 正交投影

一般来说，投影意味着降维操作，有一种投影方法是在某个方向上用0作为缩放因子。这种情况下，所有点都被拉平至垂直的轴（2D）或平面（3D）上。 这种类型的投影称作正交投影（或者平行投影），因为从原来的点到投影点的直线相互平行。         通过使垂直方向上的缩放因子为零就能达到正交投影的目的：

沿坐标轴正交投影矩阵

$向x轴投影2D矩阵： {P_x} = S([0\quad 1], 0) =\begin{bmatrix}1&0\\0&0\end{bmatrix}\quad\quad(注明一下：这里的S()上一段的缩放矩阵)$
$向y轴投影2D矩阵： {P_x} = S([1\quad 0], 0) =\begin{bmatrix}0&0\\0&1\end{bmatrix}$

沿坐标平面正交投影矩阵

$向xy平面投影3D矩阵： {P_{xy}} = S([0\quad 0\quad 1], 0) =\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}$
$向xz平面投影3D矩阵： {P_{xz}} = S([0\quad 1\quad 0], 0) =\begin{bmatrix}1&0&0\\0&0&0\\0&0&1\end{bmatrix}$
$向yz平面投影3D矩阵： {P_{yz}} = S([1\quad 0\quad 0], 0) =\begin{bmatrix}0&0&0\\0&1&0\\0&0&1\end{bmatrix}$

向任意直线或者平面投影(n为投影方向)

$向任意线投影2D矩阵： P(n) = S(n, 0) =\begin{bmatrix}1-{n_x}^2&-{n_x}{n_y}\\-{n_x}{n_y}&1-{n_y}^2\end{bmatrix}$
$向任意平面投影3D矩阵： P(n) = S(n, 0) =\begin{bmatrix}1-{n_x}^2&-{n_x}{n_y}&-{n_x}{n_z}\\-{n_x}{n_y}&1-{n_y}^2&-{n_y}{n_z}\\-{n_x}{n_z}&-{n_z}{n_y}&1-{n_z}^2\end{bmatrix}$

---

• 镜像投影

镜像也叫做反射，与正交投影相似，正交投影将缩放值k设为0，而镜像则设为-1。

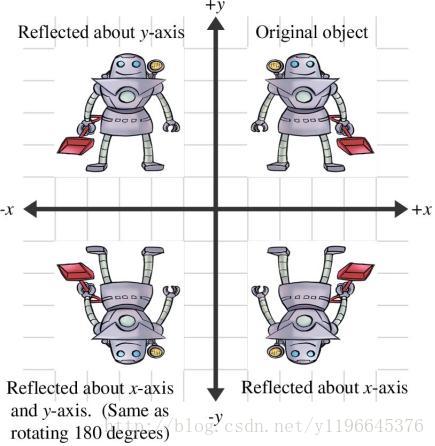
沿任意轴镜像的矩阵(轴过原点)

$2D:\quad\quad P(n) = S(n,-1) = \begin{bmatrix}1-2{n_x}^2&-2{n_x}{n_y}\\-2{n_x}{n_y}&1-2{n_y}^2\end{bmatrix}\quad\quad(注明一下：这里的S()上面的缩放矩阵)$

$3D:\quad\quad P(n) = S(n,-1) = \begin{bmatrix}1-2{n_x}^2&-2{n_x}{n_y}&-2{n_x}{n_z}\\-2{n_x}{n_y}&1-2{n_y}^2&-2{n_y}{n_z}\\-2{n_x}{n_z}&-2{n_z}{n_y}&1-2{n_z}^2\end{bmatrix}$

---

• 切变

。切变是坐标系的变换，非均匀的拉伸。切变时候，角度变化，但是面积或体积不变。也可以理解为坐标轴间的角度变化，造成的扭曲。 如下图，这是x坐标根据y坐标的切变，机器人的y坐标没有变化，只有x坐标变化了，变化后的坐标x’可以理解为将y坐标乘以切变因子s与原坐标x的和：$x'= x + sy$。如果是3D则增加z坐标的切变因子$t： x'= x + sz，y'= y + tz$

切变矩阵

$2D:\quad\quad{H_x}(s) =\begin{bmatrix}1&0\\s&1\end{bmatrix}\quad\quad{H_y}(s)=\begin{bmatrix}1&s\\0&1\end{bmatrix}\quad\quad({H_x}的意义是x坐标根据坐标y被切变，同理{H_y})$

$3D:\quad\quad{H_{xy}}(s) =\begin{bmatrix}1&0&0\\0&1&0\\s&t&1\end{bmatrix}\quad\quad{H_{xz}}(s)=\begin{bmatrix}1&0&0\\s&1&t\\0&0&1\end{bmatrix}\quad\quad{H_{yz}}=\begin{bmatrix}1&s&t\\0&1&0\\0&0&1\end{bmatrix}$

切变是一种很少用到的变换，它也被称作 扭曲变换。 包含切变与缩放（均匀或非均匀）的变换通常很容易与包含旋转与非均匀缩放（只能是非均匀）的变换发生混淆。

---

二.变换的分类

• 1.线性变换

$满足：F(a+b)=F(a)+F(b) \quad以及\quad F(ka)=kF(a)的映射F(a)就是线性的。$

$其实映射F(a)=aM,当M为任意方阵的时候，也可以说明F映射是一个线性变换。$

所以，根据上面的结论我们知道，以上我们提到的变换都是线性变换；但是有一个可能出乎意料的事实：平移不是线性变换。

• 2.仿射变换

$具有v'=vM+b的变换都是仿射变换。$

平移作为最常用的变换之一，然而却不是线性变换；所以为了包括平移变换提出了仿射变换。仿射变换是指线性变换后接着平移。因此，仿射变换的集合是线性变换的超集，任何线性变换都是仿射变换，但不是所有的仿射变换都是线性变换。事实上，可能有的人会觉得平移也可以由一个矩阵变换得到，如下：

$(0,0)\to(1,0) : \quad\quad \begin{bmatrix}x&y&1\end{bmatrix}\begin{bmatrix}1&0&0\\0&1&0\\1&0&1\end{bmatrix} = \begin{bmatrix}x+1&y&1\end{bmatrix}$

当然，这并不意味着平移变换就是线性变换了，事实上：增加一个维度之后，就可以在高维度通过线性变换来完成低维度的仿射变换。对于高维度来说只是经历了一次切变+投影变换就可以实现低维度的平移。查看更多

• 3.可逆变换

如果存在一个逆变换可以”撤销”原变换，那么称这个变换是可逆的。存在非仿射变换的可逆变换，不过暂不考虑它们；我们知道仿射变换是线性变换加上平移，对于平移我们肯定是可以通过相反的量来撤销；所以对于一个仿射变换是否可逆，只需要看它的线性变换是否可逆。         在上面的所有变幻中，除了投影变换，其他变换都能”撤销”。当物体被投影时，某一维度的有用信息被抛弃了，所以这些信息是没法恢复的。

• 4.等角变换

如果变化前后两个向量的夹角大小和方向都不改变，该变换是等角的。         只有平移，旋转和均匀缩放是等角变化，而镜像变换会改变夹角的方向。

• 5.正交变换

正交变换的基本思想是保持轴相互垂直，并且不进行缩放变换。         平移，旋转，镜像是仅有的正交变换。正交变换中：长度、角度、体积、面积都是不会发生改变的！！

• 6.刚体变换

刚体变换是只改变物体的位置和方向，不包括形状。         平移，旋转是仅有的正交变换。所有的刚体变换都是正交、等角、可逆和仿射的！！

三.变换类别的关系

变换	线性	仿射	可逆	等角	正交	刚体	等长	等面积	行列式
线性	Y	Y
仿射		Y
可逆			Y						≠0
等角		Y	Y	Y
正交		Y	Y		Y				$\pm1$
刚体		Y	Y	Y	Y	Y	Y	Y
平移		Y	Y	Y	Y	Y	Y	Y
旋转	Y	Y	Y	Y	Y	Y	Y	Y	1
均匀缩放	Y	Y	Y	Y					$K^N$
非均匀缩放	Y	Y	Y
正交投影	Y	Y							0
镜像	Y	Y	Y		Y		Y	Y	-1
切变	Y	Y	Y					Y	1