稳定的双共轭梯度法(BiCGSTAB)

系数矩阵非对称时，线性方程组如何求解？-稳定双共轭梯度法(Bicgstab)求解线性方程组

在前面的文章和中表明共轭梯度法是求解对称正定线性方程组的一种有效方法，当针对不同的系数矩阵采用不同的预处理方式时，其可以以较少的迭代次数获得较高精度的解。然而，该方法的一个缺点就是其只能适用于对称正定系数矩阵，当系数矩阵不再是对称正定时，此方法可能失效。以下举例：

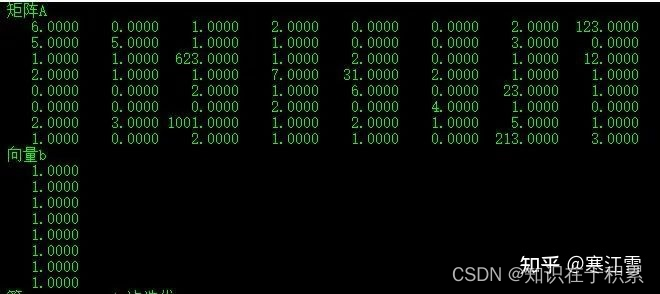
上面矩阵A为非对称矩阵，采用共轭梯度法求解过程如下：

该方程组采用共轭梯度法迭代4862次依然未收敛。因此，对于该非对称方程，可以认为，共轭梯度法几乎是失效的。在实际工程中，有限元方法形成的刚度系数以对称正定居多，但是实际上也存在非对称的可能，例如，当材料本构采用摩尔-库伦本构时，其形成的刚度矩阵就有可能会是非对称的，此时如果是使用商业软件，应当在软件中选择非对称求解器。如果是自主编程且采用迭代法求解线性方程组，则需要找到一种适用于非对称矩阵的求解方法。

常见的非对称系数矩阵求解方法主要有：广义最小残差法(GMRES)，双共轭梯度法（Bicg）稳定双共轭梯度法(BiCGStab)，稳定混合双共轭梯度法（BiCGStab(l)），这些方法相对于常规的共轭梯度法在推导上均增加了一些难度，实际推导往往较为复杂。本文不展开推导，仅对稳定双共轭梯度法(BiCGStab)的伪代码作简要粘贴。BiCGStab法的具体计算过程如下：

program bicgstab_main
    implicit none
    integer,parameter::n=8
    real(8)::a(n,n),b(n)
    real(8)::x(n),x0(n)
    integer::i,j
    integer,parameter::m=20
    real(8)::c(m,m),d(m)
    real(8)::y(m),y0(m)
 
 
    a=reshape((/6,5,1,2,0,0,2,1, &
                0,5,1,1,0,0,3,0,& 
                1,1,623,1,2,0,1001,2, &
                2,1,1,7,1,2,1,1,&
                0,0,2,31,6,0,2,1,&
                0,0,0,2,0,4,1,0,&
                2,3,1,1,23,1,5,213,&
                123,0,12,1,1,0,1,3/),(/n,n/))
    b=(/1,1,1,1,1,1,1,1/)
    write(*,*)"矩阵A"
    write(*,"(8f10.4)")(a(i,:),i=1,n)
    write(*,*)"向量b"
    write(*,"(f10.4)")b
    x0=100.0
    x=0.0
    call bicgstab(a,b,x,x0,n)
    end program bicgstab_main
subroutine bicgstab(a,b,x,x0,n)
    implicit none
    integer,intent(in)::n
    real(kind=8),intent(in)::a(n,n),b(n),x0(n)
    real(kind=8),intent(out)::x(n)
    real(kind=8)::p0(n),r0(n)
    real(kind=8)::tol=1.0d-6
    integer::nmax=1000
    real(kind=8)::rj(n),pj(n)
    real(kind=8)::alphaj
    real(kind=8)::r0_bar(n)
    real(kind=8)::sj(n)
    real(kind=8)::xjp1(n),xj(n)
    real(kind=8)::wj
    real(kind=8)::rjp1(n)
    real(kind=8)::betaj
    integer::n_iter
    real(kind=8)::apj(n),asj(n)
 
    r0=b-matmul(a,x0)
    r0_bar=r0
    if(abs(dot_product(r0,r0_bar))<tol) then
        write(*,*)"unvalid r0_bar,select an other!"
        return    
    endif
    p0=r0
     rj=r0
     pj=p0
     xj=x0
 
     n_iter=0
    do
        if(n_iter>nmax) then
            write(*,*)"exceed max iter!"
            exit
        endif
        alphaj=dot_product(rj,r0_bar)/dot_product(matmul(a,pj),r0_bar)
        apj=matmul(a,pj)
        sj=rj-alphaj*apj
        if(norm2(sj)<tol) then
            xjp1=xj+alphaj*pj
            x=xjp1
            exit
        endif
        asj=matmul(a,sj)
    wj=dot_product(asj,sj)/(norm2(asj))**2
    xjp1=xj+alphaj*pj+wj*sj
    rjp1=sj-wj*asj
 
    if(norm2(rjp1)<tol) then
        x=xjp1
        exit
    endif
    betaj=alphaj*dot_product(rjp1,r0_bar)/(wj*dot_product(rj,r0_bar))
    pj=rjp1+betaj*(pj-wj*apj)
    xj=xjp1
    rj=rjp1
    n_iter=n_iter+1
    write(*,*)"the",n_iter,"iter!"
    enddo
 
    write(*,*)"the solution of equation:"
    write(*,"(es18.8)")x
    end subroutine bicgstab

依据上述过程编写程序，计算前述非对称矩阵线性方程组求解结果：

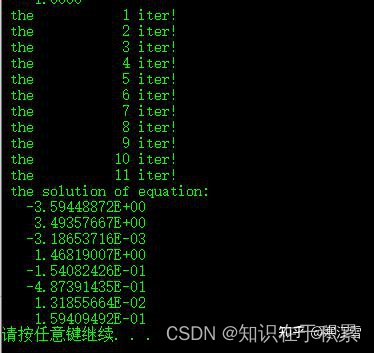
采用matlab求解该方程组的解：

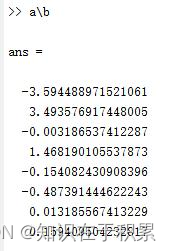
通过对比可知11次迭代已经获得即为准确的结果。实际上，对于该方法也可以通过一定的预处理方式，使得其所需要的迭代次数更少。
https://zhuanlan.zhihu.com/p/537095177

而由维基百科
1、未预处理的

2、预处理后的