vitis HLS中实现求平方根的库函数Sqrt解析

希言自然也

已于 2024-01-25 16:45:32 修改

阅读量1k

点赞数 21

分类专栏： # HLS 文章标签： fpga开发 c++ HLS

于 2024-01-21 13:45:25 首次发布

本文链接：https://blog.csdn.net/yindq1220/article/details/135440305

版权

HLS 专栏收录该内容

6 篇文章 1 订阅

订阅专栏

一、一般实现求平方根的几个算法

1、cordic算法。是一种适合在FPGA中实现多种数学求解的算法，这个可以参考我之前写的文章。

CORDIC算法理论详解-CSDN博客

vivado cordic IP学习记录_xqn格式的数字-CSDN博客

2、二分法

二分法相对来说比较简单，假设我们要求数字y的平方根x。

第1步：我们假设平方根的最大值max，一般为数字y；假设一个平方根的最小值min，一般为0。

第2步：计算 $((max+min)/2)^{2}$ 的结果。

若结果比y小，则根据上一步的max和min的值，更新 $max=(max+min)/2$ ；

若结果比y大，则根据上一步的max和min的值，更新 $min=(max+min)/2$ ；

第N步：循环执行第2步，直到 $((max+min)/2)^{2}$ 与y相等，那么 $(max+min)/2$ 即为平方根x。

举例如下，16的平方根。

①假设max=16，min=0;

②因为(16+0)/2=8；8的平方等于64>16; 此时更新max=8

③因为(8+0)/2=4；4的平方等于16=16；此时即得到平方根为4

（注意的是，上述二分法未考虑数字y<1的情况。并且二分法可能会引入非常多的小数位，不太适合FPGA实现。本文仅涉猎下此算法，不进行深究，有兴趣自行翻阅资料）

3、牛顿迭代法

牛顿迭代法的理论推导，此处不做研究，只给出求平方根时的用法。

牛顿迭代法：求√a 的结果x.

第1步：初始值取x=1。

第2步：m=(x+a/x)/2，即m为x和a/x的平均值。

第3步：x=m，将第2步的结果赋值给x。

重复上面的第2步和第3步.....

......

第N步：直到x和a/x差不多相等，此时x即为平方根的近似值。

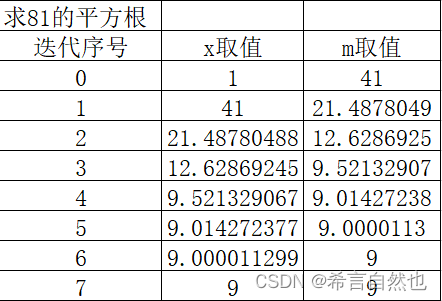
举例如下：

最后81的平方根即为9，结果正确。

（注意：基本上，a的数值越大，需要迭代的次数越多，可以根据经验确定迭代次数）

当然了，上面的算法不是我们要说的重点。本文要说的重点是vitisHLS中的库函数是如何实现求解平方根的。

二、恢复余数除法和不恢复余数除法

可是，先不要着急，这里再多嘴描述一下除法的实现方式，方便后面对平方根计算算法的理解。

除法器的实现（恢复余数、不恢复余数、级数展开、Newton-Raphson）_不恢复余数除法器设计框图-CSDN博客

1、恢复余数除法

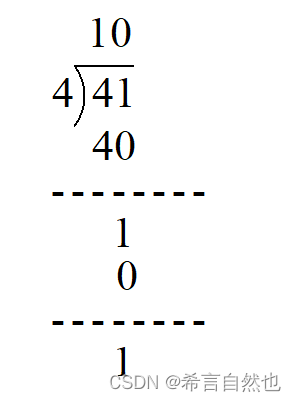
上式子是我们小学时代学习的除法计算方式，41除4的结果是10余1，他实际上就是一种恢复余数除法。基本思想是，余数为负数时，需要将余数的结果加上除数，恢复成原来的余数。

在FPGA中实现恢复余数除法时，全部是以二进制数据处理的，上面十进制的41除4，使用二进制表示如下：

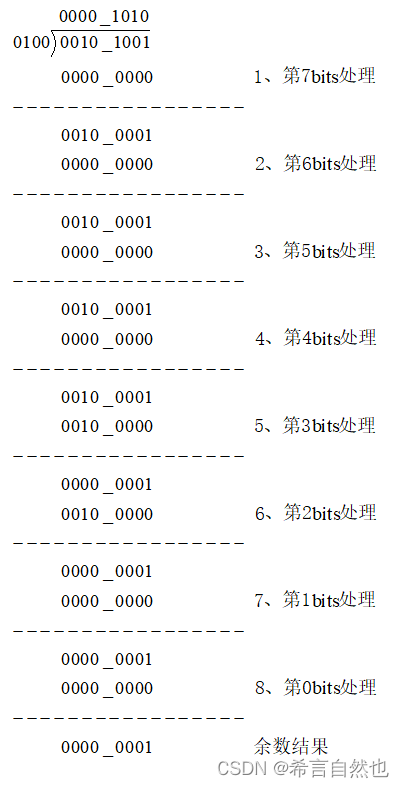
我们先定义：每一步计算出来的余数结果为remainder[i]

被除数：dividend

除数：divisor

每一步计算出来的余数结果为remainder[i]，（remainder[0]=dividend）

每一步对应的商的bit结果为quotient[j]

此时对于恢复余数法，我们有以下公式remainder[i] = remainder[i-1] - divisor*quotient[j]*2^j 。由于对于二进制来说，商的bit位上，只能是1或者0。列出流程图如下：

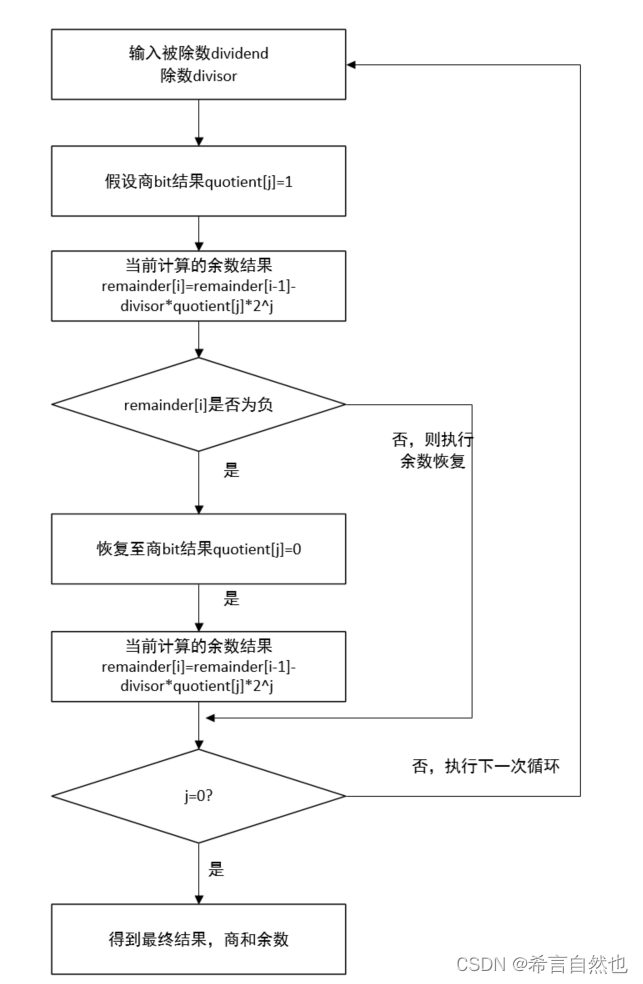
41除4进行示例演练，所以我们有如下计算：

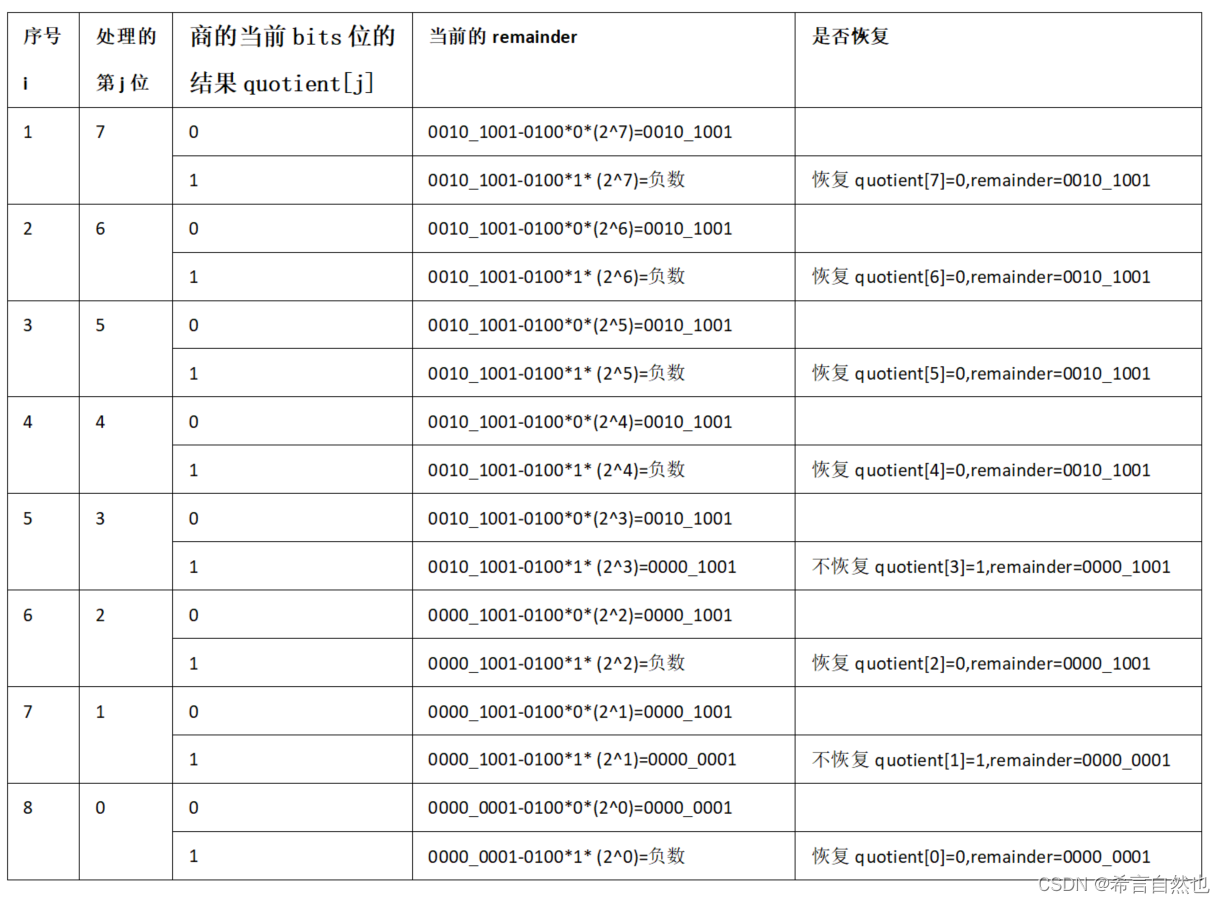
上面的除法计算思路，就是恢复余数除法。当然，实际工程中，添加个if判断即可，不需要多增加运算时钟进行数据恢复。

2、不恢复余数除法

不恢复余数除法是对应着恢复余数除法来说的，核心是不再将数据进行恢复，而是在下一次运算时，更改remainder[i] = remainder[i-1]+D*quotient[j]*2^j的运算符号，由加法变为减法或者减法变加法，进行结果修正。流程图表示如下：

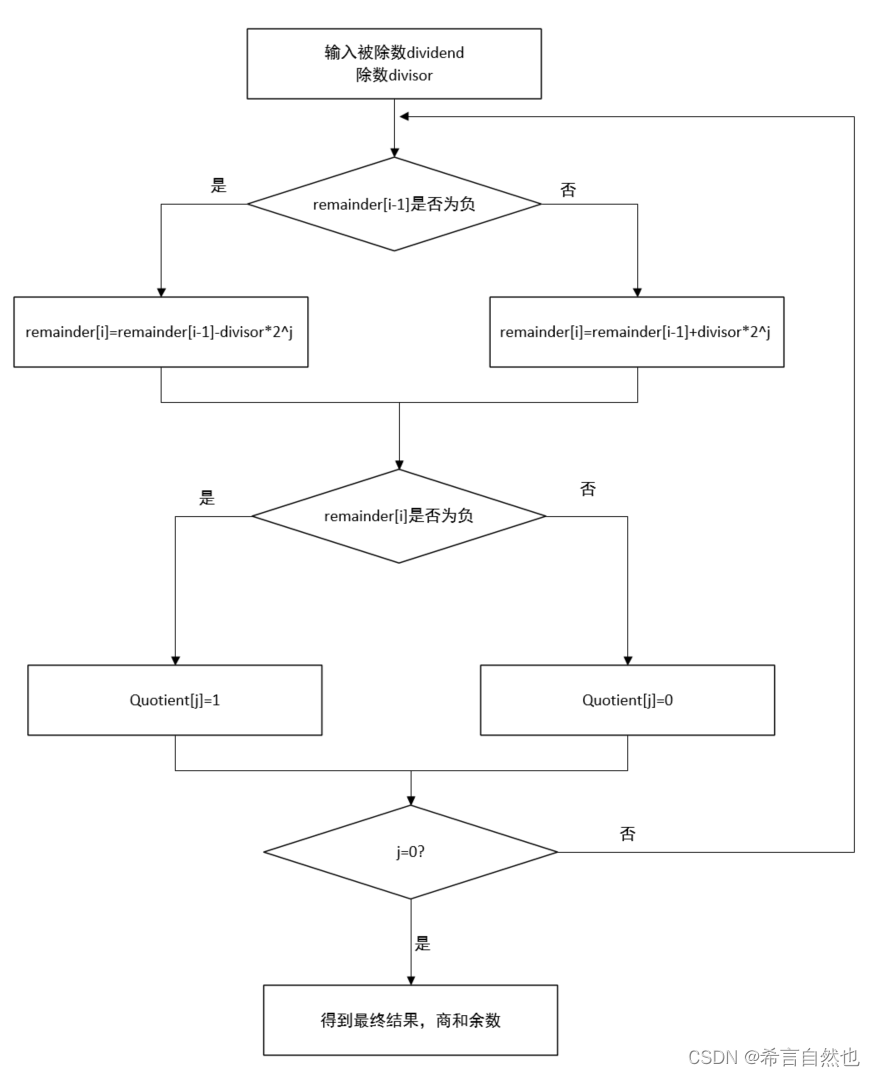
与我们直接上运算表格：

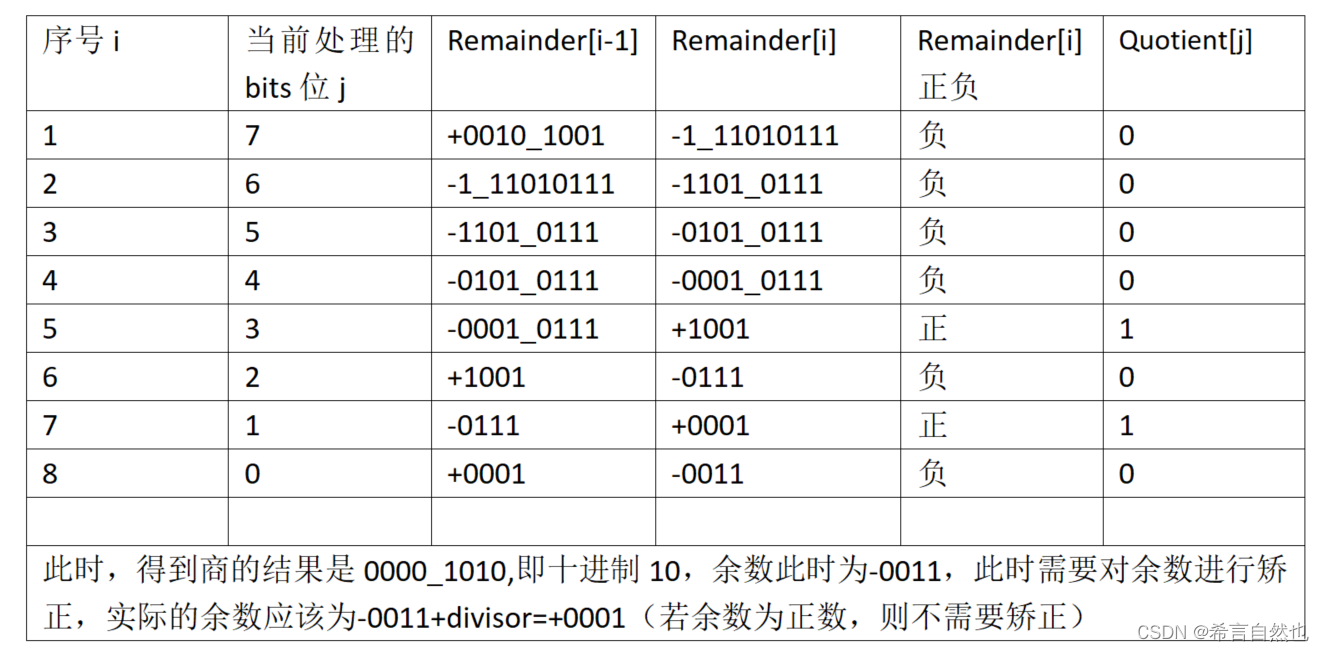
三、Vitis HLS中实现平方根解析

1、实现理论分析

一直没有找到相似的算法实现原理，但是在《算法心得-高效算法的奥秘》一书中，找到了类似的“移位并相减”的平方根算法（书中也描述了恢复余数除法和不恢复余数除法，并且计算平方根时采用了与恢复余数除法相似的办法）。书中描述复制如下（我简单分段了一下，方便观看）： “

   “9.1.1节的图9.2讲了一种硬件除法算法，与之相似，也可以用这种移位并相减的办法来计算平方根。

        在32位计算机上实现时，此算法用了一个64位寄存器，把前32位初始化为0，后面跟着待求解平方根的数据x。

        每次迭代时，64位寄存器左移两位，当前结果y(初始值为0)左移1位。

然后用64位寄存器的左半边减去2y+1。如果减法结果不是负数，那么就用其值替换掉64位寄存器的左半边，并使y=y+1(由于与以0结尾，所以将低1bits和1进行与运算即可，不需要加法器)，如果减法结果为负数，那么64位寄存器和y均保持不变。

整个过程需要16次迭代。”

根据上面信息，我们知道，“移位并相减”的平方根算法处理32bits数据时，需要16次迭代，每次迭代主要执行以下几个步骤：

（1）：x左移2bits, y左移1bits。

（2）：执行减法操作：左移后的x的高32bits，减去(2y+1)

（3）：比较第（2）步的减法结果。若为负数，则保持第（2）步的x和y不变，进行下次迭代；若为正数或者0，替换x值的高32bits为减法结果，并使y=y+1，然后进行下次迭代。

举例说明此算法：求解401的平方根（十进制401的二进制表示为：0000_0000_0000_0000_0000_0000_0000_0000___0000_0000_0000_0000_0000_0001_1001_0001）。迭代步骤如下：

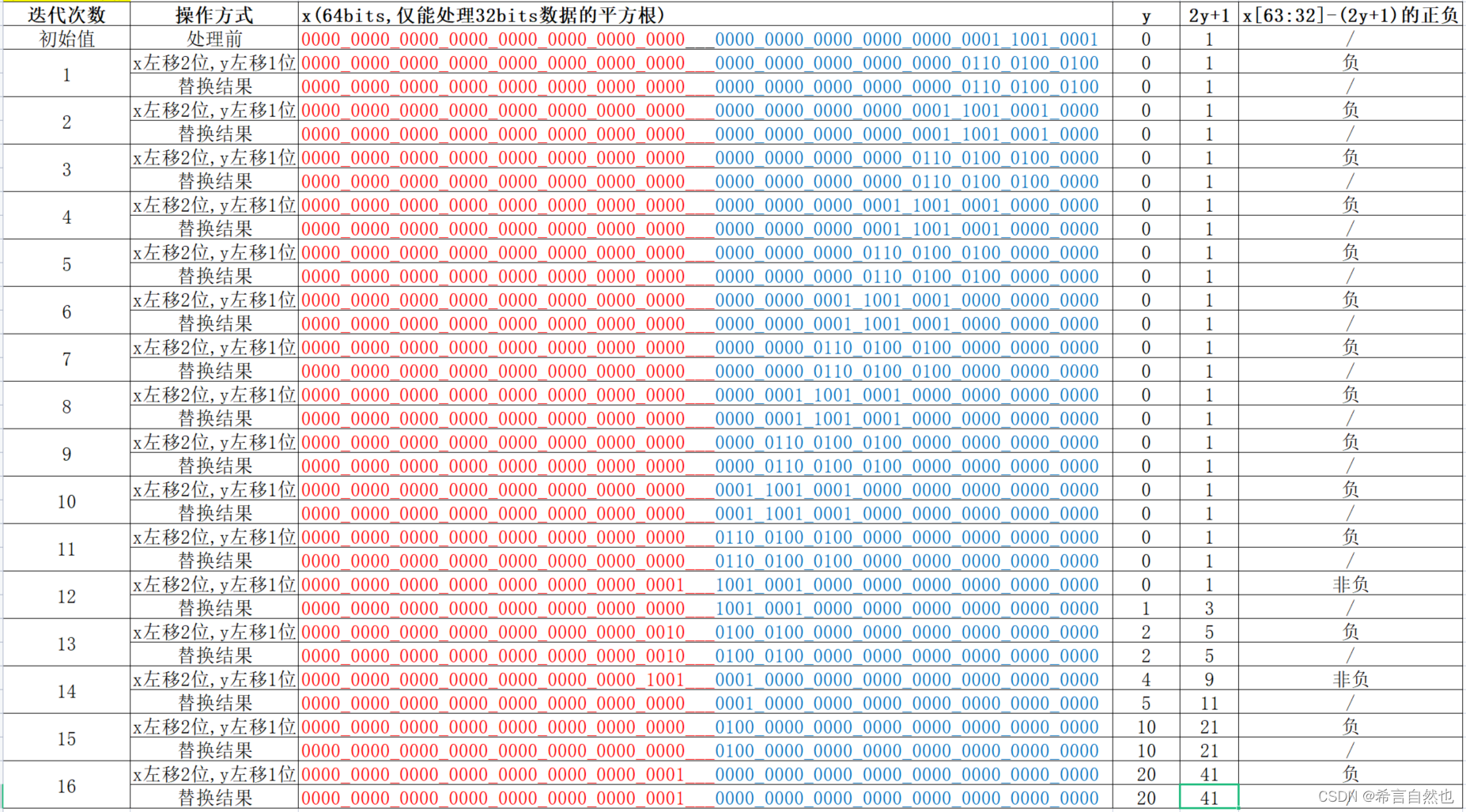
有兴趣的话，可以参考原理描述，带入到表格中一步一步迭代，看看最终结果是否正确。根据我的迭代来看，y最后取值为20，x的高32bits的结果为1，表示401的平方根为20（余数为1）。

《算法心得-高效算法的奥秘》书中给出的是类似于恢复余数除法的处理方式，但是在vitis HLS中实际上是类似于非恢复余数除法的实现形式。二者的区别就在于是否需要“恢复余数”，在vitisHLS中采用“不恢复余数”，直接修正结果的方式进行处理。这里不再具体分析，直接给出代码部分。

2、vitis HLS 库函数代码分析

/**
 * Square root computation for a 16-bit fixed point number.
 *
 * Input argument D should be 16-bit number though it is declared as 32-bit.
 * Q is the sqrt(D) and is 16-bit type
 * If format of D is QM.N (where M+N = 16) then format of Q is Q(M/2).N
 *
 *	In order to get a precision of 'n' bits in fractional part, you can simply shift left the radicand (D) by '2n'
 *	before function call and shift the solution right by 'n' to get the correct answer.
 *
 *	For example, if you want to find the square root of 35 (01100011) with one bit after decimal point i.e. N=1.
 *	You have to first find the square root of 0110001100 (shift left by 2). After you get the answer (1011) you
 *	have right shift it right by 1, so that the correct answer is 101.1 which is 5.5.
 *
 */
static int Sqrt(unsigned int D) {
    //#pragma HLS license key=IPAUVIZ_CV_BASIC
    int i;
    short int Q;
    int R;
    Q = R = 0;
    int tmp = 0;
    int tmpQ, tmpR;

    for (i = 15; i >= 0; i--) {
// clang-format off
        #pragma HLS pipeline
        // clang-format on
        if (R >= 0) {
            tmp = D >> (i + i);
            tmp = tmp & 3;
            tmpR = R << 2;
            R = tmpR | tmp;

            tmpQ = Q << 2;
            tmpQ = tmpQ | 1;

            R = R - tmpQ;
        } else {
            tmp = D >> (i + i);
            tmp = tmp & 3;
            tmpR = R << 2;
            R = tmpR | tmp;

            tmpQ = Q << 2;
            tmpQ = tmpQ | 3;

            R = R + tmpQ;
        }
        if (R >= 0) {
            Q = Q << 1;
            Q = Q | 1;
        } else {
            Q = Q << 1;
            Q = Q | 0;
        }
    }
    return Q;
}

我们可以分析此函数，获取到以下几个是重点信息：

（1）求解的是D的平方根，D为32bits的无符号整数；

（2）for循环共执行16次；

（3）Q为最终输出的平方根结果；数据位宽为16bits；

（4）其余变量：R/tmp/tmpQ/tmpR都为32bits数据；

假设要求D的平方根，在此函数中是如何处理的？首先说明一下，与非恢复余数除法相比，此函数中的参数R类似于remainder，判断R的正负，决定如何执行加减法。此函数中的参数Q类似于quotoent，为最终平方根的结果。

流程图修改如下：

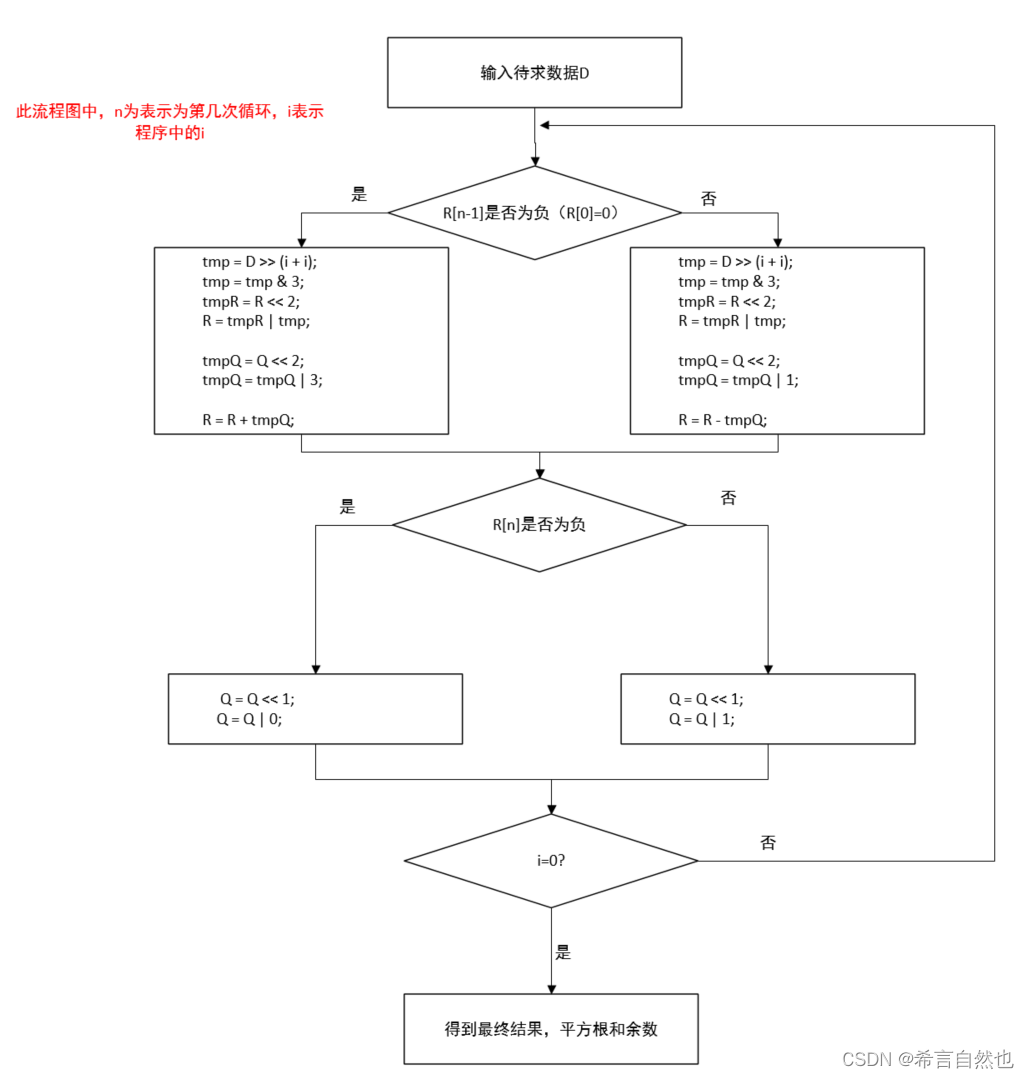
整体思想是，将上面的输入数据每次移位2bits进行与运算、或运算、相加相减的运算，由R判断是进行加还是减运算，进行最终结果的修正。基本上与除法的非恢复余数除法的流程图一样。具体可以自行演算理解。

注意：如果想要处理更高位宽数据的平方根，进需要更改循环次数，并把数据类型修改一下即可。

希言自然也

关注

21
点赞
踩
24

收藏

觉得还不错? 一键收藏
0
评论
vitis HLS中实现求平方根的库函数Sqrt解析

一直没有找到相似的算法实现原理，但是在《算法心得-高效算法的奥秘》一书中，找到了类似的“移位并相减”的平方根算法（书中也描述了恢复余数除法和不恢复余数除法，并且计算平方根时采用了与恢复余数除法相似的办法）。不恢复余数除法是对应着恢复余数除法来说的，核心是不再将数据进行恢复，而是在下一次运算时，更改remainder[i] = remainder[i-1]+D*quotient[j]*2^j的运算符号，由加法变为减法或者减法变加法，进行结果修正。此函数中的参数Q类似于quotoent，为最终平方根的结果。
复制链接

扫一扫