通俗理解贝叶斯，全概率定理

Mingsheng Zhang

已于 2022-05-08 11:38:57 修改

阅读量4.9k

点赞数 3

分类专栏：数学文章标签：概率论

于 2021-10-25 10:23:08 首次发布

本文链接：https://blog.csdn.net/youhuakongzhi/article/details/120947292

版权

数学专栏收录该内容

5 篇文章

订阅专栏

本文深入浅出地介绍了概率论中的全概率定理和贝叶斯定理。全概率定理用于计算复杂事件发生的概率，通过将事件分解为互斥的子事件并累加它们各自的成功概率。而贝叶斯定理则是在已知结果的情况下，反推导致该结果的原因的概率。通过实例解释了如何运用这两个定理解决实际问题，如计算在特定条件下事件发生的概率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

全概率定理理解：有多种方式A、B、C使你走向成功，但也可能让你失败，问你成功的概率是多少？解法为：把每一种方式成功的概率进行累加

贝叶斯定理理解：你已经成功了，现在想知道你通过方式A成功的概率是多少？

条件概率：

维基百科：（英语：conditional probability）就是事件A在事件B发生的条件下发生的概率。条件概率表示为P（A|B），读作“A在B发生的条件下发生的概率”。

定义： 设 A 与 B 为样本空间 Ω 中的两个事件，其中 P(B)>0。那么在事件 B 发生的条件下，事件 A 发生的条件概率为：

$P(A|B)={\frac {P(A\cap B)}{P(B)}}$

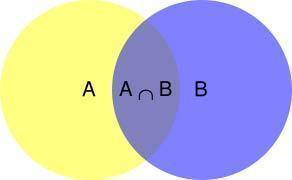
可以理解为：在B发生的条件下，A发生的概率，也可以这样来说：在B的结果中（B肯定发生），A这种情况发生的概率。从上图可以看出，B发生的条件下，A发生的概率就是图中深色的 ${\displaystyle{\frac {P(A\cap B)}{P(B)}}}$

举例来说：班级有男：12，女：10人，有带杯子的7人，其中男生：4人，女生：3人，那么问：男生中有人带杯子的概率？

这个题目解释为：在为男生的条件下（一定要是男生，这个发生的概率已经是100%），带杯子的概率是多少？即男生一共12人，其中带杯子的为4人，那么男生中有人带杯子的概率：4/12=1/3

由以上公式可以得到： $P(A\cap B) = P(A|B) P(B)$ ， $P(A\cap B) = P(B|A) P(A)$ , $P(B|A) P(A) = P(A|B) P(B)$ ，可以推出：

$P(A|B)={\frac {P(B|A)P(A))}{P(B)}}$

全概率：

维基百科：全概率定理(Law of total probability)，假设{ Bn : n = 1, 2, 3, ... } 是一个概率空间的有限或者可数无限的分割（既 Bn为一完备事件组），且每个集合Bn是一个可测集合，则对任意事件A有全概率公式：

$P(A)=\sum _{n}P(A\cap B_{n})\,$

又因为

$P(A\cap B_{n})=P(A\mid B_{n})P(B_{n}),$

此处Pr(A | B)是B发生后A的条件概率，所以全概率公式又可写作：

$P(A)=\sum _{n}P(A\mid B_{n})P(B_{n}).\,$

全概率公式将对一复杂事件A的概率求解问题转化为了在不同情况或不同原因 Bn下发生的简单事件A的概率的求和问题。即将时间A分解为不同的小的子块，计算在每一个子块发生的条件下，A发生的概率之和

以两种情况为例，如下图，假定样本空间S，是两个事件A与A'的和。计算B发生的概率，需要计算在A发生的情况下B发生的概率和A' 发生的情况下，B发生的概率。

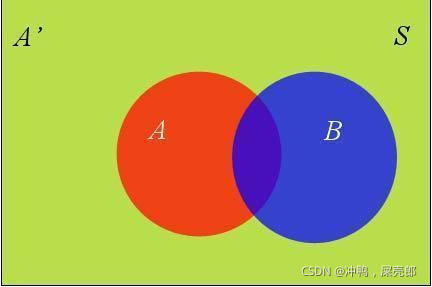
得到全概率公式：

$P(B)=P(B \cap A) + P(B \cap A') = P(B\mid A)P(A) + P(B\mid A')P(A')$

引入条件概率的公式，得到另一种条件概率的写法：

$P(A|B)={\frac {P(B|A)P(A)}{ P(B)} } = {\frac {P(B|A)P(A)}{ P(B\mid A)P(A) + P(B\mid A')P(A') }}$

贝叶斯概率

贝叶斯定理（英语：Bayes' theorem）描述在已知一些条件下，某事件的发生概率。

贝叶斯定理是关于随机事件A和B的条件概率的一则定理。

$P(A\mid B)={\frac {P(A)P(B\mid A)}{P(B)}}$

其中 $A$ 以及B为随机事件，且P(B)不为零。 $P(A\mid B)$ 是指在事件B发生的情况下事件A发生的概率。

贝叶斯定理的公式很容易从条件概率中推倒而来，

$P(B|A) P(A) = P(A|B) P(B)$

得到：

$P(A\mid B)={\frac {P(A)P(B\mid A)}{P(B)}}$

在文章最前面对贝叶斯定理的理解，已知一个结果，求解的是有A事件导致这个结果的概率是多少？相同的例子，班级有男：12，女：10人，有带杯子的7人，其中男生：4人，女生：3人，那么问：已知有个同学带了杯子，那么这个同学是女同学的概率是多少？

这个可以理解为：有个同学带了杯子，这是结果，如果把带杯子事件记为C，那么男生记为A, 女生记为B，那么拿杯子的概率为是男生并且男生拿杯子的概率+ 是女生并且女生拿杯子的概率，题目问的是已知有个同学带了杯子，那么这个同学是女同学的概率是多少？

$P(C)={P(A)P(C\mid A) + P(B)P(C\mid B) }$

由P(C)的构成可以知道，女同学拿杯子的概率占同学拿杯子的概率为：

$P(B\mid C)={\frac {P(B)P(C\mid B)}{P(C)}}} = {\frac {P(B)P(C\mid B)} {P(A)P(C\mid A) + P(B)P(C\mid B) }$

结果是：= 10/22 * 3/10 / (12/22 * 4/12 + 10/22 * 3/10) = 3/7

在贝叶斯定理中，每个名词都有约定俗成的名称：

$P(A\mid B)$ 是已知 $B$ 发生后， $A$ 的条件概率。也称作 $A$ 的后验概率。
$P(A)$ 是 $A$ 的先验概率（或边缘概率）。其不考虑任何 $B$ 方面的因素。
$P(B\mid A)$ 是已知 $A$ 发生后， $B$ 的条件概率。也可称为 $B$ 的后验概率。

参考：条件概率，全概率，贝叶斯公式理解 - 云+社区 - 腾讯云

推荐：极大似然估计详解_知行流浪-CSDN博客_极大似然估计

备注：

1. 什么是完备事件组？

设S为样本空间，B1，B2，…，Bn的一组事件。若

(i)Bi ∩ Bj=∅ （i≠j且i、j=1，2，…，n）；

(ii)B1∪B2∪…∪Bn=S，