第五章延迟计算

KuoGavin

已于 2022-08-25 09:35:48 修改

阅读量2.5k

点赞数 2

分类专栏： STA for Nanometer Designs 文章标签：静态时序分析 STA 时延计算 Elmore模型

于 2022-08-18 19:24:44 首次发布

本文链接：https://blog.csdn.net/yueguangmuyu/article/details/126134667

版权

STA for Nanometer Designs 专栏收录该内容

22 篇文章

订阅专栏

文章目录

本章主要介绍对于基于单元(cell-based)的设计布局前后时间验证中的延迟计算(delay calculation)。前面章节聚焦于互连线和单元库的建模，单元和互连线的建模技术用于获取设计的时序。

5.1 概述(Overview)

5.1.1 延迟计算基础(Delay Calculation Basics)

一个典型的设计由多种组合逻辑和时序逻辑单元组成。这里使用下图的逻辑框架来描述时延计算的概念。

单元在库中的描述指定了其输入引脚的其引脚电容值。因此，设计中的每个网络都有容性负载，该负载是该网络每个扇出的引脚负载电容加上互连线的寄生电容之和。为了简化，该部分中不考虑互连线的电容负载，在之后部分再考虑。不考虑互联寄生，上图中内部网络 $NET 0$ 的网络负载是由单元 $U A N D 1$ 和 $U NOR 2$ 输入引脚电容组成。输出引脚 $O 1$ 的负载是单元 $U NOR 2$ 加上所有输出逻辑块的电容负载。输入引脚 $I 1$ 和 $I 2$ 的引脚电容分别对应于 $U A N D 1$ 和 $U I N V 0$ 单元。基于上述抽象，上图中的逻辑设计可用下图进行等价表示。

如第三章所述，单元库包含了多种时序弧的NLDM时序模型(3.2.2 非线性时序模型(non-linear timing model))。非线性模型用输入过渡时间和输出电容的二维表格来表示。逻辑单元的输出过渡时间同样用网络的输入过渡时间和总输出负载/电容组成的二维表格来描述。因此，如果输入过渡时间(或压摆率)由逻辑块的输入指定，通过 $U I N V 0$ 和 $U A N D 1$ 单元的时序弧的输出过渡时间和延迟可以从单元库描述中得到。以此类推，可以得到通过 $U A N D 1$ 单元(从 $NET 0$ 到 $O 1$ )和通过 $U NOR 2$ 单元的其他时序弧的过渡时间和延迟。对于多输入单元(如 $U A N D 1$ )，不同的输入引脚可以提供不同的输出过渡时间值。对扇出网络过渡时间的选择取决于压摆合并(slew merge)选项，这将在5.4节中进行介绍。使用上述方法，可以基于输入引脚上的过渡时间和输出引脚上的电容来获得通过任何逻辑单元的延迟。

5.1.2 带互连线的延迟计算(Delay Calculation with Interconnect)

预布局/布局前时序

正如第四章中所述，互联寄生再预布局时序验证中使用线负载模型来进行预估。在多数情况下，线负载模型的电阻设置为 $0$ 。在这样的场景中，线负载的寄生只有电容性的，且对于设计中所有的时序弧前面部分所描述的时延计算方法同样适用。

如果线负载模型考虑了互连电阻的影响，则将 $N L D M$ 模型和总网络电容一起使用，以计算通过单元的延迟。由于互连线是电阻性的，因此从驱动单元(driver cell)的输出到扇出单元的输入引脚会有额外的延迟。互连线的延迟计算过程将在5.3节中介绍。

布局后时序

金属走线的寄生参数将被映射为驱动单元和目标单元之间的 $RC$ 网络。以图5-1中实例为例，网络的互连电阻如下图所示。内部网络(图5-1中的 $NET 0$ )映射到多个子节点，如下图。因此，反相器单元 $U I N V 0$ 的输出负载由 $RC$ 结构构成。由于 $N L D M$ 表格仅针对输入过渡时间和输出负载电容而言，因此输出引脚上的电阻性负载意味着 $N L D M$ 表格并不能直接应用。接下来介绍如何将 $N L D M$ 表格模型和互联电阻结合使用。

5.2 使用有效电容的单元延迟(Cell Delay using Effective Capacitance)

如上所述，当单元的输出负载包含互连线电阻时 $N L D M$ 模型是不能够直接使用的。因此，"有效”电容法被用来应对电阻效应。

有效电容法试图找到一个可以用作等效负载的电容，以使原始设计与具有等效电容负载的设计在单元输出的时序方面表现一致。这个等效电容被称为有效电容(effective capacitance)。

下图(a)为在扇出处有 $RC$ 互连的单元，该 $RC$ 互连可由等效的 $\pi$ 模型(4.1 互连RLC(RLC for Interconnect))表示，如下图(b)所示。有效电容的概念是为了获得等效的输出电容 $C_{eff}$ ，如下图(c)所示，此时通过单元的延迟与具有 $RC$ 互连负载的原始设计相同。通常，具有 $RC$ 互连负载的单元输出波形与具有单个电容性负载的单元输出波形非常不同。

下图展示了具有总电容，有效电容的单元的典型输出波形和和实际 $RC$ 互连的波形。选择准确的有效电容 $C_{eff}$ 应该可以使得上图(c)中单元输出处的延迟(在过渡波形的中点测得)与上图(a)中的延迟相同，如下图所示。

根据 $\pi$ 等价表示，等价电容可以表示为：

$C_{eff} = C_1 + k * C_2, \; 0 \le k \le 1$

$C_1$ 表示近端电容， $C_2$ 表示远端电容，如图5-4(b)中所示。 $k$ 的值介于 $0$ 和 $1$ 之间。在互连电阻可忽略的场景下，有效电容几乎等于总电容。这可用图5-4(b)中将 $R_{wire}$ 设置为 $0$ 来直接解释。类似的，如果互连电阻相对较大，等效电容几乎等于近端电容 $C_1$ (图5-4(b))。这可用将 $R$ 增加至限制的情况，将 $R$ 变为无穷大(本质是断路电路)。

有效电容 $C_{eff}$ 是以下各项的函数：

驱动单元(the driving cell)；
负载的特性(the characteristics of the load)，尤其是驱动单元负载的输入阻抗(input impedance)；

对于给定的互连线，一个具有驱动输出较弱的单元相对于具有驱动输出较强的单元将会有更大的等效电阻。因此，有效电容将在最小值 $C_1$ (对于高互连电阻或强驱动单元)和最大值总电容 $C_{total}=C_1+C_2$ (互联电阻可忽略或弱驱动单元)之间。注意，目标引脚的转换要晚于驱动单元的输出。近端电容充电速度比远端电容快的现象也被称为互连线的电阻屏蔽效应(resistive shielding effect)，因为驱动单元只能看到一部分远端电容。

与通过库中的 $N L D M$ 模型直接查找来计算延迟不同，延迟计算工具通过迭代过程获得有效电容。就算法而言，第一步是获取单元输出端看到的实际 $RC$ 负载的驱动点阻抗，可以使用二阶AWE或Arnoldi算法等方法计算实际 $RC$ 负载的驱动点阻抗。计算有效电容的下一步是使两种情况下直到过渡波形中点为止传输的电荷量相等：使用实际 $RC$ 负载时（基于驱动点阻抗）在单元输出处传输的电荷与使用有效电容作为负载时的电荷传输量相匹配，请注意，电荷传输匹配仅到过渡波形的中点为止。该过程从有效电容的估算值开始，然后迭代更新估算值。在大多数实际情况下，有效电容值会在少量次数的迭代中收敛。

因此，有效电容近似值是计算通过单元的延迟的优秀模型。但是，使用有效电容法获得的输出压摆（slew）与单元输出处的实际波形并不一致。有效电容近似值不能代表单元输出处的波形，尤其是波形的后半部分。请注意，在典型情况下，需要关注的波形并不是在单元输出处，而是在互连线的终点处，也即扇出单元的输入引脚处。

有多种方法可以计算互连线终点处的延迟和波形。在许多实现(implementation)方法中，有效电容的计算过程还会计算驱动单元的等效戴维宁(Thevenin)电压源。戴维宁电压源由具有串联电阻 $R_d$ 的电压源组成，如下图所示。串联电阻 $R_d$ 对应于单元输出级的下拉电阻（或上拉电阻）。

本节介绍了使用有效电容替代 $RC$ 互连来计算通过驱动单元的延迟。有效电容的计算还提供了等效的戴维宁电压源模型，然后将其用于获取通过 $RC$ 互连的时序。接下来将具体介绍获取通过 $RC$ 互连时序信息的过程。

5.3 互连延迟(Interconnect Delay)

如第四章中所述，网络的互连寄生通常使用一个 $RC$ 电路来表示。 $RC$ 互连可以是布局前也可以是布局后。对于布局后互连寄生可以包括邻接网络的耦合，基本延迟计算将所有的电容(包括耦合电容)视为接地电容。一个具有驱动单元和扇出单元的网络其寄生参数示例如下图所示。

使用有效电容法，可以分别获得通过驱动单元和通过互连线的延迟。使用有效电容法可获得通过驱动单元的延迟，并在单元的输出端提供等效的戴维宁电压源，然后使用戴维宁电压源分别计算通过互连线的延迟。互连线部分具有一个输入和与目标引脚一样多的输出。在互连线输入端使用等效戴维宁电压源，计算到每个目标引脚的延迟，如图5-6所示。

在布局前进行分析时， $RC$ 互连结构由 $RC$ 树类型决定，而RC互连结构又决定了互连线延迟。4.2节(4.2.1 互连树(Interconnect Trees))中已详细介绍了三种类型的 $RC$ 互连树表示形式，所选的RC树类型通常在库中定义。通常，最坏情况(worst-case)的慢速库会选择最坏情况的 $RC$ 树，因为该类型的树提供了最大的互连线延迟。类似地，最佳情况(best-case)的 $RC$ 树结构中不包括从源引脚到目标引脚的任何电阻，通常在最佳情况的快速工艺角时被选择。因此，最佳情况 $RC$ 树的互连延迟等于零。典型(typical)情况 $RC$ 树和最坏情况 $RC$ 树的互连延迟的处理方式与布局后 $RC$ 互连一样。

Elomore延迟模型

Elmore延迟模型(如图5-8所示)适用于 $RC$ 树。什么是 $RC$ 树？ $RC$ 树应满足以下三个条件：

有单一的输入(源)节点；
没有任何电阻回路；
所有电容都在节点和地之间；

Elmore延迟可以看作是找到每段的延迟，即 $R$ 与下游电容的乘积，然后取各延迟之和。

对于大量的中间节点其时延表示为：

$\begin{align*} & T_{d1}=C_1*R1;\\ & T_{d2}=C_1*R1+C_2*(R_1+R_2); \\ & ... \\ & T_{dn}=\sum_{i=1,...,N}C_i(\sum_{j=1,...,i}R_j); \;\; \#Elmore \; delay \; equation \end{align*}$

Elmore延迟在数学上考虑的是脉冲响应的第一时刻。现在，我们将Elmore延迟模型进行如下简化表示：互连线的寄生电阻与电容分别为 $R_{wire}$ 和 $C_{wire}$ ，互连线远端的引脚电容由负载电容 $C_{load}$ 来建模。等效的 $RC$ 网络可以简化为 $\pi$ 模型或 $T$ 模型，分别如前面章节四中图4-4和图4-3所示。两种模型都具有如下走线延迟(基于Elmore延迟方程)：

$R_{wire}*(C_{wire}/2 + C_{load})$

这是因为 $C_{load}$ 在充电路径中能看到整个互连线的电阻，而 $C_{wire}$ 电容在T模型中仅能看到 $R_{wire}/2$ 且 $C_{wire}/2$ 在 $\pi$ 模型中能看到 $R_{wire}$ 。以上方法也可以扩展到更复杂的互连结构。

下面给出了使用线负载模型和平衡(balanced) $RC$ 树(以及最坏情况RC树)计算一个网络的Elmore延迟的示例。

使用平衡 $RC$ 树模型时，网络的电阻和电容在网络的各个分支之间平均分配（假设扇出为 $N$ ）。对于具有引脚负载 $C_{pin}$ 的分支，使用平衡 $RC$ 树的延迟为：

$Net \; delay = (R_{wire}/N)*(C_{wire}/(2*N)+C_{pin})$

使用最坏情况RC树模型时，网络的每个分支终点都考虑了网络的电阻和整个电容。此时的延迟值如下所示，这里的 $C_{pins}$ 是所有扇出的总引脚负载：

$Net \; delay = R_{wire} * (C_{wire} / 2 + C_{pins})$

图5-9展示了示例设计。

如果我们使用worst-case树模型来计算网络 $N 1$ 的延迟，我们得到：
$Net \; delay = R_{wire}*(C_{wire}/2 + C_{pins}) = 0.3*(0.5+2.3)=0.84$

如果使用平衡树模型，我们得到网络 $N 1$ 的两分支的延迟如下：
$Net\; delay\; to\; NOR2\; input\; pin=(0.3/2)*(0.5/2+1.3)=0.2325 \\ Net\; delay\; to\; BUF\; input\; pin=(0.3/2)*(0.5/2+1.0)=0.1875$

高阶互连线延迟估计(High order Interconnect Delay Estimation)

如上所述，Elmore延迟考虑的是脉冲响应的第一时刻，而AWE(渐近波形评估)、Arnoldi或其他方法能够匹配更高阶的响应时刻。通过进行更高阶的估计，可以提高计算互连线延迟的精度。

全部片上延迟计算(Full Chip Delay Calculation)

到目前为止，本章已经介绍了单元延迟以及单元输出处互连线的延迟计算。因此，给定在单元输入处的过渡时间，可以计算通过单元和单元输出处互连线的延迟。互连线远端(终点)的过渡时间是下一级的输入，整个设计过程中都会重复此过程，这样就计算出了设计中每个时序弧的延迟。

5.4 压摆合并(Slew Merging)

当多个压摆到达一个公共点时(例如在多输入单元的情况下)会发生什么呢？这种公共点称为压摆合并点(slew merge point)。选择哪个压摆在压摆合并点处继续向下传播呢？考虑图5-10所示的两输入单元。

由于引脚 $A$ 上的信号改变，引脚 $Z$ 上的压摆到达较早，但上升缓慢(压摆较小)；由于引脚 $B$ 上的信号改变，引脚 $Z$ 上的压摆到达较晚，但上升很快(压摆较大)。在压摆合并点(例如引脚 $Z$ )，应选择哪个压摆进一步传播呢？取决于所执行的时序分析的类型(最大或最小时序路径分析)，这些压摆值中的任何一个都可能是正确的。

进行最大时序路径分析时有两种可能性：

最差的压摆传播(Worst slew propagation)：此模式选择要在合并点传播最坏的压摆，这将是图5-10(a)中的压摆。对于通过引脚 $\rarr Z$ 的时序路径，此选择是准确的，但对于通过引脚 $B\rarr Z$ 的任何时序路径都是悲观的。
最差的到达时间传播(Worst arrival propagation)：此模式选择要在合并点传播最差的到达时间，这对应于图5-10(b)中的压摆。在这种情况下选择的压摆对于通过引脚 $B\rarr Z$ 的时序路径是准确的，但对于通过引脚 $A\rarr Z$ 的时序路径是乐观的。

类似进行最小时序路径分析时也有两种可能性：

最佳的压摆传播(Best slew propagation)：此模式选择要在合并点传播最佳的压摆，这就是图5-10(b)中的压摆。对于通过引脚 $B\rarr Z$ 的时序路径，此选择是准确的，但对于通过引脚 $A\rarr Z$ 的任何时序路径，该选择的压摆值较小。对于经过 $A\rarr Z$ 的路径，路径延迟小于实际值，因此对于最小时序路径分析是悲观的。
最佳的到达时间(Best arrival propagation)：此模式选择要在合并点传播最佳的到达时间，这对应于图5-10(a)中的压摆。在这种情况下，选择的压摆对于通过引脚 $A\rarr Z$ 的时序路径是准确的，但大于通过引脚 $B\rarr Z$ 的时序路径的实际值。对于经过 $B\rarr Z$ 的路径，路径延迟大于实际值，因此对于最小时序路径分析是乐观的。

设计人员可以在静态时序分析环境之外执行延迟计算，以生成SDF(Standard Delay Format)文件。在这种情况下，延迟计算工具通常使用最差的压摆传播。生成的SDF文件足以用于最大时序路径分析，但对于最小时序路径分析可能是过于乐观的。

大多数静态时序分析工具均使用最差和最佳的压摆传播作为默认设置，因为它会保守地限制分析。但是，在分析特定路径时可以使用精确的压摆传播，精确的压摆传播需要在时序分析工具中启用一个选项。因此，重要的是要了解静态时序分析工具中默认使用哪种压摆传播模式，并清楚其可能过于悲观的情况。

5.5 不同压摆阈值(Different Slew Thresholds)

一般而言，一个库会指定在单元表征(characterization)期间使用的压摆(过渡时间)阈值。问题是，当具有一组压摆阈值的单元驱动其他具有不同压摆阈值设置的单元时，会发生什么呢？考虑图5-11中所示的情况，具有 $20\%-80\%$ 压摆阈值的单元驱动两个扇出单元，其中一个具有 $10\%-90\%$ 的压摆阈值，另一个具有 $30\%-70\%$ 的压摆阈值且压摆降额系数为 $0.5$ 。

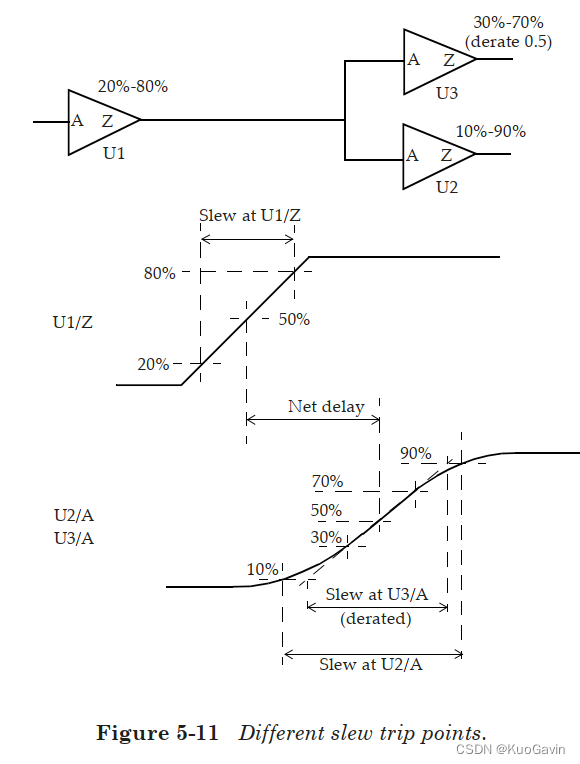
单元 $U 1$ 在单元库中的压摆设置定义如下：

slew_lower_threshold_pct_rise : 20.00
slew_upper_threshold_pct_rise : 80.00

slew_derate_from_library : 1.00
input_threshold_pct_fall : 50.00
output_threshold_pct_fall : 50.00
input_threshold_pct_rise : 50.00
output_threshold_pct_rise : 50.00
slew_lower_threshold_pct_fall : 20.00
slew_upper_threshold_pct_fall : 80.00

$U 2$ 单元的压摆设置在另一个单元库中定义如下：

slew_lower_threshold_pct_rise：10.00
slew_upper_threshold_pct_rise：90.00

slew_derate_from_library：1.00
slew_lower_threshold_pct_fall：10.00
slew_upper_threshold_pct_fall：90.00

$U 3$ 单元的压摆设置在另一个单元库中定义如下：

slew_lower_threshold_pct_rise : 30.00
slew_upper_threshold_pct_rise : 70.00

slew_derate_from_library : 0.5
slew_lower_threshold_pct_fall : 30.00
slew_upper_threshold_pct_fall : 70.00

上述只展示了 $U 2$ 和 $U 3$ 的压摆相关设置；输入和输出时延相关的阈值设置为 $50\%$ 且并未展示。时延计算工具计算过渡时间根据连接到这个网络的单元的压摆阈值。

延迟计算工具会根据 $U 2/ A$ 和 $U 3/ A 处$ 的波形及其压摆阈值，计算出 $U 2/ A$ 和 $U 3/ A$ 处的压摆。请注意， $U 2/ A$ 的压摆是基于 $10\%-90\%$ 设置的，而 $U 3/ A$ 所用的压摆是基于 $30\%-70\%$ 设置，然后根据库中指定的压摆降额(slew derate)系数(3.2.3 阈值规格和压摆降额) $0.5$ 使用的。此示例说明了如何根据切换波形和扇出单元的压摆阈值设置来计算扇出单元输入端的压摆。

在可能不考虑互连电阻的预布局(pre-layout)设计阶段时，可以按以下方式计算具有不同阈值的网络处的压摆。例如， $10\%-90\%$ 压摆阈值和 $20\%-80\%$ 压摆阈值之间的关系为：

$slew_{20-80} / （0.8 - 0.2） = slew_{10-90} / （0.9 - 0.1）$

因此， $10\%-90\%$ 阈值测量点设置时的 $500 p s$ 压摆对应于 $20\%-80\%$ 阈值测量点设置时 $(500 p s * 0.6) /0.8 = 375 p s$ 的压摆。类似地， $20\%-80\%$ 阈值测量点设置时的 $600 p s$ 压摆对应于 $10\%-90\%$ 阈值测量点设置时 $(600 p s * 0.8) /0.6 = 800 p s$ 的压摆。

5.6 不同电压域(Different Voltage Domains)

一个典型设计可能会使用不同的电源供应对于芯片的不同部分。在这些案例中，电平转换单元(level shifting cell)用于不同电压域间的接口处。电平转换单元在一个电压域接受输入，而在另一个电压域提供输出。例如，一个标准单元可以为 $1.2 V$ ，其输出可以为较低电压，如 $0.9 V$ 。下图即为一个示例，其中延迟是根据 $50\%$ 阈值点计算的。对于接口单元的不同引脚，这些引脚可能处于不同的电压：

5.7 路径延迟计算(Path Delay Calculation)

一旦得到了每个时序弧的全部延迟，则可以将设计中各个单元的时序表示为时序图。通过组合逻辑单元的时序可以表示为从输入到输出的时序弧。类似地，互连线可用从源引脚到每个目的引脚(destination / sink)的相应弧表示，表示为单独的时序弧。一旦整个设计由相应的时序弧标定(annotate)了，计算路径延迟就是将沿路径的所有网络和单元的时序弧相加起来即可。

5.7.1 组合逻辑路径延迟(Combinational Path Delay)

考虑图5-13中的串联的三个反相器的情况。当考虑从网络 $N 0$ 到 $N 3$ 的路径，同时考虑上升沿和下降沿路径。假定此时网络 $N 0$ 有一个上升沿。

第一个反相器的输入过渡时间可能已经指明；在该设定不存在时，设定过渡时间为0(相当于理想情况)。反相器 $U I N Va$ 的输入过渡时间用上节中所指定的互连时延模型来决定。相同的时延模型也被用来决定时延 $T n 0$ ，也即网络 $N 0$ 的时延。

根据 $U I N Va$ 输出处的 $RC$ 负载，可以获得输出处 $U I N Va / Z$ 的有效电容。输入处 $U I N Va / A$ 的过渡时间和输出处 $U I N Va / Z$ 的等效有效负载则可用于获得单元输出下降延迟(output fall delay)。

等效的戴维宁电压源模型在引脚 $U I N Va / Z$ 上通过互连延迟模型可确定引脚 $U I N Vb / A$ 上的过渡时间，互连延迟模型还用于确定网络 $N 1$ 上的延迟 $T n 1$ 。

一旦知道了输入 $U I N Vb / A$ 的过渡时间，就可以类似地计算通过 $U I N Vb$ 的延迟。 $U I N Vb / Z$ 处的 $RC$ 互连以及引脚 $U I N V c / A$ 的引脚电容可用于确定 $N 2$ 处的有效负载。 $U I N Vb / A$ 处的过渡时间可用于确定通过反相器 $U I N Vb$ 的输出上升延迟(output rise delay)，依此类推。

最后一级的负载由明确的负载说明来指定，如果没有指定，则仅使用网络 $N 3$ 的线负载。

上述分析假设网络 $N 0$ 为上升沿，对于网络 $N 0$ 的下降沿，可以进行类似的分析。因此，在这个简单的示例中，存在两条具有以下延迟的时序路径：

$\begin{align*} T_{fall} = Tn0_{rise} + Ta_{fall} + Tn1_{fall} + Tb_{rise} + Tn2_{rise} + Tc_{fall} + Tn3_{fall} \\ T_{rise} = Tn0_{fall} + Ta_{rise} + Tn1_{rise} + Tb_{fall} + Tn2_{fall} + Tc_{rise} + Tn3_{rise} \end{align*}$

通常，由于驱动单元输出处的戴维宁电压源模型不同，通过互连线的上升和下降延迟可能会有所不同。

5.7.2 寄存器路径(Path to a Flip-flop)

寄存器路径输入

考虑如下图所示从输入 $S D T$ 到寄存器 $U FF 1$ 路径的时序。

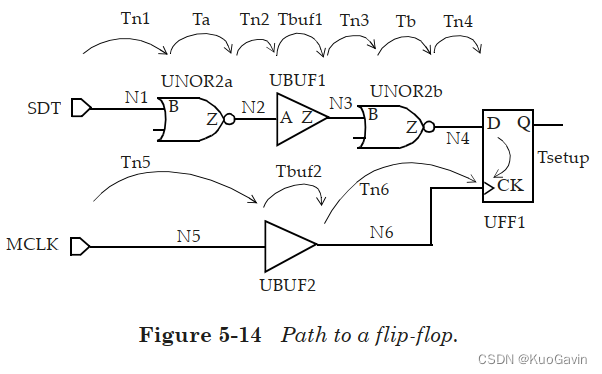
我们需要同时考虑上升沿和下降沿路径。对于上升沿情况下的输入 $S D T$ ，数据路径的时延是：

$Tn1_{rise} + Ta_{fall} + Tn2_{fall} + Tbuf1_{fall} + Tn3_{fall} + Tb_{rise} + Tn4_{rise}$

类似的，对于下降沿情况下的输入 $S D T$ ，数据路径的时延是：

$Tn1_{fall} + Ta_{rise} + Tn2_{rise} + Tbuf1_{rise} + Tn3_{rise} + Tb_{fall} + Tn4_{fall}$

输入 $MC L K$ 上升沿的捕获(capture)时钟路径延迟为：

$Tn5_{rise} + Tbuf2_{rise} + Tn6_{rise}$

触发器到触发器路径

图5-15给出了两个触发器之间的数据路径和相应的时钟路径的示例：

$U FF 0/ Q$ 上升沿的数据路径延迟为：

$Tck2q_{rise} + Tn1_{rise} + Ta_{fall} + Tn2_{fall} + Tb_{fall} + Tn3_{fall}$

输入 $PC L K$ 上升沿的发起(launch)时钟路径延迟为：

$Tn4_{rise} + T5_{rise} + Tn5_{arise}$

输入 $PC L K$ 上升沿的捕获(capture)时钟路径延迟为：

$Tn4_{rise} + T5_{rise} + Tn5b_{rise} + T6_{rise} + Tn6_{rise}$

需要注意单元的单边性(unateness)，因为边沿方向在通过单元时可能会改变(上升沿变下降沿，下降沿变上升沿)。

5.7.3 多路径(Multiple Paths)

在任何两点之间，可以有很多路径。最长的路径是花费时间最多的路径，这也称为最差路径、较晚路径或最大路径。最短的路径是花费时间最少的路径，这也称为最佳路径、较早路径或最小路径。(2.8 最小与最大时序路径(min and max timing paths))

请参见图5-16中时序弧的逻辑和延迟。两个触发器之间的最长路径是通过单元 $U B U F 1$ 、 $U NOR 2$ 和 $U N A N D 3$ ，两个触发器之间的最短路径是通过单元 $U N A N D 3$ 。

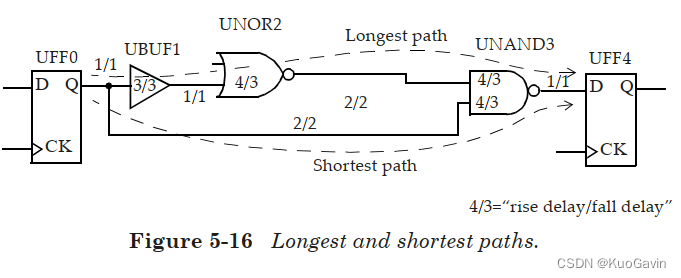
5.8 裕量计算(Slack Calculation)

裕量(Slack)是信号需要到达时间(Required Time)与实际到达时间(Arrival Time)之差。在图5-17中，要求数据在 $7 n s$ 时保持稳定才能满足建立时间(setup)要求。但是，数据在 $1 n s$ 时就已稳定。因此，裕量为 $6 n s (= 7 n s - 1 n s)$ 。