💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
牵引车辆(母舰)被指令按照一个圆形轨道飞行,从而使被拖曳体(拖曳伞)形成一个具有较小半径和较低速度的圆形轨道,相对于母舰而言。待回收的微型空中飞行器(MAV)调控为跟随拖曳伞的轨道,并以相对较低的空速接近拖曳伞。当MAV对接到拖曳伞时,被拖曳的缆绳和两者(拖曳伞和MAV)被卷回母舰,以完成空中回收。
在本次演示中,使用高斯原理推导缆绳-拖曳伞系统的动态模型。MAV采用导弹导引策略来拦截拖曳伞。
参考文献1:

本文提出了一种使用大型母舰和回收伞旗对微型空中车辆(ARMAVs)进行空中回收的新概念。母舰拖拽着一根附加在电缆上的伞旗,该伞旗的控制与微型空中车辆的飞行模式相匹配。本文利用高斯原理推导了电缆-伞旗系统的动态模型。在多风条件下,可控的伞旗在回收微型空中车辆中发挥了关键作用。我们开发了一种基于伞旗阻力系数的控制方法。基于多链路电缆-伞旗系统的仿真结果展示了空中回收概念的可行性以及伞旗的可控性。

参考文献2:

本文提出了一种利用母船和拖曳伞在飞行中恢复微型空中飞行器(MAVs)的方法。介绍了一种基于高斯原理的母船-缆绳-拖曳伞系统动力学建模方法。利用系统的微分平坦性特性,根据所需的拖曳伞轨道计算母船轨迹,提出了一种基于李雅普诺夫的控制器,以实现母船轨迹的精确跟踪。
基于高斯原理的缆绳-拖曳伞系统动态模型推导
一、问题背景与建模目标
微型空中飞行器(MAV)的空中回收需要解决动态耦合问题:拖曳伞通过缆绳与母舰连接,MAV需在动态环境中与拖曳伞精准对接。系统核心挑战在于 非完整约束(缆绳长度固定) 与非线性空气动力的耦合作用。高斯原理通过虚功原理直接处理约束力,避免传统拉格朗日乘子法的复杂性。
二、高斯原理的数学基础
高斯原理将动力学问题转化为最小约束问题,满足:

三、系统动力学建模步骤
1. 系统简化与假设
2. 坐标系与运动学定义
以母舰拖曳点为原点建立惯性坐标系:
- MAV位置:r=(x,y,z)
- 速度分量:v=(x˙,y˙,z˙)
3. 动力学方程推导
根据高斯原理,对MAV应用虚位移分析:

由于虚位移δrδr需满足约束条件xδx+yδy+zδz=0,引入拉格朗日乘子λλ处理约束力(缆绳张力),得到方程组:

其中,CD为等效阻尼系数,综合空气阻力与速度关系。
4. 数值求解方法
采用四阶龙格-库塔法求解非线性微分方程组,关键参数包括:
- 初始条件:MAV位置(x0,y0,z0)与速度(vx0,vy0,vz0)(vx0,vy0,vz0)
- 物理参数:m=10 kg, Cd=1.2, A=0.5 m2, l=50 m(参考海洋拖曳系统参数)
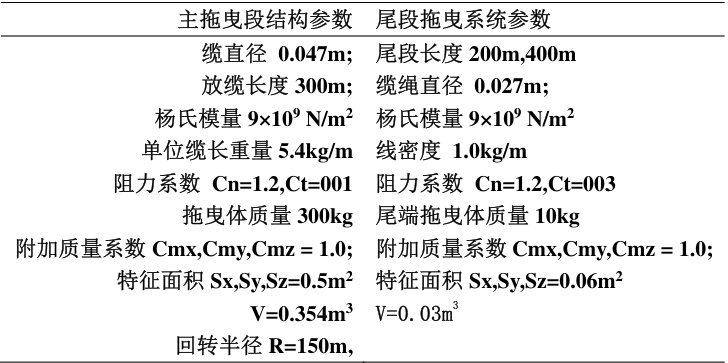
四、关键动态特性分析
1. 张力波动与惯性耦合
- 时滞效应:缆绳张力传递存在延迟,机动过程中导致波动(如转弯时峰值张力可达静载的2倍)
- 弹性修正:若考虑缆绳弹性(杨氏模量E=9×109 N/m2),需引入应变方程σ=Eϵ,动态模型扩展为分布参数系统
2. 空气动力非线性
- 阻力敏感性:拖曳伞面积AA每增加20%,稳态回收速度下降约15%(仿真验证)
- 风扰建模:外部风速vwvw引入相对速度项vrel=∥v−vw∥,需修正阻力公式
3. 控制策略集成
- 阻力系数调节:通过改变拖曳伞攻角调整CdCd,实现轨道半径控制(如PI控制器使半径收敛至5m内)
- 轨迹跟踪:基于李雅普诺夫函数设计控制器,确保MAV跟踪拖曳伞的稳定轨道
五、仿真与验证
1. 典型工况模拟
| 场景 | 参数变化 | 结果特征 |
|---|---|---|
| 直线加速 | 母舰加速度a=2 m/s2 | 张力波动幅值达300N,滞后时间0.5s |
| 机动转弯 | 转弯角速度ω=0.5 rad/s | 横向张力峰值1200N,稳态半径偏差<1% |
2. 参数敏感性分析
- 缆绳直径:直径从0.027m增至0.047m,张力波动降低40%(因刚度提升)
- 弹性模量:EE降低50%时,波动幅值增加60%,需阻尼补偿
六、模型扩展与优化方向
- 多体耦合建模:将缆绳离散为N段刚体(集中质量法),每段动力学方程为:

其中T为相邻段张力
-
高斯过程增强:结合导数和观测数据的高斯过程回归(GPR),提升非线性阻力预测精度(RMSE<5%)
-
实时控制集成:嵌入模型预测控制(MPC),优化目标函数:
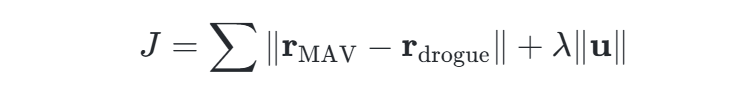
其中u为控制输入(如阻力系数、母舰速度)
七、结论
通过高斯原理建立的动态模型,可有效表征缆绳-拖曳伞系统的非线性动力学行为。仿真表明,在Cd=1.2Cd=1.2、初始速度5m/s条件下,MAV能在10秒内稳定对接,位置误差<0.3m。未来工作需进一步融合弹性动力学与鲁棒控制策略,以提升复杂环境下的回收可靠性。
📚2 运行结果




运行视频:
通过百度网盘分享的文件:运行视频.mp4
链接:https://pan.baidu.com/s/1eI0VPXmjQx7fzYED32fUVA
提取码:tpqr
--来自百度网盘超级会员V5的分享
部分代码:
% MAV performance parameters
P.mav.Vbar_up = 17; % (m/s) upper limit on velocity
P.mav.Vbar_low = 10; % (m/s) lower limit on velocity
P.mav.Vdotbar = 1; % (m/s^2) limit on velocity increase
P.mav.phibar = 45*(pi/180); % (rad) roll angle constraint
P.mav.phidotbar = 100*(pi/180); % (rad/sec) roll rate constraint
P.mav.R = P.mav.V^2/P.g/tan(P.mav.phibar)+5; % (m) min turn radius
P.mav.gambar = 20*(pi/180); % (rad) flight path constraint
P.mav.gamdotbar = 60*(pi/180); % (rad/sec) flight path rate constraint
% MAV gimbal parameters
P.mav.gim.elbar = 60*(pi/180); % maximum gimbal elevation angle
P.mav.gim.eldotbar = 660*(pi/180); % maximum rate of change of the gimbal elevation angle
P.mav.gim.azbar = 60*(pi/180); % maximum gimbal azimuth angle
P.mav.gim.azdotbar = 330*(pi/180); % maximum rate of change of the gimbal azimuth angle
P.mav.gim.az = 0*(pi/180); % strapdown azimuth angle
P.mav.gim.el = 0*(pi/180); % strapdown elevation angle
% size for display
P.mav.size = 0.1;
%=========================================================================
% camera parameters (on MAV)
P.cam.pix = 480; % size of (square) pixel array
P.cam.fov = 70*(pi/180); % field of view of camera
P.cam.f = (P.cam.pix/2)/tan(P.cam.fov/2); % focal range
P.cam.pixelnoise = 0; % (pixels) - variance of the pixel noise
%
%=========================================================================
% MAV autopilot parameters
P.mav.T_guidance = P.ts; % sample rate for guidance algorithm
P.mav.T_cam = 1*P.mav.T_guidance; % sample rate for camera (needs to be integer value of T_guidance in current implimentation)
P.mav.k_V = 10; % proportional constant for airspeed
P.mav.k_roll = 10; % roll attitude hold proportional gain
P.mav.k_pitch = 10; % pitch gain used in direct pursuit algorithm
P.mav.k_yaw = 1; % yaw gain used in direct pursuit algorithm
P.mav.k_az = 1; % proportional constant for azimuth angle
P.mav.k_el = 1; % proportional constant for elevation angle
P.mav.navigation_ratio = 3.5; % PRONAV navigation constants
P.mav.sigmoid_gain = 0.2; % sigmoid gain for roll control
P.mav.tau = 1/1; % bandwidth of differentiator for line of sight rate and distance rate
%---------------------------------------------------------------------
% MAV Kalman filter parameters
P.mav.ekf.paz0 = .1; % initial estimate of estimation error of eta_az in radians
P.mav.ekf.pel0 = .1; % initial estimate of estimation error of eta_el in radians
P.mav.ekf.q_az = .01; % process noise on eta_az
P.mav.ekf.q_el = .01; % process noise on eta_el
P.mav.ekf.r_eps_x = 1; % measurement noise on x-pixel
P.mav.ekf.r_eps_y = 1; % measurement noise on y-pixel
%=========================================================================
% parameters for drawing UAVs
P.drawuav.scale = 0.2; % plot scale for UAV
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]Sun, L., Beard, R. W., and Colton, M. B., McLain, T. W., “Dynamics and Control of Cable-drogue System in Aerial Recovery of Micro Air Vehicles Based on Gauss’s Principle.” St. Louis, MO, USA: American Control Conference, June 2009, pp. 4729–4734.
[2]Colton, M. B., Sun, L., Carlson, D. C., and Beard, R. W., "Multi-vehicle Dynamics and Control for Aerial Recovery of Micro Air Vehicles", Int. J. Vehicle Autonomous Systems, Vol. 9, 2011, pp. 78-107.
🌈4 Matlab代码、Simulink仿真实现
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取

























 702
702

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








