(补充:
(1)数学期望-----即所有样本的均值
(2)方差------------即样本与均值的差的平方的和
(3)标准差---------即对方差开2次根号)
0-1分布(伯努利分布、两点分布)-----离散概率分布
若随机变量X只取两个可能值0,1 ,且
- P{X = 1} = p,P{X = 0} = q
其中0<p<1,q = 1 - p,则称X服从0-1分布
伯努利分布的数学期望与方差
二项分布-----其本质就是n重伯努利实验-----离散概率分布
若随机变量X可能取值0,1,2...,n,且X分布规律为
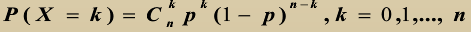
其中0<p<1, p+q = 1, 则称X服从参数为 n,p的二项分布。
二项分布的数学期望与方差
泊松分布(用以描述 “单位时间或单位空间内,某一事件发生的次数” 这样的问题)-----离散概率分布
若随机变量X的可能取值0,1,2,...,n,X的分布规律为
其中,则称X服从参数为
的泊松分布。记为

二项分布与泊松分布的关系
泊松分布的数学期望与方差
(补充:概率密度
如果对于随机变量X的分布函数F(X),存在非负函数f(x),使得对于任意实数x,有
则称X为连续性随机变量,其中函数f(x)称为X的概率密度函数。
在数学中,连续型随机变量的概率密度函数是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。
概率密度函数并没有实质的意义,只是对于连续性随机变量,我们关心他在某一点取值的问题没有太大的意义,而是关心它在某一区间上取值的问题,故引入了概率密度函数。)
正态分布(高斯分布---Gauss)----连续概率分布
若随机变量X的概率密度函数为
,则称X服从


正态密度函数图形的性质:
(1)曲线关于直线对称,这表明:对于任意的h>0,有
(2)当时,f(x)取到最大值
,x离
越远,f(x)的值就越小,这表明,对于同样长度的区间,当区间离
越远时,随机变量X落在该区间中的概率就越小。
(3)曲线y = f(x)在处有拐点;曲线y = f(x)以OX轴为渐进线。
(4)若
的值,则发f(x)的图形沿x轴平行移动,但不改变其形状。因此y = f(x)图形的位置完全由参数

(5)若
的值,由于f(x)的最大值为

越小时,y = f(x)的图形越陡,因而X落在


标准正态分布

 。其密度函数表示为:
。其密度函数表示为:




均匀分布





指数分布
 ,则称X服从参数为
,则称X服从参数为 的指数分布,记作
的指数分布,记作 ,
,












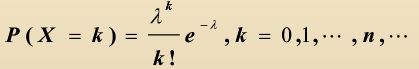




























 2560
2560

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








