概率论




线性代数
第一章n阶行列式与克莱默法则:用n阶行列式求解n元方程组。
第二/三章矩阵与线性方程组。矩阵的秩与方程组的解。
第四章向量组的线性相关性。向量空间、超平面。
第五章相似矩阵和二次型。内积、范数、正交。
第六章线性空间:向量空间的概念是集合与运算二者的结合,一般的说,同一个集合,若定义两种不同的线性运算,就构成不同的向量空间;若定义的运算不是线性运算,就不能构成向量空间。所以,所定义的线性运算是向量空间的本质,而其中的元素是什么倒并不重要。由此可以说把向量空间叫做线性空间更为合适。
统计学

数值分析

第一章 引言
数值分析是研究数值问题的算法,概括起来有四点:
- 面向计算机,算法只能包括加、减、乘、除运算和逻辑运算
- 有可靠的理论分析,能任意逼近并达到精度要求,对近似算法要保证收敛性和数值稳定性,还要对误差进行分析
- 要有好的计算复杂性,时间复杂性好是指节省计算时间,空间复杂性好是指节省存储空间
- 要有数值实验,即任何一个算法除了从理论上要满足上述三点外,还要通过数值试验证明
一个算法如果输入数据有误差,而在计算过程中舍入误差不增长,则称此算法是数值稳定的。
如果输入数据有微小扰动(即误差),引起输出数据(即问题解)相对误差很大,这就是病态问题。
第二章 插值
在函数f(x)两个点之间插入多个点,插入要求是既能反映函数f(x)的特性,又便于计算的简单函数。即插值函数P(x)。应用举例:用计算机程序控制加工机械零件,控制每步走刀。P(x)举例:
- 最简单的多项式插值
- 其次拉格朗日插值。但节点增减时,计算要全部重新进行
- 为了计算方便设计一种逐次生成插值多项式的方法,牛顿均差插值
- 插值多项式在插值节点上函数值相等,有的实际问题还要求在节点上导数值相等甚至高阶导数值也相等,即埃尔米特插值多项式
- 一般总认为插值函数的次数越高,逼近f(x)的精度越好,但实际上并非如此,这是因为对任意的插值节点,当n→∞时,Ln(x)不一定收敛于f(x)。因而不用高次插值,而用分段低次插值
- 分段低次插值函数都有一致收敛性,但光滑性较差,对于像高速飞机的机翼形线、船体放样等型值线往往要求有二阶光滑度,即有二阶连续导数。早期工程师制图时,把富有弹性的细长木条(所谓样条)用压铁固定在样点上,在其他地方让它自由弯曲,然后延木条画下曲线称为样条曲线。样条曲线实际上是由分段三次曲线并接而成,在连接点即样点上要求二阶导数连续,从数学上加以概括就得到数学样条这一概念,最常用三次样条插值函数。
在微积分问世以后,插值法被作为一种逼近函数的构造方法,是函数逼近、数值微积分和微分方程数值解的基础。拉格朗日插值是利用基函数方法构造的插值多项式,在理论上较为重要,但计算不太方便。基函数方法是将插值问题划归为特定条件下容易实现的插值问题,本质上是广义的坐标系方法。牛顿插值多项式计算上较为方便,是求函数近似值常用的方法,尤其是等距节点的差分插值公式最为常用。带导数条件的埃尔米特插值主要掌握构造插值多项式的方法及其余项表达式。由于高次插值存在龙格现象,它没有实用价值,通常使用分段低次插值,特别是三次样条插值,它具有良好的收敛性与稳定性,又有二阶光滑度,理论上和应用上都有重要意义,在计算机图形学中有重要应用。
插值软件一般包含两个程序,一个用于计算插值多项式,另一个用于计算其在任意点或点集上的值。第一个程序的输入数据包括数据点的个数及两个一维数组,分别存储自变量及其对应的函数值,第二个程序输入数据包括需要求值的一个或多个变量的值,输出相应求值点上的函数值。通常可用 MATLAB软件中多项式插值( polyfit),样条插值( spline),样条函数赋值(ppval)。
第三章 函数逼近和快速傅里叶变换FFT
函数逼近是用简单函数逼近复杂函数的问题,是数值分析的基础。考察逼近函数的标准是在某种意义下误差最小。本章讨论用多项式、有理函数和三角多项式逼近数据和函数:
- 多项式逼近着重介绍最佳平方逼近,当被逼近函数可以在任意自变量下计算时(连续),这些逼近就是在整个区间上误差平方和积分,但多项式最佳一致逼近计算困难
- 正交多项式中的勒让德多项式和切比雪夫多项式是两个十分重要且经常使用的正交多项式。
- 当一个函数由给定的一组可能不精确表示函数的数据来确定时(离散),使用最小二乘的曲线拟合是最合适的,它是离散点的最佳平方逼近,当模型为多项式时其法方程是病态的,为此推荐用点集正交化方法可避免解法方程,是目前计算机上常用的算法
- 有理逼近是函数逼近的重要组成部分,本章只介绍帕德逼近
- 如果数据是周期的,使用三角最小二乘或三角插值是合适的,计算用快速傅里叶变换(FFT),它是节省计算量的一个范例。本章介绍的算法是它的一种改进,比原始算法节省一半计算量。
第四章 数值积分与数值微分
积分和微分是两种分析运算,它们都是用极限来定义的。数值积分和数值微分则归结为函数值的四则运算,从而使计算过程可以在计算机上完成处理。数值积分和数值微分的基本方法是逼近法:设法构造某个简单函数P(x)近似f(x),然后对P(x)求积(求导)得到f(x)的积分(导数)的近似值。本章基于插值原理推导了数值积分和数值微分的基本公式。建立求积公式的另一途径是利用代数精度定义,通过解方程得到求积系数。早在1676年牛顿就提出了基于等距节点的插值求积方法,1743年辛普森提出的复合辛普森求积公式一直是计算积分近似值的重要方法,直到1955年由龙贝格利用理查森外推得到了龙贝格求积方法,使等矩节点求积精度进一步提高,龙贝格方法是目前计算机上求积的重要方法,针对被积函数变化不均匀的自适应方法也是以此为基础给出的。另一类不等距节点的求积公式是1814年由高斯首先提出的具有最高代数精度的高斯求积公式,它精度高,稳定性好,还可计算某些奇异积分,是一类减少计算函数值的好方法。
数值积分的软件在 MATLAB库中有quad(一维)及dBlquad(二维)。对数值微分可用diff。
第五章 解线性方程组的直接方法
解线性方程组的直接方法,使用有限步算术运算即可求得方程组的精确解,且仅受舍入误差影响,为减少舍入误差,通常推荐列主元消去法,它减少了舍入误差影响而不增加太多的额外计算。经典的高斯消去法是1810年提出的,它稍作修改产生矩阵的LU分解,则是20世纪40年代才提出的。当A非奇异时只要对A做行置换,总可使PA=LU,其中P为行置换矩阵,利用它求解线性方程组相当于列主元消去法,它的好处是具有相同系数矩阵A的不同向量b的线性方程组Ax=b可节省工作量,当矩阵A对称正定时可用分解的平方根法或改进平方根法,它是计算稳定的。追赶法是解三对角方程组的有效方法,它具有计算量少,方法简单且计算稳定等优点。关于矩阵条件数,病态方程组及算法稳定性也是很重要的,但本章只做简单介绍。
求解线性方程组Ax=b的软件包主要来自 LINPACK和 LAPACK,它们中许多子程序都可用 MATLAB实现,它比传统软件求解简单,命令x=A\b是通过LU分解求得线性方程组的解,也可通过lu函数单独计算LU分解,[L,U]=lu(A),如果A对称正定,可通过L=chol(A)得到分解。
第六章 解线性方程组的迭代法
考虑线性方程组Ax=b,其中A为非奇异矩阵。当A为低阶稠密矩阵时,第5章所讨论的选主元消去法是解此方程组的有效方法。但是,对于由工程技术中产生的大型稀疏矩阵方程组:A的阶数n很大,但零元素较多,例如求某些偏微分方程数值解所产生的线性方程组,n≥10^4,利用迭代法求解线性方程组是合适的。在计算机内存和运算两方面,迭代法通常都可利用A中有大量零元素的特点。迭代法就是逐步带入求近似解,包括雅可比迭代法、高斯-塞德尔迭代法、超松弛迭代法和共轭梯度法。
第七章 非线性方程及方程组的数值解法
本章着重介绍求解单变量非线性方程f(x)=0的迭代法及其理论。不动点迭代、局部收敛性及收敛阶等基本概念,很容易推广到非线性方程组。在迭代法中以牛顿法最实用,它在单根附近具有二阶收敛,但应用时要选取较好的初始近似才能保证迭代收敛。为克服这一缺点,可使用牛顿下山法。斯特芬森方法可将一阶方法加速为二阶。弦截法(或称割线法)与抛物线法(也称密勒法)是属于插值方法,它们不用算f(x)的导数,又具有超线性收敛,这类方法是多点迭代法,它不同于单点迭代,计算时必须给出两个以上的初始近似。
求解单个方程f(x)=0的软件一般要提供函数值f的程序名和误差限及迭代过程判停准则,初始近似或有根区间[a,b]。在 MATLAB中用 fzero计算出初值附近的一个根,而函数roots则用于计算多项式全部零点。非线性方程组解法本章只介绍最基础的方法,其中牛顿迭代法是最常用最重要的方法,很多新方法是以它的变型或改进得到的,如拟牛顿法及Broyden法。求解非线性方程组的库中为函数fsolve。
第八章 矩阵特征值计算
A∈R为非奇异矩阵,则存在正交矩阵Q与上三角矩阵R,QR分解A=QR,舒尔分解。
利用圆盘定理给出特征值的大致估计是很必要的,对特征值的扰动分析本章只给出最基本概念和简单情形的分析。
关于特征值计算本章只给出较常用的两种方法,即幂法、反幂法及QR算法。前两种为迭代法,只求模最大与模最小的特征值及特征向量;最后一种是变换法,可求全部特征值。幂法计算简单,适用于稀疏情形,但收敛速度往往不能令人满意,使用时可结合反幂法及位移技巧等手段加速收敛。本章着重介绍正交变换(豪斯霍尔德变换和吉文斯变换),它是简化矩阵和QR分解的有力工具。将矩阵变换为上海森伯格矩阵,然后用QR方法求全部特征值,是计算中小型矩阵特征值十分有效的方法。关于对称矩阵的特征值计算除本章给出的QR方法和瑞利商加速外还有很多方法,如古老的雅可比方法,兰乔斯方法以及较新的分而治之法。
特征值计算在MATLAB中的函数为[V,D]=eig(A),可以得到一个矩阵A的特征值和完备的特征向量矩阵,并分别存放于对角矩阵D和矩阵V中。
第九章 常微分方程初值问题数值解法
科学技术中很多问题都可用常微分方程的定解问题来描述,主要有初值问题与边值问题两大类。本章只考虑初值问题。常微分方程初值问题中最简单的例子是人口模型:设某特定区域在t。时刻人口y(t。)=y。为已知的,该区域的人口自然增长率为A,人口增长与人口总数成正比,所以t时刻的人口总数y(t)满足微分方程。很多物理系统与时间有关,从卫星运行轨道到单摆运动,从化学反应到物种竞争都是随时间的延续而不断变化的。常微分方程是描述连续变化的数学语言。微分方程的求解就是确定满足给定方程的可微函数y(t),研究它的数值方法是本章的主要目的。
虽然求解常微分方程有各种各样的解析方法,但解析方法只能用来求解一些特殊类型的方程,实际问题中归结出来的微分方程主要靠数值解法。所谓数值解法,就是寻求解y(x)在一系列离散节点x1<x2<…<xn<…上的近似值y1,y2,…,yn,…相邻两个节点的间距h称为步长。本章首先要对常微分方程离散化,建立求数值解的递推公式。一类是计算yn+1时只用到前一点的值yn,称为单步法。另一类是用到yn+1前面k点的值,称为k步法。其次,要研究公式的局部截断误差和阶,数值解与精确解的误差估计及收敛性,还有递推公式的计算稳定性。
在求解微分方程组时,经常出现解的分量数量级差别很大的情形,这给数值求解带来很大困难,这种问题称为刚性问题(stiff)。刚性问题在化学反应、电子网络和自动控制等领域中都是常见的。比如一个解:。求刚性方程数值解时,若用步长受限制的方法就将出现小步长计算大区间的问题,因此最好使用对步长h不加限制的方法,如欧拉后退法及梯形法。
本章研究求解常微分方程初值问题的数值方法,1768年欧拉首先提出了解初值问题的欧拉法,为提高阶数龙格(1895),Heun(1900)和库塔(1901)提出了龙格-库塔法,它是基于泰勒展开形成的单步方法。1883年由阿当姆斯基于数值积分得到的阿当姆斯外插与内插方法是一种多步法,这是构造数值方法的另一途径,但通常利用泰勒展开的构造方法更具一般性,且它在构造多步法公式时可同时得到公式的局部截断误差。由于四阶显示龙格-库塔方法精度高且是自开始的,易于调节步长,且计算稳定,因此是计算机中数学库常用的算法。它的不足之处是计算量较大,且当f(x,y)的光滑性较差时,计算精度可能不如低阶方法。多步法和由它们形成的预测一校正公式,通常每步计算量较少,但它不是自开始的,需要借助四阶龙格一库塔法提供开始值。对数值方法的分析涉及局部截断误差、整体误差、相容性、收敛性和稳定性等概念,特别是绝对稳定性的讨论涉及计算中步长h的选取,本章主要针对单步法进行理论证明,对多步法则只给出相应概念和结论。关于数值方法稳定性理论是20世纪50年代由 Dahlquist研究得到的,本章有关的内容可参看吉尔(Gear)1971年的重要著作。刚性方程组是具有重要应用价值的问题,具体求解有一定困难。
求常微分方程初值问题数值方法的软件在 MATLAB数学库中都有龙格-库塔法,阿当姆斯方法和解刚性方程组的子程序,它们都是针对m个变量的m个一阶方程的方程组,使用时要提供计算任意点x,y上函数值的程序名f,并输入方程个数m,初始值x0,y0和自变量计算到xn的值以及误差限。
PRML中文版_模式识别与机器学习
目录
1 绪论 1.1例子:多项式曲线拟合 1.2概率论 概率密度 期望和协方差 贝叶斯概率 高斯分布 重新考察曲线拟合问题 贝叶斯曲线拟合 1.3模型选择1.4维度灾难1.5决策论 最小化错误分类率 最小化期望损失 拒绝选项 推断和决策 回归问题的损失函数1.6信息论 相对熵和互信息
2 概率分布 2.1二元变量 Beta分布2.2多项式变量 狄利克雷分布 2.3高斯分布 条件高斯分布 边缘高斯分布 高斯变量的贝叶斯定理 高斯分布的最大似然估计 顺序估计 高斯分布的贝叶斯推断 学生t分布 周期变量 混合高斯模型 2.4指数族分布 最大似然与充分统计量 共轭先验 无信息先验 2.5非参数化方法 核密度估计 近邻方法
3 回归的线性模型 3.1线性基函数模型 最大似然与最小平方 最小平方的几何描述 顺序学习 正则化最小平方 多个输出 3.2偏置·方差分解 3.3贝叶斯线性回归 参数分布 预测分布 等价核 3.4贝叶斯模型比较 3.5证据近似 计算证据函数 最大化证据函数 参数的有效数量 3.6固定基函数的局限性
4 分类的线性模型 4.1判别函数 二分类 多分类 用于分类的最小平方方法 Fisher线性判别函数 与最小平方的关系 多分类的Fisher判别函数 感知器算法 4.2概率生成式模型 连续输入 最大似然解 离散特征 指数族分布 4.3概率判别式模型 固定基函数 logistic回归 选代重加权最小平方 多类logistic回归 probit回归 标准链接函数 4.4拉普拉斯近似 模型比较和BIC 4.5贝叶斯 logistic回归 拉普拉斯近似 预测分布
5 5.1前馈神经网络 权空间对称性 5.2 网络训练 参数最优化 局部二次近似 梯度下降最优化 5.3误差反向传播 误差函数导数的计算 反向传播的效率 Jacobian矩阵 5.4 Hessian矩阵 对角近似 外积近似Hessian矩阵的逆矩阵 有限差 Hessian矩阵的精确计算 Hessian矩阵的快速乘法 5.5神经网络的正则化 相容的高斯先验 早停止 不变性 切线传播 用变换后的数据训练 卷积神经网络 软权值共享 5.6混合密度网络 5.7贝叶斯神经网络 后验参数分布 超参数最优化 用于分类的贝叶斯神经网络
6 核方法 6.1对偶表示 6.2构造核 6.3径向基函数网络 Nadaraya- Watson模型 6.4高斯过程 重新考虑线性回归问题 用于回归的高斯过程 学习超参数 自动相关性确定 用于分类的高斯过程 拉普拉斯近似 与神经网络的联系
7 稀疏核机 7.1最大边缘分类器 重叠类分布 与 logistic回归的关系 多类SVM 回归问題的SVM 计算学习理论 7.2相关向量机 用于回归的RVM 稀疏性分析 RVM用于分类
8 图模型 8.1贝叶斯网络 例子:多项式回归 生成式模型 离散变量 线性高斯模型 8.2条件独立 图的三个例子 d-划分 8.3马尔科夫随机场 条件独立性质 分解性质 例子:图像去噪 与有向图的关系 8.4图模型中的推断 链推断 树 因子图 加和乘积算法 最大加和算法 一般图的精确推断 循环置信传播 学习图结构
9 混合模型和EM 9.1 K均值聚类 图像分割与压缩 9.2混合高斯 最大似然 用于高斯混合模型的EM 9.3EM的另一种观点 重新考察高斯混合模型, 与K均值的关系 伯努利分布的混合 贝叶斯线性回归的EM算法 9.4一般形式的EM算法
10 近似推断 10.1变分推断 分解概率分布 分解近似的性质 例子:一元高斯分布 模型比较 10.2例子:高斯的变分混合 变分分布 变分下界 预测概率密度确定分量的数量 诱导分解 10.3变分线性回归 变分分布 预测分布 下界 10.4指数族分布 变分信息传递 10.5局部变分方法 10.6变分logistic回归 变分后验概率分布 最优化变分参数 超参数的推断 10.7期望传播 例子:聚类问题 图的期望传播
11 采样方法 11.1基本采样算法 标准概率分布 拒绝采样 可调节的拒绝采样 重要采样 采样-重要性-重采样 采样与EM算法 11.2马尔科夫链蒙特卡罗 马尔科夫链 Metropolis-hastings算法 11.3吉布斯采样 11.4切片采样 11.5混合蒙特卡罗算法 动态系统 混合蒙特卡罗方法11.6 估计划分函数
12 连续潜在变量 12.1主成分分析 最大方差形式 最小误差形式 PCA的应用 高维数据的PCA 12.2概率PCA 最大似然PCA 用于PCA的EM算法 贝叶斯PCA 因子分析 12.3核PCA 12.4非线性隐含变量模型 独立成分分析 自关联网络 对非线性流形建模
13 顺序数据 13.1马尔科夫模型 13.2隐马尔科夫模型 用于HMM的最大似然法 前向后向算法 用于HMM的加和乘积算法 缩放因子 维特比算法 隐马尔科夫模型的扩展 13.3线性动态系统 LDS中的推断 LDS中的学习 LDS的推广 粒子滤波
14 组合模型 14.1贝叶斯模型平均 14.2委员会 14.3提升方法 最小化指数误差 提升方法的误差函数14.4基于树的模型 14.5条件混合模型 线性回归模型的混合 14.6logistic模型的混合专家混合
欧拉公式
复平面内一个单位圆上的点,当与实轴夹角为 θ 时,此点用函数可表示为e^jθ 。
欧拉公式: 。
做圆周运动,若运动角速度为
,

泰勒公式
如果f(x)在包含 的某个开区间(a,b)内具有直到(n+1)阶的导数,则对于任何在(a,b)间x,f(x)按
的幂展开的n阶泰勒公式:
其中余项,
介于x和x0之间。
当x0=0时,麦克劳林公式:
对数和幂
如果a的x次方等于N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作x=loga N。其中,a叫做对数的底数,N叫做真数。自然对数是以无理数e为底的对数,记为lnN。以10为底的对数,记为lgN。
卷积
在现实中,卷积代表的是将一种信号搬移到另一频率中。比如调制。这是频率卷
从数学看,卷积是一种反映两个序列或函数之间的运算方法;
从物理上看,卷积可代表某种系统对某个物理量或输入的调制或污染;
从信号角度来看,卷积代表了线性系统对输入信号的响应方式。无论在离散时间或连续时间情况下,单位冲激函数的重要特性之一就是一般信号都可以表示为延迟冲激的线性组合。这个事实,再与叠加性和时不变性结合,就能够用LTI的单位冲激响应来完全表征任何一个LTI系统的特性。这样一种表示——在离散时间情况下称为卷积和,在连续时间下称为卷积积分——在分析LTI系统时提供了极大的方便性。 (奥本海默第二章)
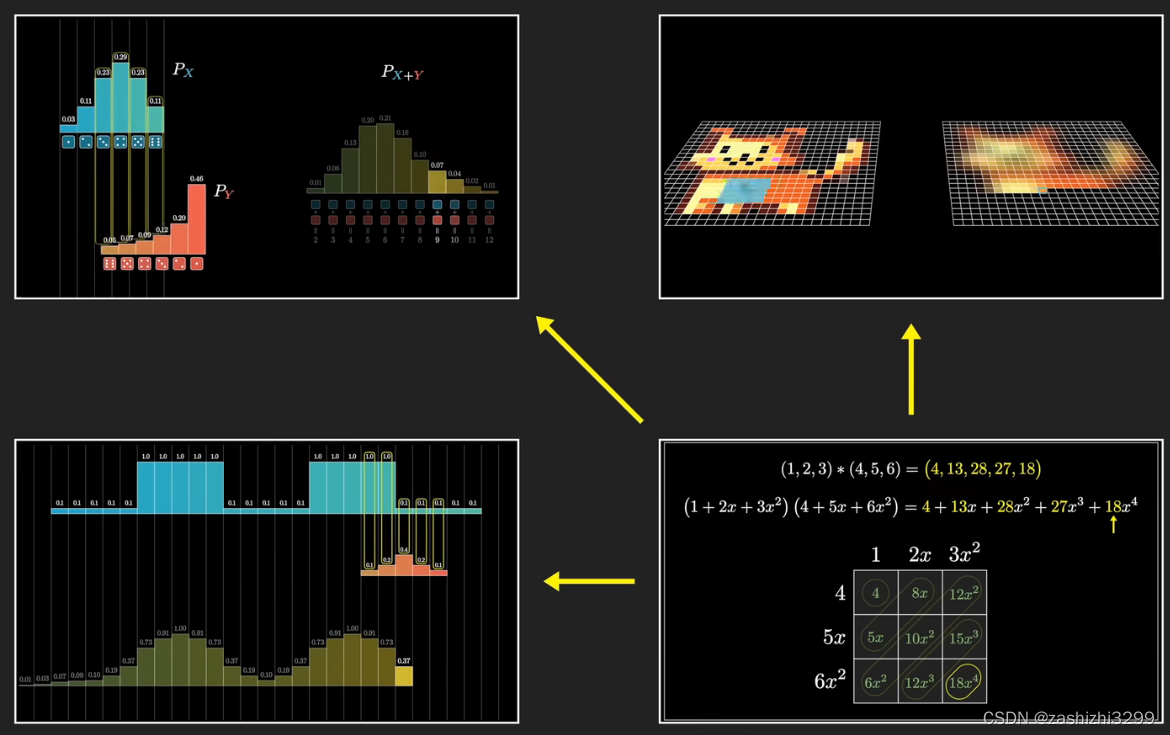


数学:两个序列(一维数组、二维矩阵)卷积,其本质反转平移。乘法可以看成是每个位的卷积,当两个数非常大(n位)的时候,卷积比乘法的计算复杂度小很多,从减少到
数学应用:多项式系数,两个函数乘积的系数;
概率应用:如图;
图像处理应用:模糊图像,边缘检测;
线性代数:系数和方程解的关系;
以离散信号为例,说明卷积的含义。
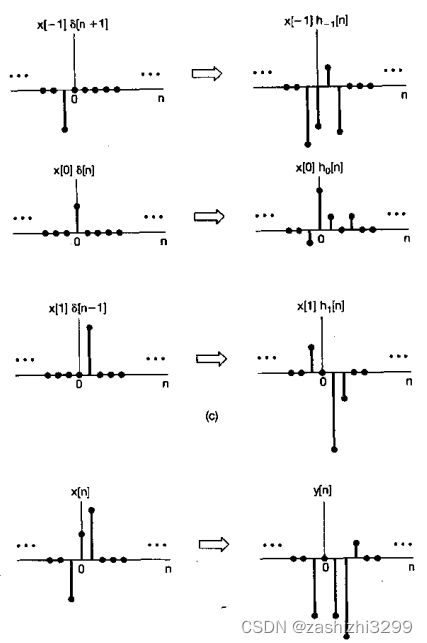
第一步:如何把任何离散时间信号看成是由离散时问单位脉冲构成的关键是:要把个离散时问信号当作一串单个的脉冲来想象。如一个离散信号
即
这个式子相应于把任意序列表示成一串移位的单位脉冲序列的线性组合,线性组合的加权因子就是
。公式反应了离散脉冲序列的筛选性质,因为
当且仅当k=n时非0,筛选出此刻的
。
第二步:一个LTI系统对x[n]的响应y[n]就是,系统对每一个脉冲序列的响应
的和。
公式右边就是卷积和,记作:
任意输入x[n]的响应都可以用系统对单位脉冲的响应来表示,那么LTI系统的单位脉冲响应就完全刻画了系统的特性。
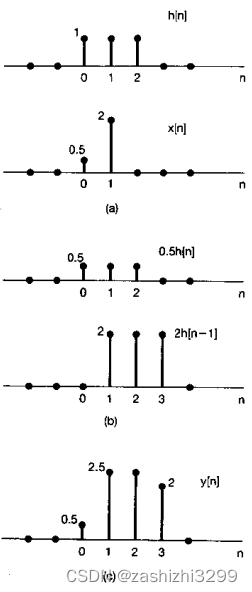
例1:已知x[n] 和h[n-k],求y[n]

按卷积和公式,分别求x[k]的响应,再叠加。
例2:已知x[n] 和h[n],求y[n]。对某个特定的n值求y[n]。
如左图,和例1不同,给出h[n],平移得到h[n-1]。
再看例1,给出h[n-1]并不是h[n-0]右移一位得到的?这就是k的反转平移。不是n的反转平移。
现在具体考虑一下对某个特定的n值求y[n]的问题。一开始就将信号x[k]和h[n-k]都看成k的函数,将它们相乘就得到序列g[k]=x[k]h[n-k],它可看作在每一个时刻k,输入x[k]对输出在时刻n作出的贡献,这样就能得出如下结论:将全部g[k]序列中的样本值相加就是在所选定的时刻n的输出值。由此,为了对y[n]计算出全部n时的值,就需要对每个n值重复这一过程。所幸的是,对x[k]和h[n-k],将它们看作是k的函数,改变n值可以有一个非常简单的图解表示,如下右图。h[n-k]就是对h[k]的反转平移。先k反转-k,再平移n。对于任何具体的n,画出h[n-k]。计算x[k]和h[n-k]的乘积,然后在所有的k上把乘积相加。对于本例,图中看出,当n<0,x[k]和h[n-k]的非0值都不重合,即乘积都为0;在n=0重合一个k=0点;在n=1重合2个点k=0和1;在n=2重合2个点k=0和1;在n=3重合一个k=1点;当n>3,都不重合,即乘积都为0。

卷积的应用
1、图像处理:图像处理中常见的mask运算都是卷积,广泛应用于图像滤波。卷积有平滑效应和展宽效应。
一维卷积:y(t)=g(k)*x(k)=$g(k)x(t-k) ,先把函数x(k)相对于原点反折,然后向右移动距离t,然后两个函数相乘再积分,就得到了在t处的输出。对每个t值重复上述过程,就得到了输出曲线。
二维卷积:h(x,y)=f(u,v)*g(u,v)=$$f(u,v)g(x-u,y-v) ,先将g(u,v)绕其原点旋转180度,然后平移其原点,u轴上像上平移x, v轴上像上平移y。然后两个函数相乘积分,得到一个点处的输出。
图像处理中的卷积与上面的定义稍微有一点不同。用一个模板和一幅图像进行卷积,对于图像上的一个点,让模板的原点和该点重合,然后模板上的点和图像上对应的 点相乘,然后各点的积相加,就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的,所以模板不旋转。
把一个点的像素值用它周围的点的像素值的加权平均代替。
2、信号处理:卷积关系最重要的一种情况,就是在信号与线性系统(如求电路响应)或数字信号处理中的卷积定理。利用该定理,可以将时间域或空间域中的卷积运算等价为频率域的相乘运算,从而利用FFT等快速算法,实现有效的计算,节省运算代价。1)卷积实质上是对信号进行滤波;2)卷积就是用冲击函数表示激励函数,然后根据冲击响应求解系统的零状态响应。卷积是求和(积分)。对于线性时不变的系统,输入可以分解成很多强度不同的冲激的和的形式(对于时域就是积分),输出也就是这些冲激分别作用到系统产生的响应的和(或者积分)。所以卷积的物理意义就是表达了时域中输入、系统冲激响应、输出之间的关系。信号处理的任务就是寻找和信号集合对应的一个集合,然后在另外一个集合中分析信号,Fourier变换就是一种,它建立了时域中每个信号函数与频域中的每个频谱函数的一一对应关系,这是元素之间的对应。另外还有运算之间的对应,在时域的加法对应频域中的加法,这就是FT线性性的体现;时域的乘法对应,最后得到的那个表达式我们就把它叫卷积,就是对应的频域的卷积。
信号处理是将一个信号空间映射到另外一个信号空间,通常就是时域到频域,(还有z域,s域),信号的能量就是信号函数的范数,Paserval定理就是说映射前后范数不变,在数学中就叫保范映射。实际上信号处理中的变换基本都是保范映射,只要Paserval定理成立就是 保范映射(就是能量不变的映射)。
3、数学:序列、多项式、矩阵与卷积的关系。卷积是人为定义的一种运算,就是为了计算的方便规定的一种两个函数的特殊乘法,或者是一种反映两个序列或函数之间的运算方法。对离散序列来说就是两个多项式的乘法,多项式相乘,相当于系数向量的卷积。物理意义就是冲激响应的线性叠加,所谓冲激响应可以看作是一个函数,另一个函数按冲激信号正交展开。称(f*g)(n)为f,g的卷积:
连续:
离散:
简单来说,卷积是一种重叠关系,也就是说,所得到的结果反映了两个卷积函数的重叠部分。所以,用一个已知频段的函数卷积另一个频段很宽的函数,也就是对后者进行了滤波,后者跟前者重叠的频段才能很好地通过这个filter。
两个函数普通乘积的积分变换(傅里叶变换与拉普拉斯变换)与这两个函数积分变换的卷积建立了关系,使我们只要会求两个函数的变换,利用卷积就可以求这两个函数乘积的变换。傅立叶变换最重要的应用之一就是可以将卷积方程变成两个函数的乘积形式去求解。
离散卷积的例子:丢骰子,两枚骰子f和g点数加起来为4的概率是多少?
f(i)表示点数为i的概率。两枚骰子点数加起来为4的概率为:f(1)g(3)+f(2)g(2)+f(3)g(1),符合卷积的定义,把它写成标准的形式就是:
LTI系统与卷积与傅里叶变换
正如在3.0节已经指出的,在研究LTI系统时,将信号表示成基本信号的线性组合是很有利的,但这些基本信号应该具有以下两个性质:
- 由这些基本信号能够构成相当广泛的一类有用信号;
- LTI系统对每一个基本信号的响应应该十分简单,以使得系统对任意输入信号的响应有一个很方便的表示式。
总结两步:1、知道y(t)的表达式(卷积);2、分解x(t)(傅里叶)
傅里叶分析的很多重要价值都来自于这一点,即连续和离散时间复指数信号集都具有上述两个性质,即连续时间的和离散时间的
信号,其中s和z都是复数(纯虚数,若有实部则上升为拉氏变换)。第二个性质说明在LTI系统分析中为什么要应用傅里叶级数和傅里叶变换的缘由。
LTI系统的响应=特征值×特征函数=H(s).
以连续函数响应为例,根据卷积公式:
例:若,
那么通过计算特征函数的s值,再计算H(s)可以得到:
s的值可以通过欧拉公式分解x(t)得到:
如果x(t)更复杂,无法通过欧拉公式分解成的线性组合,那么就需要傅里叶变换。
傅里叶级数
在信号与系统中,任何(连续、离散)的周期信号都可以表示为复指数信号组合的形式,这些复指数信号成谐波关系。组合称为为傅里叶级数。傅里叶级数最重要的性质之一是复指数特征函数性质,这就是:若一个周期信号加到一个LTI线性时不变系统上,那么输出也一定是周期的,且与输入信号的周期相同;并且输出的每一个傅里叶系数就是对应的输入傅里叶系数乘以复指数,该复指数的值是相应于傅里叶系数的那个频率的函数。这一频率函数是该LTI系统的表征,称之为该系统的频率响应。通过考察系统的频率响应,推出利用LTI系统对信号进行过滤的思想。一个重要的应用是有关频率选择性滤波的概念,也就是利用LTI系统通过某些给定频带的频率,而阻止或显著衰减掉其余频率的概念。
连续周期信号傅里叶级数:,
离散周期信号傅里叶级数:,
时域函数展开傅里叶级数,在频域上得到组成该周期函数的所有三角函数的频率。
例:推导连续周期函数的傅里叶级数的系数
两边同时乘:
两边在0-T内积分:
右边积分部分:
得到:
傅里叶变换
把傅里叶级数概念推广应用到非周期信号中去。将会看到,有限能量的非周期信号也能够经由复指数信号的线性组合来表示。对周期信号而言,这些复指数基本信号构造单元全是成谐波关系的;而对非周期信号,它们则是在频率上无限小地靠近的。因此,作为线性组合表示所取的形式是一谐波关系个积分,而不是求和。在这种表示中所得到的系数谱称为傅里叶变换;而利用这些系数将信号表示为复指数信号线性组合的综合积分式本身则称之为傅里叶反变换。傅里叶认为一个非周期信号能够看成是周期无限大的周期信号。更加确切些就是,在一个周期信号的傅里叶级数表示中,当周期增加时,基波频率就减小,成谐波关系的各分量在频率上愈趋靠近;当周期变成无穷大时,这些频率分量就形成了一个连续域,从而傅里叶级数的求和也就变成了一个积分。
傅里叶变换重要性质:
- 第一是卷积性质。卷积是一种积分运算,它可以用来描述LTI的输入和输出的关系:输出可以通过输入和一个表征系统特性的函数(冲激响应函数)进行卷积运算得到。
。它将两个信号的卷积映射为他们傅里叶变换的乘积。h(t)完全表征了一个LTI系统,H(jw)也一样,这种表征是用频域的方法来分析LTI系统的基础。其中H(jw)是单位冲激响应h(t)的傅里叶变换,它控制着每一个频率w上输入的傅里叶变换复振幅的大小,应用比如通过控制H的值在0到1之间来滤波。
- 第二是相乘性质,它是频域分析方法研究采样和调制系统的基础。
连续非周期信号傅里叶变换:
反变换:
离散非周期信号傅里叶变换:
反变换:
拉普拉斯变换
连续傅里叶变换提供了将信号表示成形如的复指数信号的线性组合;然而,由3.2节引入的特征函数性质及其它的很多结果对任意s值都是适用的,而并不是将它仅限于纯虚数的情况,连续时间傅里叶变换的推广,称之为拉普拉斯变换。对应的离散傅里叶变换的推广,称之为z变换。拉普拉斯变换和z变换都有很多使傅里叶变换的性质,在一些傅里叶变换不能应用的重要方面,它们也能够应用。例如:拉普拉斯变换和z变换能用于许多不稳定系统的分析。这一事实再与拉普拉斯变换和z变换与傅里叶变换的代数性质结合,就形成了一整套重要的系统分析工具,尤其是在反愦系统分析中更是如此。
拉普拉斯变换:
反变换:
一句话说明拉普拉斯变换与傅里叶变换异同:
傅里叶变换看到函数中存在哪些sinusoidal三角函数;
拉普拉斯变换看到函数中除了三角函数,还包指数函数exponential;
傅氏变换是拉氏变换的一部分。
从公式看:
的拉普拉斯变换也就是
的傅里叶变换,对于所有实数
都做一次傅里叶变换,即可获得整个拉普拉斯变换。

例:函数的傅里叶变换和拉普拉斯变换。

解:
对于傅氏变换,一个输入维度:虚数,两个输出维度:实部和虚部。可以用3D图绘制
对于拉氏变换,两个输入维度:实数和虚数
,两个输出维度:实部和虚部。
当时,拉氏变换就是傅氏变换。绘制拉氏变换图,计算几个输入和输出:
傅氏变换如下图。左图输入坐标轴只有虚轴代表
变化,右图是一个等高线图,相当于从上往下看,看到的只有输入的虚轴,横轴代表
,纵轴表示
。此图丢失了
的实部虚部分别的数值,只留下它的模。
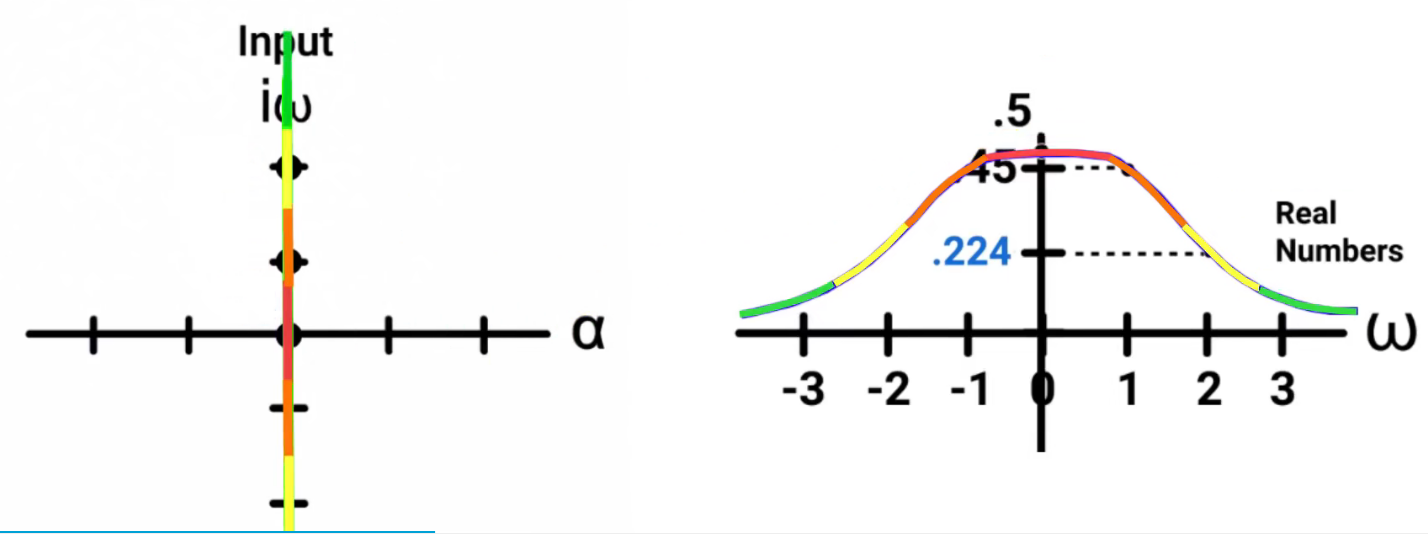
当, 对于所有实数
都做一次
的傅里叶变换,即可获得整个拉普拉斯变换。
拉氏变换如下右图,x轴为
,y轴为
,z轴为
。
对某个对此拉氏图做切面,映射在zoy平面上的曲线就是相应的傅氏变换。
注意到xoy平面有两个窟窿,此时,
分母为0,此处为“极点”,此处拉氏变换不存在。

对于任何函数,决定周期大小sinusoidal,离原点越远频率越大;
决定衰减程度exponential,离原点越远衰减越大。
例:弹簧简谐运动。
解:这个运动两部分叠加:无阻尼弹簧的简谐振动 和 阻尼衰减运动。
弹簧简谐运动证明如下,变量t时间,拉力(铁块自重m),弹簧形变长度s。
(胡克定律);
(牛顿第二定律);
(
为合并后常量)
结论:弹簧形变长度s随着时间t做(正弦)简谐运动。
再加入阻尼运动得到运动方程:弹簧瞬时拉力+阻尼+弹簧形变力=铁块重力(外部输入)

两边做Laplace变换,忽略初始条件:

得到系统的(辅助)特征方程 ,从特征方程可以得到很多系统特征信息,比如零极点。

在时域不好解决的问题,用拉氏变换转换到复频域的代数问题。
数据分析与可视化图
Matplotlib库中的50个数据分析图,共分为7大类:Correlation、Deviation、RankIng、Distribution、Composition、Change、Groups:
- Correlation 相关性:Scatter plot(散点图)Bubble plot with Encircling(包围的气泡图)Scatter plot with linear regression line of best fit(散点图与最佳线性拟合回归线)Jittering with stripplot(带条纹的抖动)Counts Plot(计数图)Marginal Histogram(边缘直方图)Marginal Boxplot(边缘箱线图)Correllogram(相关图)Pairwise Plot(成对图)
- Deviation 偏差:Diverging Bars(发散条形图)Diverging Texts(发散文本)Diverging Dot Plot(散点图)Diverging Lollipop Chart with Markers(带标记的发散型棒棒糖图)Area Chart(面积图)
- Ranking 排序:Ordered Bar Chart(有序条形图)Lollipop Chart(棒棒糖图)Dot Plot(点图)Slope Chart(坡度图)Dumbbell Plot(哑铃图)
- Distribution 分布:Histogram for Continuous Variable(连续变量的直方图)Histogram for Categorical Variable(类型变量的直方图)Density Plot(密度图)Density Curves with Histogram(直方密度图) Joy Plot(标记图)Distributed Dot Plot(分布式点图)Box Plot(箱形图)Dot + Box Plot(点+箱型图)Violin Plot(小提琴图)Population Pyramid(人口金字塔)Categorical Plots(分类图)
- Composition 组成:Waffle Chart(华夫饼表)Pie Chart(饼状图)Treemap(树状图)Bar Chart(条形图)
- Change 变化:Time Series Plot(时间序列图)Time Series with Peaks and Troughs Annotated(带波峰波谷标记的时序图) Autocorrelation (ACF) and Partial Autocorrelation (PACF) Plot(自相关和部分自相关图)Cross Correlation plot(交叉相关图)Time Series Decomposition Plot(时间序列分解图)Multiple Time Series(多时间序列)Plotting with different scales using secondary Y axis(使用辅助Y轴来绘制不同范围的图形)Time Series with Error Bands(带有误差带的时间序列)Stacked Area Chart(堆积面积图)Area Chart UnStacked(未堆积的面积图)Calendar Heat Map(日历热力图)Seasonal Plot(季度图)
- Groups:Dendrogram(树状图)Cluster Plot(簇状图)Andrews Curve(安德鲁斯曲线)Parallel Coordinates(平行坐标)
参考文献:
1、《计算统计-[美]Geof H.Givens-人民邮电出版社-2009》
2、《数值分析_李庆扬_第五版》
3、《 概率论基础教程_Sheldon M.Ross》
4、拉普拉斯变换真正告诉我们什么 - 视觉解释_哔哩哔哩_bilibili https://www.bilibili.com/video/BV1Gh411t7Jy?spm_id_from=333.999.0.0
5、《奥本海默_信号与系统(第二版)》
6、50个最有用的Matplotlib数据分析与可视化图_10点43的博客-CSDN博客_matplotlib相关性分析 https://blog.csdn.net/cg129054036/article/details/106911101
7、
8、卷积的本质及物理意义(全面理解卷积)_彼岸花-CSDN博客_卷积的物理意义
9、最容易理解的对卷积(convolution)的解释_bitcarmanlee的博客-CSDN博客_卷积 https://blog.csdn.net/bitcarmanlee/article/details/54729807
10、【官方双语】那么……什么是卷积?_哔哩哔哩_bilibili https://www.bilibili.com/video/BV1Vd4y1e7pj/?spm_id_from=444.41.list.card_archive.click&vd_source=28b3868c0af23aa93c8a1590fa7a0ae1
11、
12、
13、
14、
15、
16、























 5278
5278

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








