向量基础

<script src="http://widgets.amung.us/classic.js" type="text/javascript"></script> <script type="text/javascript"> </script>

向量基础

 

定义

n维向量：一组n维实数。

 

标记

：表示n维向量

行向量：

列向量：

 

 

注意：

1. 向量是一个包含大小和方向的量。

2. 向量可以用来表示力，速度，位移等等。

3. 向量是各类工程问题的关键。

 

向量和标量的乘法

k：常量(标量)

 

 

向量的单位化

任何一个非零的向量都可以除以它的大小来转化成长度为1的单位向量。

 

举个列子：

 

 

 

向量模(大小，长度)的性质

 

 常数     向量

 

(a) 

(b) 

(c) 

(d) 

 

性质(d)的几何意义：

 

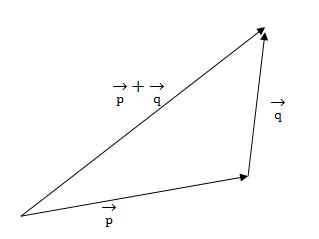
向量的内积(点乘)

例如：

那么它们的内积就是

 

注意：

(a)  内积后的结果是一个常数。

(b)  内积可以表示为矩阵的乘法。如下

 

定理

1.

2. 如果两个向量垂直，那么他们的内积等于零。反之亦然。

 

性质

(a) 

(b) 

(c) 

(d) 

(e) 

 

向量的投影

 

 

1.  在上的投影的长度：

 

2.  在方向上的单位长度：

 

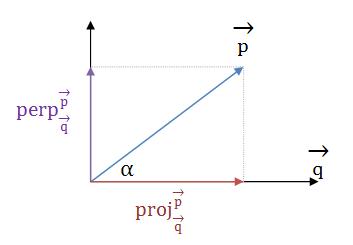
由上面的2个式子可以得到

由向量的加法又有：

 

向量的外积

 

如果有

那么

 

也可以表示为下面的形式

 

定理

 

向量外积的几何意义

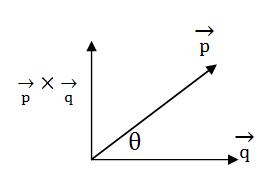
从上图中可以看出，向量的外积也是个向量，并且垂直于进行外积运算的2个向量组成的平面。

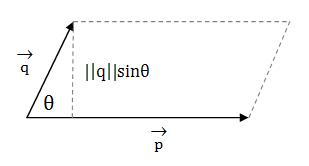
从上图可以看到，这个平行四边形的面积

于是，可以根据这种几何性质计算出已知3个顶点坐标的三角形的面积，如下图

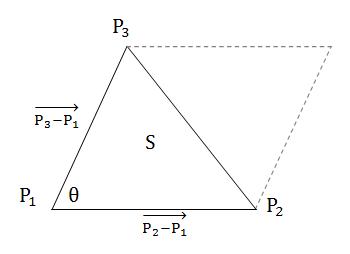
于是得到三角形的面积S

 

右手法则

令

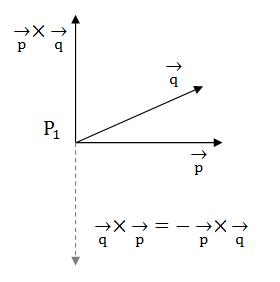
那么

 

外积的性质

(a) 

(b) 

(c) 

(d) 

 

向量空间

 

向量空间是向量的集合，这些向量不仅满足向量的加法和标量乘法，还要满足下面的条件。

1.   (V是向量空间)

2.  存在"0"向量，使得：

3. 

4. 

5. 

 

线性组合

 

一组向量的加法和标量乘法的组合成为线性组合。

 

如果

那么称这些向量线性独立。

 

如果任意一个向量可以用一组向量线性表出如下

那么称为向量基。n是向量基的维数。如果向量基中所有向量的都是单位向量且两两相交，那么该向量基成为正交基。

 

原创文章，转载请注明出处