Discrete Derivative

---

前言

在Simulink中，经常会遇到求导的问题。例如：在车辆动力学建模中，已知了速度，求加速度。
加速度，是速度对时间t的导数，也就是对速度求导，那如何对速度进行求导呢？那就要用到Discrete Derivative模块

---

一、Discrete Derivative

Discrete Derivative的官方解释是：计算离散时间导数。意思就是：求离散时间信号的导数，即信号在离散时间采样点之间的变化速率。公式如下：

其中
y(tn)是当前时间输出
u(tn)和u(tn-1)是当时时间和上一时刻的输入
Ts是模型的仿真步长(定步长，固定值)
K是一个增益量（一般令K=1）

二、建模

1.搭建模型

模型如下

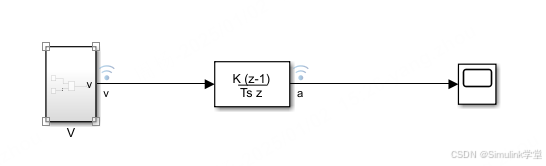
子系统V仿真的是速度随时间的变化，v=2t，在求导得出速度。分别记录速度和加速度的图像，使用Data Inspector来进行分析。
模型求解器设置如下：定步长，离散型，仿真步长为0.002，Stop time=0.2s。
仿真结果
图1

图2

2.分析数据

速度随时间是按照2的倍数变化，所以速度的变化量为2，Ts=0.002，按照y(tn)计算公式，速度的变化率为1000。
但是，我们也能发现，在第一个步长时间内，速度发生了突变，这是我们在实际建模中必须要考虑的问题。关于如何处理速度发生突变的问题，会引出滤波，在下一篇博客会解决这个问题。

---

总结

以上就是今天要讲的内容，本文介绍了Discrete Derivative的使用以及实际存在的缺陷，后期会针对这个问题给出解决方案。