Matrix类的变形方法,最终都是根据用户给出的参数修改内部矩阵。这些方法的不同之处,在于修改值的算法,以及修改结果在矩阵中的位置。
当用户在代码中调用translate(5,13)时,AS3修改矩阵类的内建矩阵,将其中的(tx,ty)T与(5,13)T相加,由于在矩阵创建时(tx,ty)被初始化为(0,0),所以这个结果就是向量(tx,ty)与(5,13)的和。
这个过程如图所示:
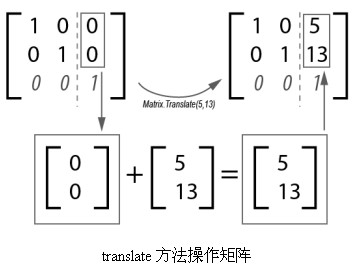
当使用非位移的变换时,这个过程有所改变。根据公式f(x)=Ax+b可知,位移变换是矩阵相加运算,而非位移的变换是矩阵相乘运算。这个过程用代码可以很清晰地展现,新建项目并在代码编辑器中写入以下代码:
var myMatrix:Matrix=new Matrix;
trace(myMatrix.toString());
myMatrix.scale(4,6);
trace(myMatrix.toString());
myMatrix.scale(2,1);
trace(myMatrix.toString());
本例的操作过程如图:
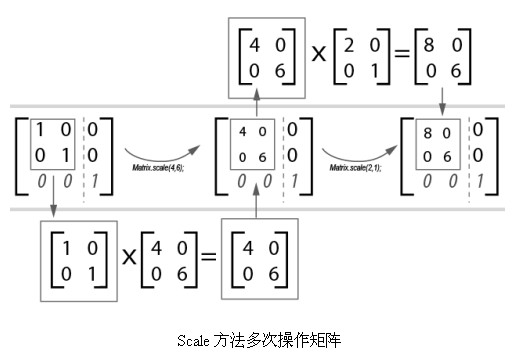
运行,可以观察到输出的结果是:
(a=1, b=0, c=0, d=1, tx=0, ty=0)
(a=4, b=0, c=0, d=6, tx=0, ty=0)
(a=8, b=0, c=0, d=6, tx=0, ty=0)
用这种方法,用户可以研究矩阵类所有方法的内部逻辑。
其实,矩阵类其他内建变形方法的矩阵操作及其图形学算法都大同小异,其通用模式是:
(1)根据方法的类型,对参数进行数学运算
(2)将运算得出的值,赋予变换矩阵中的相应元素
不同的变换有不同的算法和相关矩阵元素,详情可以参考表:
表内建方法的矩阵操作和算法
| 名称 | 详情 |
| translate(tx, ty) |
|
| scale(sx, sy) |
|
| rotate(q) |
|
由此可知,Matrix类的所有内建变形方法都不神秘。它们仅仅是简化了操作,避免了繁琐的操作步骤。例如rotate(q)方法,如果使用此方法,用户只需要一个语句就能完成操作:
DisplayObjectMatrix.rotate(Math.PI/4);
如果不使用这个方法,直接根据其内部机制,操作Matrix类的内部属性,也能达到相同的结果,但步骤显然要繁琐一些:
DisplayObjectMatrix.a=Math.cos(Math.PI/4);
DisplayObjectMatrix.b = Math.sin(Math.PI/4);
DisplayObjectMatrix.c = Math.-sin(Math.PI/4);
DisplayObjectMatrix.d = Math.cos(Math.PI/4);
在动画中经常会要求创建一些复杂的动画变形,但使用Matrix类的内建方法的默认行为,在有些场合并不合适。对于初级用户,因为不具备矩阵知识,面对这种需求只能束手无策。通过前面几小节的学习,原本看似高深莫测的Matrix类,现在已经一目了然不在话下。有了坚实的知识储备,就能根据Matrix和仿射变换矩阵的原理,手工改变各种内建方法的行为,以及根据所需创建其他变换。下一节,将详细讨论如何利用旋转变形制作复杂的动画。























 599
599

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








