协方差矩阵和散布矩阵(散度矩阵)的意义
在机器学习模式识别相关算法中,经常需要求样本的协方差矩阵C和散布矩阵S。如在PCA主成分分析中,就需要计算样本的散度矩阵,而有的教材资料是计算协方差矩阵。实质上协方差矩阵和散度矩阵的意义就是一样的,散布矩阵(散度矩阵)前乘以系数1/(n-1)就可以得到协方差矩阵了。
在模式识别的教程中,散布矩阵也称为散度矩阵,有的也称为类内离散度矩阵或者类内离差阵,用一个等式关系可表示为:
关系:散度矩阵=类内离散度矩阵=类内离差阵=协方差矩阵×(n-1)
样本的协方差矩阵乘以n-1倍即为散布矩阵,n表示样本的个数,散布矩阵的大小由特征维数d决定,是一个为d×d 的半正定矩阵。
一、协方差矩阵的基础
对于二维随机变量(X,Y)之间的相互关系的数字特征,我们用协方差来描述,记为Cov(X,Y):
那么二维随机变量(X,Y)的协方差矩阵,为:
对于三维随机变量X=(X1, X2, X3)的协方差矩阵可表示为:
对于n维X=(X1, X2....X n)协方差矩阵:
需要特别说明的是:
(1)协方差矩阵是一个对称矩阵,且是半正定矩阵,主对角线是各个随机变量 的方差(各个维度上的方差)。
(2)标准差和方差一般是用来描述一维数据的;对于多维情况,而协方差是用于描述任意两维数据之间的关系,一般用协方差矩阵来表示。因此协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。
(3)协方差计算过程可简述为:先求各个分量的均值E(Xi)和E(Xj),然后每个分量减去各自的均值得到两条向量,在进行内积运算,然后求内积后的总和,最后把总和除以n-1。
例子:设有8个样本数据,每个样本有2个特征:(1,2);(3 3);(3 5);(5 4);(5 6);(6 5);(8 7);(9 8),那么可以看作二维的随机变量(X,Y),即
X =[1 3 3 5 5 6 8 9]
Y =[2 3 5 4 6 5 7 8]
Matlab中可以使用cov(X, Y)函数计算样本的协方差矩阵,其中X,Y都是特征向量。当然若用X 表示样本的矩阵(X中每一行表示一个样本,每列是一个特征),那么可直接使用cov(X)计算了。
运行结果为: 当然,可以按定义计算,Matlab代码如下:clear all
clc
X=[1,2;3 3;3 5;5 4;5 6;6 5;8 7;9 8] %样本矩阵:8个样本,每个样本2个特征
covX= cov(X) %使用cov函数求协方差矩阵
%% (1)使用分量的方法,先求协方差c,再组合成协方差矩阵C
meanX=mean(X) %样本均值
varX=var(X) %样本方差
[Row Col]=size(X);
dimNum=Row; %s样本个数size(X,1)=8
dim1=X(:,1); %特征分量1
dim2=X(:,2); %而在分量2
c11=sum( (dim1-mean(dim1)) .* (dim1-mean(dim1)) ) / ( dimNum-1 );
c21=sum( (dim2-mean(dim2)) .* (dim1-mean(dim1)) ) / ( dimNum-1 );
c12=sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( dimNum-1 );
c22=sum( (dim2-mean(dim2)) .* (dim2-mean(dim2)) ) / ( dimNum-1 );
C22=[c11,c12;c21,c22]%协方差矩阵
%% 或者(2)直接求协方差矩阵C
tempX= repmat(meanX,Row,1);
C22=(X-tempX)'*(X-tempX)/(dimNum-1)covX =
7.1429 4.8571
4.8571 4.0000
meanX =
5 5
varX =
7.1429 4.0000
C22 =
7.1429 4.8571
4.8571 4.0000
C22 =
7.1429 4.8571
4.8571 4.0000
二、协方差矩阵的几何意义
为了更好理解协方差矩阵的几何意义,下面以二维正态分布图为例(假设样本服从二维正态分布):
协方差矩阵C的特征值D和特征向量V分别为:
说明:
1)均值[0,0]代表正态分布的中心点,方差代表其分布的形状。
2)协方差矩阵C的最大特征值D对应的特征向量V指向样本分布的主轴方向。例如,最大特征值D1=5对应的特征向量V1=[1 0]T即为样本分布的主轴方向(一般认为是数据的传播方向)。次大特征值D2=1对应的特征向量V2=[0 1]T,即为样本分布的短轴方向。

协方差矩阵C的特征值D和特征向量V分别为:
说明:
1)由于协方差矩阵C具有两个相同的特征值D1=D2=5,因此样本在V1和V2特征向量方向的分布是等程度的,故样本分布是一样圆形。
2)特征值D1和D2的比值越大,数据分布形状就越扁;当比值等于1时,此时样本数据分布为圆形。
协方差矩阵C的特征值D和特征向量V分别为:
说明:
1)特征值的比值D1/D2=6/4=1.5>1,因此样本数据分布形状是扁形,数据传播方向(样本的主轴方向)为V1=[0.7071 0.7071]T
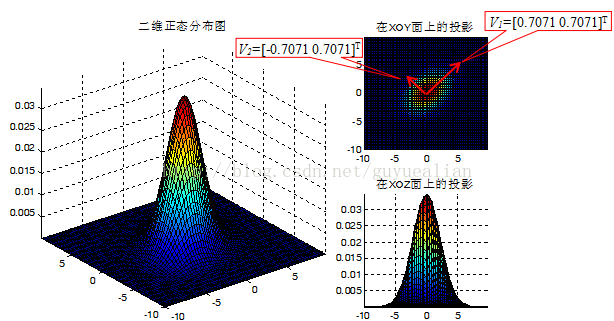
综合上述,可知:
(1)样本均值决定样本分布中心点的位置。
(2)协方差矩阵决定样本分布的扁圆程度。
是扁还是圆,由协方差矩阵的特征值决定:当特征值D1和D2的比值为1时(D1/D2=1),则样本分布形状为圆形。当特征值的比值不为1时,样本分布为扁形;
偏向方向(数据传播方向)由特征向量决定。最大特征值对应的特征向量,总是指向数据最大方差的方向(椭圆形的主轴方向)。次大特征向量总是正交于最大特征向量(椭圆形的短轴方向)。
三、协方差矩阵的应用
协方差矩阵(散布矩阵)在模式识别中应用广泛,最典型的应用是PCA主成分分析了,PCA主要用于降维,其意义就是将样本数据从高维空间投影到低维空间中,并尽可能的在低维空间中表示原始数据。这就需要找到一组最合适的投影方向,使得样本数据往低维投影后,能尽可能表征原始的数据。此时就需要样本的协方差矩阵。PCA算法就是求出这堆样本数据的协方差矩阵的特征值和特征向量,而协方差矩阵的特征向量的方向就是PCA需要投影的方向。
关于PCA的原理和分析,请见鄙人的博客:
《PCA主成分分析原理分析和Matlab实现方法》:http://blog.csdn.NET/guyuealian/article/details/68487833











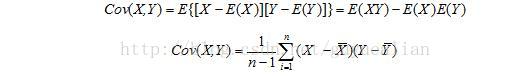
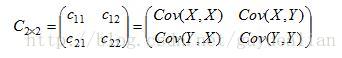
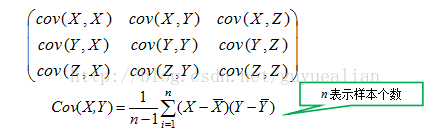


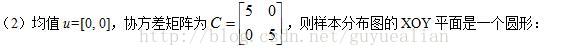

















 1889
1889

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










