C++第13周项目3——汉诺塔

课程首页地址：http://blog.csdn.net/sxhelijian/article/details/7910565

【项目3-汉诺塔】
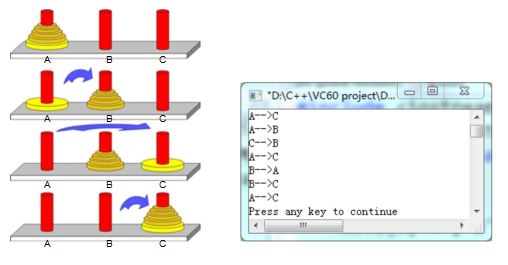
汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座，下面左图给出了移动方法的提示。请编制递归函数输出盘子数为4时（程序调试后，试试15个、20个，直至64个，看看会如何），移动的方案。下图为盘子数为3时的输出供参考。

#include <iostream>
using namespace std;
const int discCount=3;
void move(int, char, char,char);
int main()
{ 
	move(discCount,'A','B','C');
	return 0;
}


void move(int n, char A, char B,char C)
{
	if(n==1)
	{
		cout<<A<<"-->"<<C<<endl;
		return;
	}
	else
	{
		move(n-1,A,C,B);
		cout<<A<<"-->"<<C<<endl;
		move(n-1,B,A,C);
		return;
	}
}

【项目3扩展】如果要求出盘子移动的次数呢？请改写程序。
参考解答：

//仅计数
#include <iostream>
using namespace std;
const int discCount=3;
long move(int, char, char,char);
int main()
{ 
	long count;
	count=move(discCount,'A','B','C');
	cout<<discCount<<"个盘子需要移动"<<count<<"次。"<<endl;
	return 0;
}


long move(int n, char A, char B,char C)
{
	long c1,c2;
	if(n==1)
	{
		return 1;
	}
	else
	{
		c1=move(n-1,A,C,B);
		c2=move(n-1,B,A,C);
		return c1+c2+1;
	}
}

//输出且计数
#include <iostream>
using namespace std;
const int discCount=3;
long move(int, char, char,char);
int main()
{ 
	long count;
	count=move(discCount,'A','B','C');
	cout<<discCount<<"个盘子需要移动"<<count<<"次。"<<endl;
	return 0;
}


long move(int n, char A, char B,char C)
{
	long c1,c2;
	if(n==1)
	{
		cout<<A<<"-->"<<C<<endl;
		return 1;
	}
	else
	{
		c1=move(n-1,A,C,B);
		cout<<A<<"-->"<<C<<endl;
		c2=move(n-1,B,A,C);
		return c1+c2+1;
	}
}