首先,我们来了解矩阵所能做的一些特殊操作,如平移、缩放、旋转等,统称为仿射变换。其实说白了,这些特殊的效果,每一个都有一个与之对应的特殊矩阵,正是通过它们与数据矩阵进行一些运算,最后才能得到我们想要的结果。下面是常见仿射变换的构造矩阵,为了简便就先只讨论二维的吧:
1、平移
平移是最简单的一种操作,它的目的就是将一个点从当前位置转移到另一个位置。从坐标层次上来看的话,其实就是横纵坐标分别加上一个值。下面是具体的平移矩阵运算:
2、旋转
旋转是最爱考的一类操作,要实现它,我们还得借助于正弦、和余弦的威力,具体的推导这里就不详细说明了,下面直接给出结果:
3、缩放
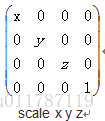
对于缩放操作的话,它有点类似于坐标层次上的平移,只是平移是加法,而缩放是乘法,下面是缩放矩阵:
3、翻转
这里定义的翻转,一般是按坐标轴进行的,如下所示:
有了上面的这些特殊矩阵,我们就可以优化一些运算,比如当对n个点做m次变换时,如果直接模拟,那时间复杂度就是O(n*m),但是使用上面的矩阵在O(m)的时间内将所有操作合并在一个矩阵里,然后再在O(n)的时间内对每一个点实施变换的话,总时间复杂度将减少至O(n+m)。光说不练不行,下面就利用一道题进行实际的操作,HDOJ:4087,时空转移(点击打开链接),题目如下:
ALetter to Programmers
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 858 Accepted Submission(s): 274
I can imagine how surprised you are when you receive this strange letter. Well, be patient, I am going to talk about some really exciting things that you must be interested in.
First of all, I have to congratulate everyone of you - the gifted programmers, for you are so lucky to have a God-given chance to be my inheritor - a new Deity of Stars. However, you know that it is difficult for an ordinary person to become a deity, so only the best one among you can finally be chosen. Therefore, you are facing a hard test for estimating your abilities.
Try your best to compete!
The Deity of Stars, of course, is the unique dominator of all stars in the whole universe, which means controlling the stars' tracks and ensuring that the stars move in their own orbit are his/her most important responsibilities. What? You will be sick in managing incalculable stars? Don't worry, it will be a piece of cake once you have a wonderful tool - a special kind of programming language. That is why I am going to choose my inheritor from you.
So in your test, you will be given a special program and the initial positions of some stars (In deities' eyes, the stars are so small that they can be regarded as points), you need to figure out the new positions of these stars after the program is executed.
Considering all of you are green hands, I will just give you a program in a simple
version during the test, which contains only several kinds of instructions listed below:
1. translate tx ty tz
Everything in (x, y, z) must be moved to ( x+tx, y+ty, z+tz)
2. scale a b c
Everything in (x, y, z) will be moved to (ax, by, cz)
3. rotate a b c d
It will make everything rotate. The rotation axis is the straight line from (0, 0, 0) to (a, b, c), and the angle of rotation is d (measured in degrees). If you stand at (a, b, c) and look at (0, 0, 0),you will see that the rotation is counterclockwise.
4. repeat k
The instructions between a "repeat" instruction and an "end" instruction matched with it (will be explained later) will be executed for k times. The integer k is non-negative and a 32-bit signed integer is sufficient to deal with it.
5. end
If there are some unmatched "repeat" instructions, the "end" instruction will be matched with the nearest unmatched "repeat" instruction before it; otherwise, it indicates the end of the program. Please note that a repeat-end pair may include other repeat-end pairs.
Now the test is coming. Are you ready?
Good Luck,
Zi Wei, Emperor of North Polaris
Each test case begins with one integer n (1 <= n <= 1000), indicating the number of the given points. Then there is a correct program without any extra blanks or redundant characters and it contains less than 100 lines. Each line contains only one instruction. Then n lines follow, each containing three numbers which indicate the coordinates of a po int in 3D universe. All numbers except n and k are floats and no more than 1000 in absolute value.
Two consecutive cases are separated by a blank line.
The input ends with n = 0.
Print a blank line after each test case.
2 rotate 1.0 1.0 1.0 90.0 translate 2.0 2.0 2.0 end 1.0 1.0 1.0 1.0 0.0 0.0 3 repeat 100 translate 2.7 -0.2 1.1 translate -2.6 0.0 -1.0 end scale 1.0 0.0 0.5 end 0.5 2.7 1.1 0.22 0 7.0 1.2 3.4 5.6 0
3.00 3.00 3.00 2.33 2.91 1.76 10.50 0.00 5.55 10.22 0.00 8.50 11.20 0.00 7.80
题意:
大概意思就是对给出的点进行仿射变换,平移、缩放、旋转,最后输出变换后点的坐标。
分析:
这道题需要注意三个问题,一是三维坐标,二是旋转是绕任意轴(过原点)旋转,三是时间问题。第一个问题好解决,在前面我们得出的仿射矩阵上增加维数即可,如下所示:

要解决第二个问题的话,估计还是要有两把刷子的大牛才能推导出来的,我这里就借用结论了:
对于第三个问题,运算中出现的最为费时的幂次,我们同样使用经典的快速幂算法优化计算速度。对了,还有最后一点,这道题目的输入也是坑爹的,看了大家的做法,发现只有利用递归的思想去处理输入是比较好的。
源代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define LL __int64
using namespace std;
const int MAXN = 5;
const int MOD = 1e5;
const double eps = 1e-6;
const double pi = acos(-1.0);
struct Mat
{
int n, m;
double mat[MAXN][MAXN];
Mat()
{
memset(mat, 0, sizeof(mat));
n = m = MAXN-1;
};
void init() // 初始化为单位矩阵
{
for(int i=1; i<=n; ++i)
for(int j=1; j<=m; ++j)
mat[i][j] = (i==j);
}
Mat operator * (Mat b) // 重载乘法
{
Mat c;
c = Mat();
c.n = n;
c.m = b.m;
for(int i=1; i<=n; ++i) // 注意这里从1开始
for(int j=1; j<=b.m; ++j)
{
//if(mat[j][i] <= 0) continue; // 剪枝
for(int k=1; k<=m; ++k)
{
//if(b.mat[i][k] <= 0) continue; // 剪枝
c.mat[i][j] += (mat[i][k]*b.mat[k][j]); //% MOD;
//c.mat[i][j] %= MOD;
}
}
return c;
}
Mat operator + (Mat b) // 重载加法
{
Mat c;
c.n = n;
c.m = m;
for(int i=1; i<=n; ++i)
for(int j=1; j<=m; ++j)
c.mat[i][j] = (mat[i][j]+b.mat[i][j]); //% MOD;
return c;
}
Mat QuickPow(Mat a, int k) // 快速幂
{
Mat c;
c.n = a.n;
c.m = a.n;
c.init(); // 初始化为单位矩阵
while(k)
{
if(k & 1)
c = c*a;
a = a*a;
k >>= 1;
}
return c;
}
void translate(Mat &a, double x, double y, double z) // 平移(三维)
{
Mat c;
c.init();
c.mat[1][4] = x;
c.mat[2][4] = y;
c.mat[3][4] = z;
a = c * a;
}
void scale(Mat &a, double x, double y, double z) // 缩放(三维)
{
Mat c;
c.init();
c.mat[1][1] = x;
c.mat[2][2] = y;
c.mat[3][3] = z;
a = c * a;
}
void rotat(Mat &a, double x, double y, double z, double d) // 旋转(三维),以(0,0,0),(x,y,z)线段为旋转轴,旋转d度
{
d = d/180 * pi;
double di = sqrt(x*x+y*y+z*z); // 单位化
x/=di, y/=di, z/=di;
Mat c;
c.init();
c.mat[1][1] = (1-cos(d))*x*x + cos(d);
c.mat[1][2] = (1-cos(d))*x*y - z*sin(d);
c.mat[1][3] = (1-cos(d))*x*z + y*sin(d);
c.mat[2][1] = (1-cos(d))*x*y + z*sin(d);
c.mat[2][2] = (1-cos(d))*y*y + cos(d);
c.mat[2][3] = (1-cos(d))*y*z - x*sin(d);
c.mat[3][1] = (1-cos(d))*x*z - y*sin(d);
c.mat[3][2] = (1-cos(d))*y*z + x*sin(d);
c.mat[3][3] = (1-cos(d))*z*z + cos(d);
a = c * a;
}
};
Mat DfsI(int n) // 递归输入
{
Mat tmp;
tmp.init();
char s[100];
while(~scanf("%s", s))
{
if(s[0] == 't')
{
double x, y, z;
scanf("%lf%lf%lf", &x,&y,&z);
tmp.translate(tmp, x, y, z);
continue;
}
if(s[0] == 's')
{
double x, y, z;
scanf("%lf%lf%lf", &x, &y, &z);
tmp.scale(tmp, x, y, z);
continue;
}
if(s[0]=='r' && s[1]=='o')
{
double x, y, z, d;
scanf("%lf%lf%lf%lf", &x, &y, &z, &d);
tmp.rotat(tmp, x, y, z, d);
continue;
}
if(s[0]=='r' && s[1]=='e')
{
int n;
scanf("%d", &n);
tmp = DfsI(n) * tmp;
}
if(s[0] == 'e')
{
tmp = tmp.QuickPow(tmp, n);
return tmp;
}
}
}
int main()
{//freopen("sample.txt", "r", stdin);
int n;
while(~scanf("%d", &n) && n)
{
Mat data;
data.init();
data = DfsI(1) * data; // 递归输入数据并处理出最终的仿射变换矩阵
Mat p; // 输入的点
p.n = 4;
p.m = 1;
for(int i=0; i<n; ++i)
{
for(int i=1; i<=3; ++i)
scanf("%lf", &p.mat[i][1]);
p.mat[4][1] = 1;
p = data * p; // 变换矩阵乘上初始点矩阵得出变换后的点矩阵
printf("%.2f %.2f %.2f\n",
p.mat[1][1]+eps, p.mat[2][1]+eps, p.mat[3][1]+eps); // 注意 -0.00 !,需要修正
}
puts("");
}
return 0;
}
好了,由于时间问题,有关矩阵的讨论就说到这里了,其实还有许多有趣的用法,如螺旋变换等,另外还有一些未涉足的知识,如矩阵在离散数学中的应用(HDU2157),在图论中的应用,算了,只有后面再补充喽。最后,下面打一份矩阵 的模版,其实还可以扩展,以此作为结束吧:
#define LL __int64
using namespace std;
const int MAXN = 5; // 矩阵的最大行和列
const int MOD = 1e5; // 如果可以不用取模,则尽量不用
const double eps = 1e-6; // 处理细小的精度问题
const double pi = acos(-1.0); // 圆周率
struct Mat
{
int n, m;
double mat[MAXN][MAXN];
Mat()
{
memset(mat, 0, sizeof(mat));
n = m = MAXN-1;
};
void init() // 初始化为单位矩阵
{
for(int i=1; i<=n; ++i)
for(int j=1; j<=m; ++j)
mat[i][j] = (i==j);
}
Mat operator * (Mat b) // 重载乘法
{
Mat c;
c = Mat();
c.n = n;
c.m = b.m;
for(int i=1; i<=n; ++i) // 注意这里从1开始
for(int j=1; j<=b.m; ++j)
{
//if(mat[j][i] <= 0) continue; // 剪枝
for(int k=1; k<=m; ++k)
{
//if(b.mat[i][k] <= 0) continue; // 剪枝
c.mat[i][j] += (mat[i][k]*b.mat[k][j]) % MOD;
c.mat[i][j] %= MOD;
}
}
return c;
}
Mat operator + (Mat b) // 重载加法
{
Mat c;
c.n = n;
c.m = m;
for(int i=1; i<=n; ++i)
for(int j=1; j<=m; ++j)
c.mat[i][j] = (mat[i][j]+b.mat[i][j]) % MOD;
return c;
}
Mat QuickPow(Mat a, int k) // 快速幂
{
Mat c;
c.n = a.n;
c.m = a.n;
c.init(); // 初始化为单位矩阵
while(k)
{
if(k & 1)
c = c*a;
a = a*a;
k >>= 1;
}
return c;
}
Mat transpose() // 求矩阵的转置
{
Mat c;
c.n = m;
c.m = n;
for(int i=1; i<=n; ++i)
for(int j=1; j<=m; ++j)
c.mat[j][i] = mat[i][j];
/*for(int i=1,j=m; i<j; ++i,--j) // 如果加上这里的代码的话,就是矩阵旋转本身
for(int k=1; k<=n; ++k)
{
int tmp = c.mat[k][i];
c.mat[k][i] = c.mat[k][j];
c.mat[k][j] = tmp;
}*/
return c;
}
Mat slove(Mat init, int k) // 递归二分求解递增幂次和
{
if(k == 1)
return init;
Mat c;
c.n = init.n;
c.m = init.m;
c = slove(init, k>>1);
c = c + c * init.QuickPow(init,k>>1);
if(k & 1)
return c + init.QuickPow(init,k);
else
return c;
}
void translate(Mat &a, double x, double y, double z) // 平移(三维)
{
Mat c;
c.init();
c.mat[1][4] = x;
c.mat[2][4] = y;
c.mat[3][4] = z;
a = c * a;
}
void scale(Mat &a, double x, double y, double z) // 缩放(三维)
{
Mat c;
c.init();
c.mat[1][1] = x;
c.mat[2][2] = y;
c.mat[3][3] = z;
a = c * a;
}
void rotat(Mat &a, double x, double y, double z, double d) // 旋转(三维),以(0,0,0),(x,y,z)线段为旋转轴,旋转d度
{
d = d/180 * pi;
double di = sqrt(x*x+y*y+z*z); // 单位化
x/=di, y/=di, z/=di;
Mat c;
c.init();
c.mat[1][1] = (1-cos(d))*x*x + cos(d);
c.mat[1][2] = (1-cos(d))*x*y - z*sin(d);
c.mat[1][3] = (1-cos(d))*x*z + y*sin(d);
c.mat[2][1] = (1-cos(d))*x*y + z*sin(d);
c.mat[2][2] = (1-cos(d))*y*y + cos(d);
c.mat[2][3] = (1-cos(d))*y*z - x*sin(d);
c.mat[3][1] = (1-cos(d))*x*z - y*sin(d);
c.mat[3][2] = (1-cos(d))*y*z + x*sin(d);
c.mat[3][3] = (1-cos(d))*z*z + cos(d);
a = c * a;
}
void in(int x, int y) // 输入矩阵
{
n = x;
m = y;
for(int i=1; i<=n; ++i)
for(int j=1; j<=m; ++j)
{
scanf("%lf", &mat[i][j]);
mat[i][j] %= MOD;
}
}
void out() // 输出矩阵
{
for(int i=1; i<=n; ++i)
{
printf("%f", mat[i][1]);
for(int j=2; j<=m; ++j)
printf(" %f", mat[i][j]);
puts("");
}
}
};







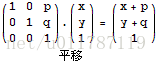

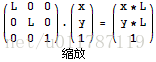


















 2325
2325

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








