限制玻尔兹曼机（RBMs）理论详解

一、序

关于RBMs的文章已经有不少了，但是很多资料我在阅读的时候仍然对细节有一些疑惑。在查阅学习了大牛的视频、论文之后，很多问题豁然开朗，且在本文中记录下我对RBMs的粗浅了解。首先从玻尔兹曼机和限制玻尔兹曼机的结构和定义开始：

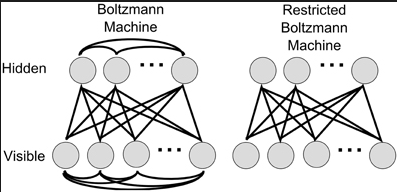
二、Boltmann Machines：

    玻尔兹曼机（Boltmann Machines）的能量函数（Energy function）是：

$$\begin{equation} E(\textbf{x}, \textbf{h}) = -\textbf{h}^\top \textbf{W} \textbf{x} - \textbf{c}^\top \textbf{x} - \textbf{b}^\top \textbf{h} - \textbf{x}^\top \textbf{U} \textbf{x} - \textbf{h}^\top \textbf{V} \textbf{h} \end{equation}$$

分布函数：

$$\begin{equation} P(\textbf{x}, \textbf{h}) = exp(-E(\textbf{x}, \textbf{h}))/Z \end{equation}$$

其中分母Z学名叫做partition function

$$\begin{equation} Z = \sum_{\textbf{x}} \sum_{\textbf{h}} exp(-E(\textbf{x}, \textbf{h})) \end{equation}$$

三、Restricted Boltmann Machines：

    限制玻尔兹曼机（Restricted Boltmann Machines，简称RBMs）的能量函数（Energy function）是：

$$\begin{equation} \begin{split} &E(\textbf{x}, \textbf{h}) = -\textbf{h}^\top \textbf{W} \textbf{x} - \textbf{c}^\top \textbf{x} - \textbf{b}^\top \textbf{h}\\ &\;\;=-\sum_j \sum_k W_{j,k}h_j x_k - \sum_k c_k x_k - \sum_j b_j h_j\\ \end{split} \end{equation}$$

分布函数：

$$\begin{equation} P(\textbf{x}, \textbf{h}) = \exp(-E(\textbf{x}, \textbf{h}))/Z \end{equation}$$
能量函数的能量越小，分布函数相应的概率就越大。

      玻尔兹曼机和限制玻尔兹曼机都属于基于能量的模型（Energy-Based Models），从模型图和公式中很容易看出两者的区别：玻尔兹曼机隐含层（和可见层）处于同一层的任意两个节点之间有一条连线；而限制玻尔兹曼机同层变量之间是相互独立的。只要有足够的隐单元，限制玻尔兹曼机可以表示任意的离散分布，玻尔兹曼机的表示能力则更强一些。另一方面，限制玻尔兹曼机比玻尔兹曼机更容易训练。

四、模型学习：

    训练RBMs就是学习能量函数的过程，变量中只有输入$\textbf{x}$是已知的。

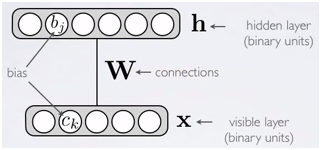
Free Energy：

    为了后面计算公式的简洁，首先引入Free Energy这个概念：

$$\begin{equation} P(\textbf{x}) = \sum_{\textbf{h}} \frac{e^{-E(\textbf{x}, \textbf{h})}}{Z} = \frac{e^{-FreeEnergy(\textbf{x})}}{Z},\;\; Z = \sum_{\textbf{x}}e^{-FreeEnergy(\textbf{x})} \end{equation}$$

$$\begin{equation} FreeEnergy(\textbf{x}) = -log \sum_{\textbf{h}} e^{-E(\textbf{x}, \textbf{h})} \end{equation}$$

例如：如果$h_i\in \{0,1\}$：

$$\begin{equation} \begin{split} &FreeEnergy(\textbf{x}) = -log \sum_{\textbf{h}} e^{-E(\textbf{x}, \textbf{h})}=-log \sum_{\textbf{h}} e^{\textbf{h}^\top \textbf{W} \textbf{x} + \textbf{c}^\top \textbf{x} + \textbf{b}^\top \textbf{h}}\\ &=-\textbf{c}^\top \textbf{x}-log \sum_{\textbf{h}} e^{\textbf{h}^\top \textbf{W} \textbf{x} + \textbf{b}^\top \textbf{h}} = -\textbf{c}^\top \textbf{x}-log \sum_{\textbf{h}} e^{h_1( \textbf{W}_{1\cdot} \textbf{x} + b_1)}\cdots e^{h_n( \textbf{W}_{n\cdot} \textbf{x} + b_n)}\\ &=-\textbf{c}^\top \textbf{x}- \sum_{i} log (1+e^{ \textbf{W}_{i\cdot} \textbf{x} + b_i})\\ \end{split} \end{equation}$$
给定参数和 $\textbf{x}$就可以很容易的计算出Free Energy的值，不依赖于隐单元 $\textbf{h}$的具体取值。

梯度方法进行优化：

      用梯度算法学习RBMs模型参数$\theta$($\theta$包括$\textbf{W},\textbf{c},\textbf{b}$)，目标函数是$P(\textbf{x})$（这里是梯度上升，因为要求的是似然的极大值）。$P(\textbf{x})$取对数求偏导：

$$\begin{equation} log P(\textbf{x}) = -FreeEnergy(\textbf{x}) - log Z \end{equation}$$
对数似然梯度（log-likelihood gradient）：
$$\begin{equation} \begin{split} &\frac{\partial log P(\textbf{x})}{\partial \theta} = - \frac{\partial FreeEnergy(\textbf{x})}{\partial \theta} + \frac{1}{Z} \sum_{\tilde{\textbf{x}}} e^{-FreeEnergy(\tilde{\textbf{x}})} \frac{\partial FreeEnergy(\tilde{\textbf{x}})}{\partial \theta}\\ &\;\;\;\;= - \frac{\partial FreeEnergy(\textbf{x})}{\partial \theta} + \sum_{\tilde{\textbf{x}}} P(\tilde{\textbf{x}}) \frac{\partial FreeEnergy(\tilde{\textbf{x}})}{\partial \theta}\\ \end{split} \end{equation}$$
$\frac{\partial log P(\textbf{x})}{\partial \theta}$ 是对 $\frac{\partial log P(\textbf{x})}{\partial \textbf{W}}, \frac{\partial log P(\textbf{x})}{\partial \textbf{c}}, \frac{\partial log P(\textbf{x})}{\partial \textbf{b}}$ 的统一表示，编写代码时需要分别求偏导。求偏导都没有太大难度，其中 $\frac{\partial E(\textbf{x}, \textbf{h})}{\partial \textbf{W}} = \frac{\partial -\textbf{h}^\top \textbf{W} \textbf{x}}{\partial \textbf{W}} = -\textbf{h}\textbf{x}^\top$。

        很多文章里喜欢写成负对数似然梯度（negative log-likelihood gradient）的形式，$-log P(\textbf{x})$就应该用梯度下降方法来更新参数了：

$$\begin{equation} - \frac{\partial log P(\textbf{x})}{\partial \theta} = \frac{\partial FreeEnergy(\textbf{x})}{\partial \theta} - \sum_{\tilde{\textbf{x}}} P(\tilde{\textbf{x}}) \frac{\partial FreeEnergy(\tilde{\textbf{x}})}{\partial \theta} \end{equation}$$

训练集上的平均负对数似然梯度等于：

$$\begin{equation} E_{\hat{P}}[\frac{\partial -log P(\textbf{x})}{\partial \theta}] = E_{\hat{P}}[\frac{\partial FreeEnergy(\textbf{x})}{\partial \theta}] - E_P[\frac{\partial FreeEnergy(\tilde{\textbf{x}})}{\partial \theta}] \end{equation}$$
$\hat{P}$是训练集对应的分布， $P$是模型分布，$E_P$表示在模型分布上求期望。（这里顺便解释一下为什么大家都喜欢负对数似然而不是直接最大化似然，其实如果你有一台可以表示任何数值的超级计算机，那么取不取对数真的没什么关系，但是现实中的计算机表示能力有限，N个训练样本似然乘积很小很小，小到计算机都无法表示了，所以最好取log，概率的和不会有这样的问题；另外，在优化理论中，优化问题的标准形式就是最小化某个目标函数，所以最好加个负号，最小化负对数似然）。

    式子的第一项称为positive phrase，通过减小对应的FreeEnergy增大训练样本的概率；第二项是negative phrase，作用是增大对应的FreeEnergy来减小模型产生的样本的概率。句话不难理解，因为两项分别是往$FreeEnergy(\textbf{x})$的梯度下降和$FreeEnergy(\tilde{\textbf{x}})$的梯度上升方向改变。这也符合最大似然标准，在训练样本上有较大的似然而在其他样本上概率较小。从分类的角度来看，训练样本是正样本，而模型样本是负样本(Negative samples)。

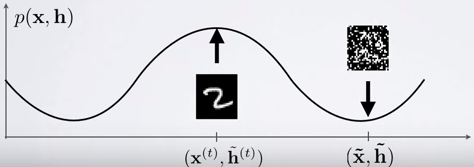
    把训练样本代入求均值即可得到梯度公式的第一项$E_{\hat{P}}[\frac{\partial FreeEnergy(\textbf{x})}{\partial \theta}]$的值，第二项$E_P[\frac{\partial FreeEnergy(\tilde{\textbf{x}})}{\partial \theta}]$计算模型分布上的期望，这就比较困难了，因为这需要取遍所有可能的$\textbf{x}$的值。所以接下来我们就需要用到MCMC 采样来近似估计了。用MCMC采样得到的一组样本来近似估计整体的样本分布，梯度公式第二项在采样得到的样本上求近似期望（平均值）得到估计值。在实际中，常用Gibbs采样，Gibbs 采样是MCMC 算法的一种。用Gibbs从模型分布中采样n个样本，然后负对数似然梯度在训练集上的期望就可以近似为：

$$\begin{equation} E_{\hat{P}}[\frac{\partial -log P(\textbf{x})}{\partial \theta}] \approx E_{\hat{P}}[\frac{\partial FreeEnergy(\textbf{x})}{\partial \theta}] - \frac{1}{n}\sum_{i=1}^n\frac{\partial FreeEnergy(\tilde{\textbf{x}_i})}{\partial \theta} \end{equation}$$

        最后，简要概括一下RBMs模型学习方法的步骤：（1）、求偏导，（2）、采样，（3）、估计负对数似然梯度，（4）、梯度下降方法更新参数。

五、Gibbs采样：

      对RBMs模型来说， Gibbs主要有两个作用：一是估计negative log-likelihood gradient；二是在训练完模型之后（如DBN，DBN是由多个RBMs叠加而成的），用Gibbs进行采样，可以看到模型对数据的拟合以及网络中间隐含层的抽象效果。

       在RBMs模型训练过程中，Gibbs就是用来对negative log-likelihood gradient进行估计的。Gibbs采样分两个小步对$(\textbf{x}, \textbf{h})$进行采样，第一步固定$\textbf{x}$对$\textbf{h}$进行采样，第二步固定$\textbf{h}$对$\textbf{x}$进行采样，交替进行直到收敛：

$$\begin{equation} \begin{split} &\textbf{x}_1 \sim \hat{P}(x)\\ &\textbf{h}_1 \sim P(\textbf{h}|\textbf{x}_1)\\ &\textbf{x}_2 \sim P(\textbf{x}|\textbf{h}_1)\\ &\textbf{h}_2 \sim P(\textbf{h}|\textbf{x}_2)\\ &\;\;\;\;\;\;\;\;\;\;\vdots \\ &\textbf{x}_{k+1} \sim P(\textbf{x}|\textbf{h}_k)\\ \end{split} \end{equation}$$
    因为在训练过程中，训练模型分布会逐渐逼近训练样本分布，所以第一步可以从训练样本的分布 $\hat{P}$抽取样本作为 $\textbf{x}_1$。如果第一步直接从模型 $P$ 中采样，Gibbs采样会迅速收敛。

    例如:假设$\textbf{h} \in \{0,1\}^H$,已经得到 $\textbf{x}_1$，需要对 $\textbf{h}_1$采样。 $P(\textbf{h}| \textbf{x}) = \prod_{j}p(h_j|\textbf{x})$（注：条件分布的具体推导过程见下一小节内容）， 由于隐单元之间是相互独立的，所以可以采用block Gibbs采样，对所有的隐单元同时进行采样，加快采样收敛。分别求 $p(h_j=1|\textbf{x})$，如果 $p(h_j=1|\textbf{x})\ge U[0,1]$（大于等于均匀分布的一个采样），就设置 $h_j = 1$，否则设置 $h_j = 0$。

条件分布：

    Gibbs采样主要是根据条件分布迭代进行采样的，所以在采样之前要先推导出条件分布公式。

$$\begin{equation} \begin{split} &P(\textbf{h}| \textbf{x}) = P(\textbf{x}, \textbf{h})/\sum_{\textbf{h}'} P(\textbf{x}, \textbf{h}')\\ &\;\;=\frac{exp(\textbf{h}^\top \textbf{W} \textbf{x} + \textbf{c}^\top \textbf{x} + \textbf{b}^\top \textbf{h})/Z}{\sum_{\textbf{h}'} exp(\textbf{h}'^\top \textbf{W} \textbf{x} + \textbf{c}^\top \textbf{x} + \textbf{b}^\top \textbf{h}')/Z}\\ &\;\;=\frac{exp(\textbf{h}^\top \textbf{W} \textbf{x} + \textbf{b}^\top \textbf{h})}{\sum_{\textbf{h}'} exp(\textbf{h}'^\top \textbf{W} \textbf{x} + \textbf{b}^\top \textbf{h}')} \;\;\text{分子分母同时约去h无关项}\\ &\;\;=\frac{exp(\sum_{{h}_j}{h}_j W_{j\cdot} \textbf{x} + b_j {h}_j)}{\sum_{\textbf{h}'} exp(\sum_{{h'}_j}{h'}_j W_{j\cdot} \textbf{x} + b_j {h'}_j)} \;\;W_{j\cdot}\text{是W的第j行}\\ &\;\;=\frac{\prod_{j} exp({h}_j W_{j\cdot} \textbf{x} + b_j {h}_j)}{\sum_{{h'}_1}...\sum_{{h'}_H} \prod_{j} exp({h'}_j W_{j\cdot} \textbf{x} + b_j {h'}_j)} \\ &\;\;=\frac{\prod_{j} exp({h}_j W_{j\cdot} \textbf{x} + b_j {h}_j)}{\prod_{j} \sum_{{h'}_j} exp({h'}_j W_{j\cdot} \textbf{x} + b_j {h'}_j)} \\ &\;\;= \prod_{j} \frac{ exp({h}_j W_{j\cdot} \textbf{x} + b_j {h}_j)}{ \sum_{{h'}_j} exp({h'}_j W_{j\cdot} \textbf{x} + b_j {h'}_j)} \\ &\;\;= \prod_{j}p(h_j|\textbf{x})\\ \end{split} \end{equation}$$

如果$h_j \in \{0,1\}$，可以得到：

$$\begin{equation} p(h_j = 1|\textbf{x}) = \frac{ exp( W_{j\cdot} \textbf{x} + b_j )}{ 1 + exp( W_{j\cdot} \textbf{x} + b_j)} = sigm(W_{j\cdot} \textbf{x} + b_j) \end{equation}$$

$$\begin{equation} p(h_j = 0|\textbf{x}) = 1 - p(h_j = 1|\textbf{x}) \end{equation}$$

类似的：

$$\begin{equation} P(\textbf{x}| \textbf{h}) = \prod_{j} \frac{ exp(\textbf{h} W_{\cdot j} x_j + c_j x_j)}{ \sum_{{x'}_j} exp(\textbf{h} W_{\cdot j} {x'}_j + c_j {x'}_j))} = \prod_{j}p(x_j|\textbf{h}) \end{equation}$$

如果$x_j \in \{0,1\}$，可以得到：

$$\begin{equation} p(x_j = 1| \textbf{h}) = \frac{ exp(\textbf{h} W_{\cdot j} + c_j )}{ 1 + exp(\textbf{h} W_{\cdot j} + c_j))} = sigm(\textbf{h} W_{\cdot j} + c_j) \end{equation}$$

六、Contrastive Divergence:

    Contrastive Divergence可以加快RBMs的训练速度，随机选择一个训练样本初始化$\textbf{x}_1$，并且每一次迭代只用一个模型样本来估计negative log-likelihood gradient，而不是等到MCMC采样收敛后求期望。

    k-step Contrastive Divergence（CD-k）：MCMC采样k步$\textbf{x}_1,\textbf{x}_2,...,\textbf{x}_{k+1}$， 用 $\textbf{x}_{k+1}$ 估计negative log-likelihood gradient。当k=1时，就能得到比较好的近似（DBN等pre-training k取1就够用了），k增大可以得到更好的效果。Contrastive Divergence的一种理解是在训练样本$\textbf{x}_1$ 附近的局部区域内估计negative log-likelihood gradient。

借用一下大神Bengio的文章”Learning Deep Architectures for AI”的算法描述：

Persistent CD:

    CD只在附近的局部区域取Negative Sample来估计negative log-likelihood gradient，很难取到其它极值区域的样本，Persistent CD可以在一定程度上解决这个问题。Persistent CD的思想很简单，它与CD的区别仅仅在与：用上一次迭代得到的 $\textbf{x}_{k+1}$（即Negative Sample）作为这次迭代的初始值来初始化$\textbf{x}_1$。PS：Persistent CD是2008年Tijmen发表在ICML上的文章。

七、参考资料：

[1].Youtube上Hugo Larochelle的视频讲解：https://www.youtube.com/user/hugolarochelle/videos

[2].DeepLearning tutorial：http://deeplearning.net/tutorial/rbm.html

[3].LSIA：http://www.iro.umontreal.ca/~lisa/twiki/bin/view.cgi/Public/DBNEquations

[4].Yoshua Bengio：Learning Deep Architectures for AI