【Wilcoxon 检验】威尔科克森秩检验[非参数检验](Matlab代码实现）

最新推荐文章于 2025-04-30 14:27:27 发布

程序辅导帮

最新推荐文章于 2025-04-30 14:27:27 发布

阅读量751

点赞数 20

文章标签： matlab 机器学习算法

本文链接：https://blog.csdn.net/2201_75454341/article/details/147601696

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

威尔科克森检验（Wilcoxon Test）详解

一、基本定义与类型

二、假设条件

（一）秩和检验（独立样本）的假设

（二）符号秩检验（配对样本/单样本）的假设

三、计算步骤

（一）秩和检验（独立样本）

（二）符号秩检验（配对样本）

四、应用场景案例

（一）秩和检验案例

（二）符号秩检验案例

五、优缺点分析

优点：

缺点：

六、注意事项与扩展

七、总结

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

威尔科克森检验（Wilcoxon Test）详解

假设数据是关于坐标原点对称，那么对称中心两侧的数据疏密程度应一致，取正值数据在绝对值样本中的秩和与取负值在绝对值样本中的秩和相近。

一、基本定义与类型

威尔科克森检验是一类非参数统计方法的统称，主要包括两种类型：

秩和检验（Wilcoxon Rank-Sum Test） ：用于比较两个独立样本的中位数差异，等效于曼-惠特尼U检验。
符号秩检验（Wilcoxon Signed-Rank Test） ：用于配对样本或单样本的中位数检验，替代配对t检验。

两者的核心特点是不依赖总体分布的正态性假设，通过数据排序（秩次）构建统计量，适用于以下场景：

数据为序数、离散或非正态分布；
样本量小（如n<30）；
存在异常值或测量尺度不满足参数检验要求。

二、假设条件

（一）秩和检验（独立样本）的假设

样本独立且随机抽取；
变量为连续型（理论上可无限细分）；
两组数据的分布形状相同（仅位置参数不同）。

（二）符号秩检验（配对样本/单样本）的假设

配对观测值独立且来自同一总体；
差异服从对称分布（单样本需总体对称）；
测量尺度至少为区间尺度（如温度、时间）。

注：若差异不对称或存在大量零差异，需使用改进方法（如普拉特修正）。

三、计算步骤

（一）秩和检验（独立样本）

合并排序：将两组数据合并，按升序排列并分配秩次（如遇相同值取平均秩）；
计算秩和：分别求两组的秩和R1R1和R2R2；
构建统计量：使用U=min⁡(U1,U2)，其中Ui=n1n2+ni(ni+1)2−Ri；
推断结论：查U分布表或大样本时用正态近似Z=U−μUσUZ=σUU−μU计算p值。

公式示例：

（二）符号秩检验（配对样本）

计算差异：每对观测值差di=xi−yi，排除零差异；
排序绝对值：按∣di∣升序分配秩次，相同值取平均秩；
符号分配：根据di符号赋予秩次正负号；
统计量选择：取正秩和W+或负秩和W−中的较小值；
假设检验：查W分布表或大样本时用正态近似。

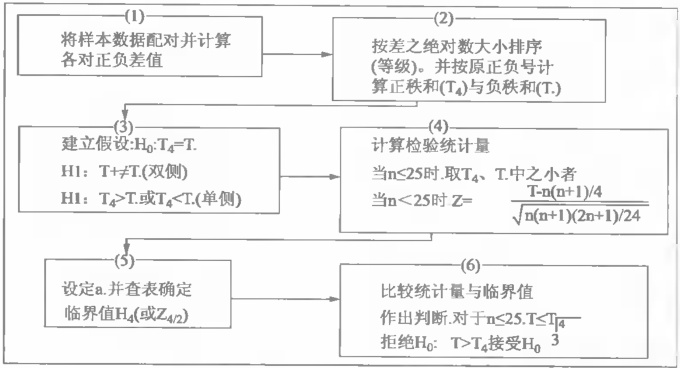
大样本校正公式：

（其中tj为结的数量）。

四、应用场景案例

（一）秩和检验案例

工业检测：比较两台机器生产的零件直径是否相同（数据非正态）。
医学研究：分析两种药物对血压的影响（独立患者组）。

（二）符号秩检验案例

临床试验：评估保健品对小鼠抗疲劳效果（配对设计，游泳时间差异非正态）。
质量控制：检测罐装食品重量是否符合标准100g（单样本，数据右偏）。

五、优缺点分析

优点：

稳健性：不依赖正态假设，对异常值不敏感；
适用性广：支持序数、离散和连续数据；
小样本有效：即使n<30也能提供可靠结果。

缺点：

效力较低：若数据满足参数条件，检验效力弱于t检验；
信息损失：仅利用秩次，忽略具体数值差异；
结的处理复杂：相同值影响方差计算，需校正。

六、注意事项与扩展

效应量计算：推荐使用Cliff's delta或秩二列相关系数（R语言effectsize包）。
软件实现：
- R语言：wilcox.test(x, y, paired=FALSE)（秩和检验）；
- Python：scipy.stats.wilcoxon()（符号秩检验）。
与Mann-Whitney U检验的关系：秩和检验与U检验数学等价，但统计量计算方式不同。

七、总结

威尔科克森检验为非参数统计的核心工具，特别适用于非正态数据和小样本场景。研究者在选择时需明确数据类型（独立/配对）、检验假设及实际需求，结合效应量和稳健性分析，以提升结论的科学性。

📚2 运行结果

部分代码：

function [dist, w] = wilcoxon_dist_groups(pH0, Neq0, T, strateq0)

N = Neq0 + sum(T);
w = (0:0.5:(N*(N+1)/2)); % range of possible values
dist = zeros(size(w));

ranks = Neq0+cumsum(T)-0.5*(T-1); % ranks for non-zero groups

% handle 0's
if Neq0 > 0
switch strateq0
case 'Wilcoxon'
% after Wilcoxon 1945 "Individual Comparisons by Ranking
% Methods":
% discard 0's and adjust remaining ranks by subtracting Neq0
%
% adjust the ranks
ranks = ranks - Neq0;
% The ranksum resulting from the Neq 0's is R = 0
dist(1) = 1;
case 'Pratt'
% after Pratt 1959 "Remarks on Zeros and Ties in the Wilcoxon
% Signed Rank Procedures":
% discard 0's and without adjusting the remaining ranks.

% The ranksum resulting from the Neq 0's is R = 0
dist(1) = 1;
case 'Marascuilo'
% after Marascuilo 1977 "Nonparametric and Distribution-free
% Methods for the Social Sciences":
% shared rank of the 0's is accounted by one half to the ranksum
%
% The first Neq0 values share the rank (1 + 2 + ... + Neq0)/ Neq0
% = (Neq0+1)/2. Their ranksum is R = Neq*(Neq0+1)/4
Req0 = Neq0*(Neq0+1)/4;
dist(2*Req0+1) = 1;
end
else
dist(1) = 1;
end

% handle remaining ranks for non-zero values
for rdx=1:length(T)
shift = 2*ranks(rdx);
for tdx=1:T(rdx)
dist = pH0*dist + (1-pH0).*[zeros(1,shift),dist(1:end-shift)];
end
end