Logistic回归（第五章）

最新推荐文章于 2024-07-13 21:34:41 发布

向日葵Aurora

最新推荐文章于 2024-07-13 21:34:41 发布

阅读量840

点赞数 20

文章标签：回归人工智能深度学习机器学习自然语言处理

本文链接：https://blog.csdn.net/2301_79861957/article/details/136993634

版权

Logistic回归（第五章）

文章目录

Logistic回归（第五章）
一、线性回归简介
二、 Logistic回归简介
三、用PyTorch实现Logistic
笔记
1.反向传播
2.逻辑回归与线性回归的区别
- 2.1在深度学习中，逻辑回归与线性回归的区别
3.什么是逻辑回归
4.什么是线性回归

一、线性回归简介

线性回归是指采用线性组合形式的回归模型，在线性回归问题中，因变量和自变量之间是线性关系的。对于第 i 个因变量xi，我们乘以权重系数wi，取y为因变量的线性组合：
$y = f (x) = W 1 X 1 + \cdot\cdot\cdot\cdot\cdot\cdot\cdot + Wn X n + b$

对于一个学习系统来说，我们需要找到最适合数据的模型，模型有很多，需要不断尝试，其中最简单的一个模型就是线性模型。

二、 Logistic回归简介

Logistic回归是一种常用的统计分析方法，通常用于解决二分类问题。它通过将线性回归模型的输出通过一个logistic函数（也称为Sigmoid函数）转换为0到1之间的概率值，从而进行分类预测。

在Logistic回归中，我们试图找到最佳的拟合参数，使得模型能够最好地拟合训练数据并对新样本做出准确的分类预测。通常使用最大似然估计或梯度下降等优化算法来训练Logistic回归模型。

与线性回归不同，Logistic回归适用于处理分类问题，例如判断邮件是否为垃圾邮件、患者是否患有某种疾病等。通过调整阈值，可以控制模型对正类和负类的分类边界，从而灵活地应对不同需求。

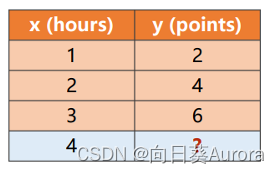
在这里插入图片描述

我们需要去找到一个w的取值，使得（ y ^ − y ） 2最小
y=w∗x可以采用穷举法求最优值w

代码如下：

import numpy as np
import matplotlib.pyplot as plt

#训练集数据
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

#定义线性模型y=wx
def forward(x):
    return x*w

#定义损失函数:loss=(y_predect-y)2=(x*w-y)2
def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

##定义w_list、mse_list来保存w对应的mes loss的取值
w_list = []
mse_list = []

#穷举法计算损失值cost
for w in np.arange(0.0,4.1,0.1):
    print("w=",w)
    l_sum = 0
    for x_val,y_val in zip(x_data,y_data):   #x,y拼接为[x,y]
        y_pred_val = forward(x_val)          #预测
        loss_val = loss(x_val,y_val)      #求损失loss
        l_sum += loss_val                    #loss求和
        print('\t',x_val,y_val,y_pred_val,loss_val)
    print("MSE=",l_sum/3)                    #计算mse
    w_list.append(w)
    mse_list.append(l_sum/3)

# 绘制图像
plt.plot(w_list, mse_list)
plt.xlabel('w')
plt.ylabel('Loss')
plt.show()

结果如下：

在这里插入图片描述

优化问题

梯度下降算法

在这里插入图片描述

在算法开始时会给参数w取一个初始值，然后不断更新，想要找到一个全局最优值，使得cost最小

需要去计算每个点的梯度。
• 梯度即微分（导数）
• >0:函数上升，损失值在增大，w应该减小（梯度的反方向运动）；
• <0：函数在下降，损失值在减小（目标方向），w应该增大（梯度的反方向运动）。
• 所以参数w的更新方向应该是梯度的负方向！

注意：梯度下降算法是一种贪心算法，得到的解不一定是全局最优。
• 解决：
• 运行多次，随机化初始点。（SGD：随机梯度下降）
• 梯度下降法的初始点也是一个超参数。

import matplotlib.pyplot as plt

# 训练集
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

# 初始化参数
w = 1.0

# 定义线性模型： y = w*x
def forward(x):
    return x * w

# 计算 MSE
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

# 计算梯度
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2*x*(x*w-y)
    return grad / len(xs)


epoch_list = []
cost_list = []
print('predict(before training)', 4, forward(4))
#epoch训练轮次，表示重复训练的次数
for epoch in range(100):  #训练100epoch
    cost_val = cost(x_data, y_data) #计算损失值
    grad_val = gradient(x_data, y_data)  #计算梯度
    w -= 0.01 * grad_val            #更新梯度（参数）0.01learning rate
    print('epoch', epoch, 'w=', w, 'loss=', cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)


# 绘制损失曲线
print('w= ', w)
print("predict(after training)", 4, forward(4))
plt.plot(epoch_list, cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()

损失曲线图

一般来说，用下图这种epoch、cost（loss）的损失值变化曲线来表示训练情况
在这里插入图片描述
在20 epoch以前，模型快速收敛，后面趋于稳定，损失值接
近0.这是理想的训练情况。
损失值随着训练越来越小，逐渐收敛，这次训练就是成功的。
如果损失值随着训练还逐渐增大了，那么训练就失败了！

随机梯度下降（Stochastic Gradient Descent）

• 梯度下降算法：用所有样本的平均损失值cost来更新参数；
• 随机梯度下降算法：随机选取N个样本中的一个样本的loss来更新参数！
• 随机梯度下降算法能够更好的解决鞍点问题，因为是随机选取一个样本的
loss，可能会跨过鞍点继续更新
在这里插入图片描述

import matplotlib.pyplot as plt

# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 初始化参数
w = 1.0

# 定义线性模型： y = w*x
def forward(x):
    return x * w

# 计算 MSE
def loss(x, y):
    y_pred = forward(x)  # 计算一个样本的损失值loss
    return (y_pred - y) ** 2

# 计算梯度SGD
def gradient(x, y):
    return 2 * x * (x * w - y)


epoch_list = []
loss_list = []
print('predict (before training)', 4, forward(4))

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        grad = gradient(x, y)
        w = w - 0.01 * grad   # 更新梯度
        print("\tgrad:", x, y, grad)
        l = loss(x, y)
    print("progress:", epoch, "w=", w, "loss=", l)
    epoch_list.append(epoch)
    loss_list.append(l)

# 绘制损失曲线
print('predict (after training)', 4, forward(4))
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

在这里插入图片描述

比较

在这里插入图片描述

三、用PyTorch实现Logistic

1 、
数据准备
线性方程
激活函数
损失函数
优化算法
模型可视化

""" #######  用PyTorch实现Losistic回归   ########"""
import numpy as np
import torch
from torch import nn
from torch.distributions import MultivariateNormal
import matplotlib.pyplot as plt



# 数据准备

# 设置两组不同的均值向量和协方差矩阵
mu1 = -3 * torch.ones(2)
mu2 = 3 * torch.ones(2)
sigma1 = torch.eye(2) * 0.5
sigma2 = 3 * torch.eye(2) * 2

# 各从两个多元高斯分布中生成100个样本
m1 = MultivariateNormal(mu1, sigma1)
m2 = MultivariateNormal(mu2, sigma2)
x1 = m1.sample((100,))
x2 = m2.sample((100,))

# 设置正负样本的标签
y = torch.zeros(200, 1)
y[100:] = 1

# 组合、打乱样本
x = torch.cat([x1, x2], dim=0)
idx = np.random.permutation(len(x))
x = x[idx]
y = y[idx]

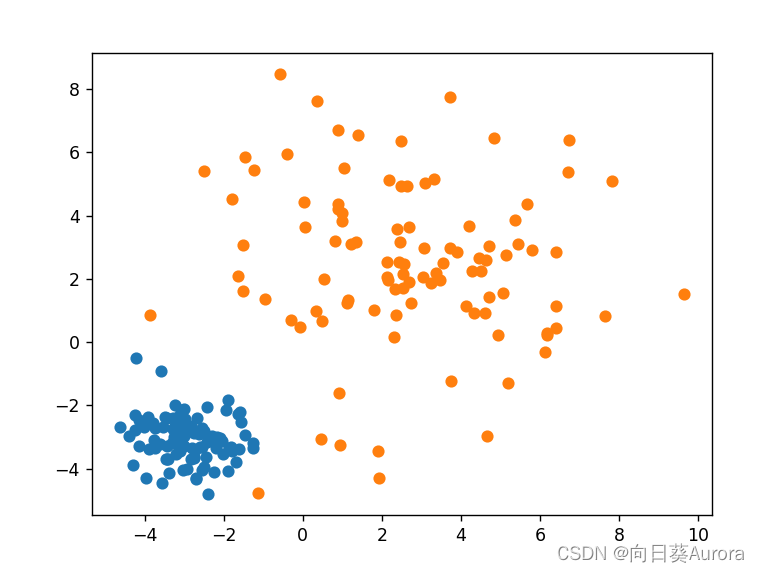
# 绘制样本
plt.scatter(x1.numpy()[:, 0], x1.numpy()[:, 1])
plt.scatter(x2.numpy()[:, 0], x2.numpy()[:, 1])
plt.show()

在这里插入图片描述

'''线性方程'''
D_in, D_out = 2, 1
linear = nn.Linear(D_in, D_out, bias=True)
output = linear(x)

print(x.shape, linear.weight.shape, linear.bias.shape, output.shape)


def my_linear(x, w, b):
    return torch.mm(x, w.t()) + b


torch.sum((output - my_linear(x, linear.weight, linear.bias)))


##激活函数
sigmoid = nn.Sigmoid()
scores = sigmoid(output)

def my_sigmoid(x):
    x = 1/(1 + torch.exp(-x))
    return x

torch.sum(sigmoid(output) - my_sigmoid(output))


'''损失函数'''
loss = nn.BCELoss()
loss(sigmoid(output), y)

def my_loss(x, y):
    loss = - torch.mean(torch.log(x) * y + torch.log(1 - x) * (1 - y))
    return loss

loss(sigmoid(output), y) - my_loss(my_sigmoid(output), y)

import torch.nn as nn

class LogisticRegression(nn.Module):
    def __init__(self, D_in):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(D_in, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.linear(x)
        output = self.sigmoid(x)
        return output
lr_model = LogisticRegression(2)
loss = nn.BCELoss()
loss(lr_model(x),y)




class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()
        self.linear1 = nn.Linear(1, 1, bias=False)
        self.linear2 = nn.Linear(1, 1, bias=False)

    def forward(self):
        pass

for param in MyModel().parameters():
    print (param)


'''优化算法'''
from torch import optim
optimizer =  optim.SGD(lr_model.parameters(), lr=0.03)
batch_size = 10
iters = 10
#for input, target in dataset:
for _ in range(iters):
    for i in range(int (len (x)/batch_size)):
        input =x[i*batch_size:(i+1)*batch_size]
        target = y[i*batch_size:(i+1)*batch_size]
        optimizer.zero_grad()
        output =lr_model(input)
        l = loss(output, target)
        l.backward()
        optimizer.step()



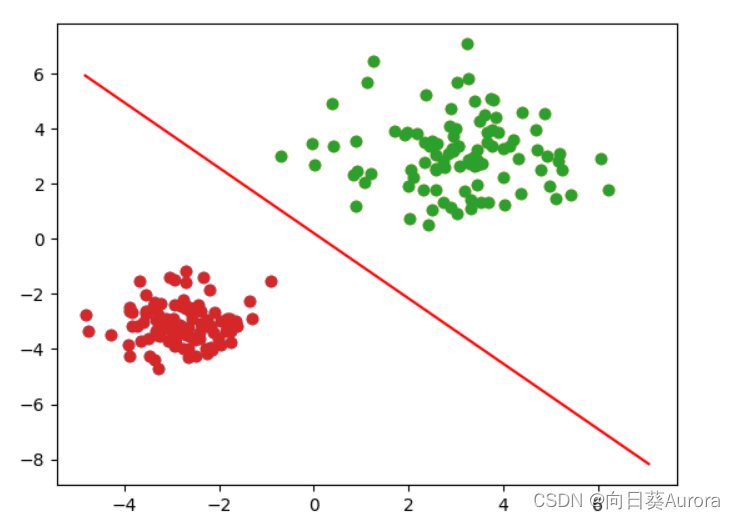
'''模型可视化'''
# pred_neg = (output <= 0.5).view(-1)
# pred_pos = (output > 0.5).view(-1)
# plt.scatter(x[pred_neg, 0], x[pred_neg, 1])
# plt.scatter(x[pred_pos, 0], x[pred_pos, 1])


pred_neg = (output <= 0.5).view(-1)
pred_pos = (output > 0.5).view(-1)
plt.scatter(x[pred_neg.nonzero(), 0], x[pred_neg.nonzero(), 1])
plt.scatter(x[pred_pos.nonzero(), 0], x[pred_pos.nonzero(), 1])


w = lr_model.linear.weight[0]
b = lr_model.linear.bias[0]

def draw_decision_boundary (w, b, x0):
    x1 = (-b- w[0] * x0) /w[1]
    plt.plot(x0.detach().numpy(),x1.detach().numpy(),'r')

draw_decision_boundary(w, b, torch.linspace(x.min(), x.max(),50))
plt.show()

在这里插入图片描述

笔记

1.反向传播

反向传播是深度学习中常用的优化算法，用于调整神经网络中的参数以最小化损失函数。它通过计算损失函数对每个参数的梯度，然后沿着梯度的反方向更新参数值，从而使得损失函数达到最小值。
具体而言，反向传播包括两个主要步骤：前向传播和反向传播。在前向传播中，输入数据通过网络，经过一系列的线性变换和非线性变换，最终得到输出结果。在这个过程中，网络会记录下每一层的中间变量，以便在反向传播时使用。在反向传播中，首先计算损失函数对输出的梯度，然后利用链式法则依次计算每一层参数的梯度，并利用梯度下降等优化方法更新参数。
反向传播算法的提出极大地推动了神经网络的发展，使得训练深层网络变得可行。它是深度学习中的核心算法之一，被广泛应用于图像识别、自然语言处理等领域。

2.逻辑回归与线性回归的区别

逻辑回归和线性回归在统计学和机器学习中有着不同的应用和特点：

应用领域：
• 线性回归通常用于预测连续型的数值，比如房屋价格、销售额等。它试图找到自变量和因变量之间的线性关系。
• 逻辑回归则主要用于处理分类问题，例如二元分类（是/否）或多元分类（多个类别之间的区分）。它输出的是样本属于某个类别的概率。
输出值：
• 线性回归的输出是连续的实数，可以是任意实数。
• 逻辑回归的输出是介于0和1之间的概率值，通常表示为样本属于某一类别的概率。
模型形式：
• 线性回归模型假设因变量与自变量之间存在线性关系，其模型形式是 y = β0 + β1x1 + β2x2 + … + ε。
• 逻辑回归模型使用逻辑函数（sigmoid函数）将线性组合的结果映射到0-1之间，其模型形式是 p = 1 / (1 + e^(-z))，其中 z = β0 + β1x1 + β2x2 + …。
参数估计方法：
• 线性回归通常使用最小二乘法进行参数估计，目标是最小化观测值与模型预测值之间的残差平方和。
• 逻辑回归通常使用极大似然估计进行参数估计，通过最大化观测数据出现的可能性来估计模型参数。
总的来说，逻辑回归和线性回归虽然都包含“回归”两字，但是在应用场景、输出值和模型形式上有着明显的区别。

2.1在深度学习中，逻辑回归与线性回归的区别

在深度学习中，逻辑回归和线性回归的区别与传统统计学和机器学习中的区别类似，但在深度学习框架下有一些特殊的考虑因素：

模型结构：
• 在深度学习中，逻辑回归通常被视为单层神经网络，其输出通过一个逻辑（sigmoid）函数来实现二元分类。
• 线性回归也可以看作是一个最简单的神经网络模型，只有一个输入层和一个输出层，没有激活函数。
激活函数：
• 在深度学习中，逻辑回归使用sigmoid函数作为激活函数，将输出限制在0到1之间，表示样本属于某一类别的概率。
• 线性回归在深度学习中通常不使用激活函数，直接输出线性组合的结果。
参数更新：
• 在深度学习中，逻辑回归和线性回归通常使用梯度下降或其变种算法进行参数更新。
• 由于深度学习中通常涉及大量参数和多层结构，参数更新可能会涉及更复杂的优化算法和技巧。
尽管在深度学习框架下，逻辑回归和线性回归有一些特定的实现方式和细微差别，但它们仍然保持了在传统机器学习中的基本概念和特点。深度学习中的逻辑回归可以作为简单的二分类模型，而线性回归可以用于回归问题或作为深度学习模型的一部分。

3.什么是逻辑回归

逻辑回归是一种常见的统计学习方法，用于解决分类问题。尽管名字中包含"回归"一词，但逻辑回归实际上是一种分类算法，主要用于处理二元分类（是/否）或多元分类问题。
逻辑回归的基本原理是通过对特征的线性组合进行建模，并将结果映射到一个介于0和1之间的概率值，表示样本属于某一类别的概率。逻辑回归模型使用逻辑函数（sigmoid函数）来实现这一映射，数学上表达为：
[ P(y=1|x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \beta_2x_2 + … + \beta_nx_n)}} ]
其中：
• ( P(y=1|x) ) 表示在给定输入特征 x 的条件下，样本属于类别 1 的概率。
• ( e ) 是自然对数的底。
• ( \beta_0, \beta_1, \beta_2, …, \beta_n ) 是模型参数，通过训练数据学习得到。
• ( x_1, x_2, …, x_n ) 是样本的特征值。
逻辑回归通常使用最大似然估计或梯度下降等优化算法来学习模型参数，以使模型的预测尽可能符合实际观测数据。训练完成后，逻辑回归模型可以用来对新样本进行分类预测，输出的概率值可以作为判断样本类别的依据。
逻辑回归在实际应用中非常广泛，特别适用于二元分类问题，如信用风险评估、疾病诊断、文本分类等领域。它简单、易于理解，并且具有较好的性能表现。

4.什么是线性回归

线性回归是一种用于建立和预测变量之间线性关系的统计学习方法。它通常用于预测因变量（目标变量）和一个或多个自变量（特征）之间的关系。在简单线性回归中，只有一个自变量；而在多元线性回归中，可以有多个自变量。
线性回归的基本原理是假设因变量 ( y ) 与自变量 ( x ) 之间存在线性关系，并通过拟合出最佳的线性方程来进行预测。数学上，简单线性回归模型可以表示为：
[ y = \beta_0 + \beta_1x + \varepsilon ]
其中：
• ( y ) 表示因变量（要预测的变量）。
• ( x ) 表示自变量（特征）。
• ( \beta_0 ) 和 ( \beta_1 ) 是线性回归模型的参数，分别表示截距和斜率，通过拟合数据得到。
• ( \varepsilon ) 表示误差项，代表了模型无法解释的随机误差。
通过最小化实际观测值与模型预测值之间的差异（通常使用最小二乘法），可以得到最优的参数估计，从而建立线性回归模型。这个模型可以用于预测新的自变量对应的因变量的取值。
线性回归在许多领域都有广泛的应用，包括经济学、金融学、社会科学和自然科学等。它提供了一种直观且有效的方法来研究和预测变量之间的关系，但需要注意的是，线性回归假设了因变量和自变量之间的关系是线性的，因此在应用时需要谨慎选择适合的模型。

向日葵Aurora

关注

20
点赞
踩
18

收藏

觉得还不错? 一键收藏
1
评论
Logistic回归（第五章）

线性回归是指采用线性组合形式的回归模型，在线性回归问题中，因变量和自变量之间是线性关系的。yfxW1X1⋅⋅⋅⋅⋅⋅⋅WnXnbyfxW1X1⋅⋅⋅⋅⋅⋅⋅WnXnb对于一个学习系统来说，我们需要找到最适合数据的模型，模型有很多，需要不断尝试，其中最简单的一个模型就是线性模型。Logistic回归是一种常用的统计分析方法，通常用于解决二分类问题。
复制链接

扫一扫