深蓝视觉slam

三维空间的刚体运动：

欧式变换：通过R T两个量来表示不同矩阵在空间中的位置关系。R为旋转 T为平移。

这时可以用一个矩阵T表述其中的转换关系，T表述旋转和平移两种操作

旋转向量

任意旋转都可以用一个旋转轴和一个旋转角来表示，于是有了旋转向量。使用一个向量，其方向与旋转轴一致，长度等于旋转角。旋转向量就是下节要讲的SO(3)的李代数so(3)，而变换矩阵的李代数则是se(3)旋转向量是三维的，变换矩阵的是6维（三维旋转+三维平移）

四元数

四元数是一种紧凑的无奇异的表述三维向量的方式。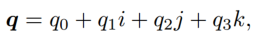

i，j，k为三个虚部，他们满足关系式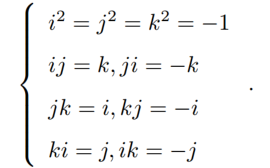

由于其特殊性，有时候也采用一个标量一个向量的形式来表达四元数

Eigen

Eigen是一个矩阵运算库，这部分其实不难，有个学习的例程，照着敲敲就会了，分享一个例子。
链接：百度网盘 请输入提取码
提取码：k9p2

 QR分解：用来解决矩阵线性方程Ax=b;QR 分解可以应用于许多数值计算问题中，包括线性方程组求解、最小二乘问题、特征值计算等。通过 QR 分解，我们可以更方便地处理这些问题，例如，对于线性方程组 (Ax = b)，我们可以将其表示为 (QRx = b)，然后解出 (Rx = Q^T b)。在数值计算中，通常使用 Householder 变换或 Givens 变换等方法来实现 QR 分解。

Eigen:中使用QR分解 解方程：

 Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
    matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
    Eigen::Matrix< double, MATRIX_SIZE,  1> v_Nd;
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);

示例： 

答案： 

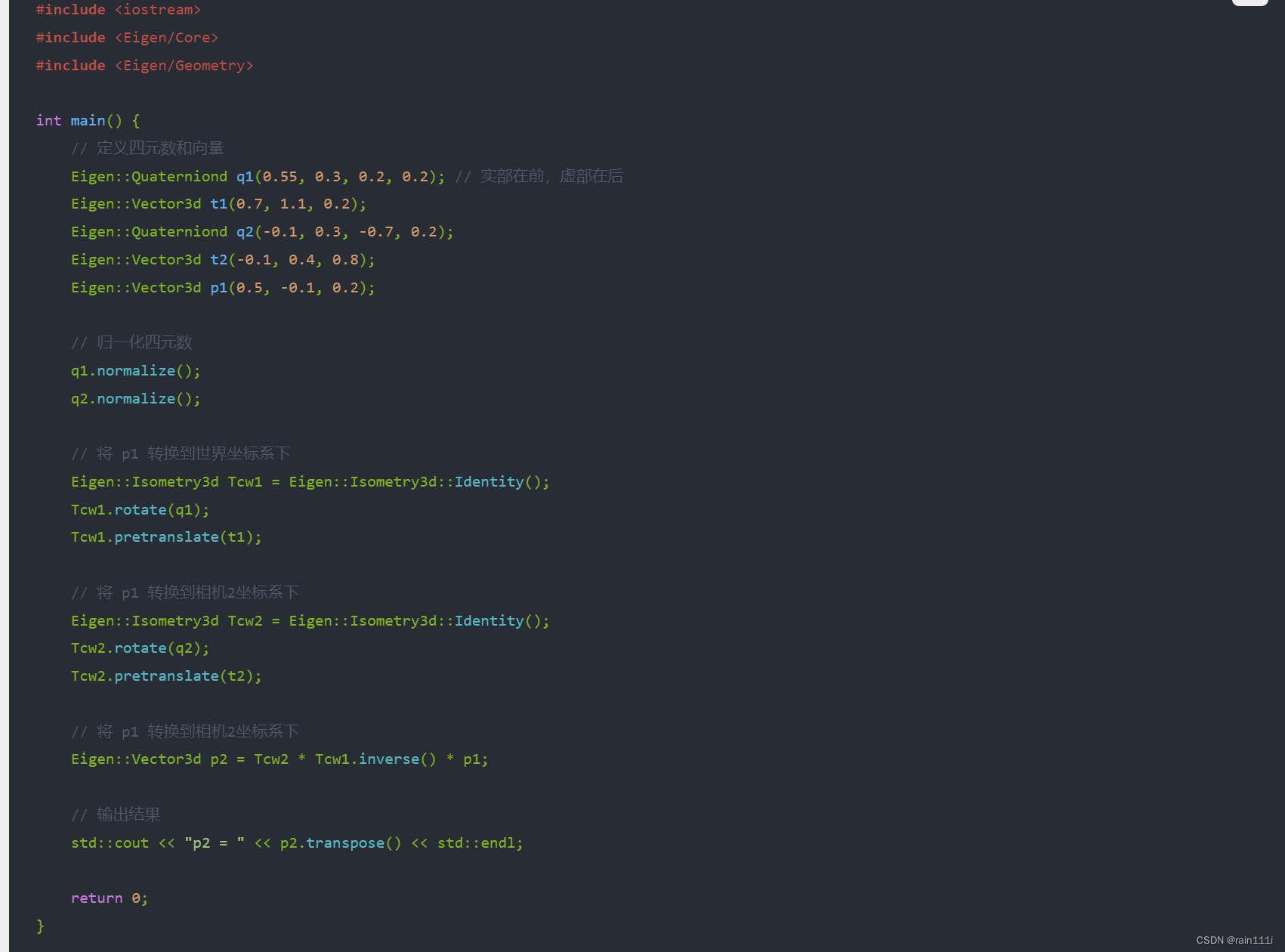
1. Tcw1.inverse(): 这一部分使用了 inverse() 方法来计算矩阵 (T_{cw1}) 的逆矩阵。在这里，(T_{cw1}) 表示相机1坐标系到世界坐标系的变换矩阵。求逆操作的结果是得到了世界坐标系到相机1坐标系的变换矩阵，即相机1的位姿。

2. Tcw2 * Tcw1.inverse(): 这一部分将相机2的位姿 (T_{cw2}) 与相机1的位姿 (T_{cw1}) 的逆矩阵相乘。这个操作可以将相机1的坐标系变换到世界坐标系下，然后再将其变换到相机2的坐标系下，即实现了从相机1坐标系到相机2坐标系的转换。

3. p1: 这是一个三维向量，表示在相机1坐标系下的一个点。

4. Tcw2 * Tcw1.inverse() * p1: 这一部分将上述得到的相机1坐标系下的点 (p_1)，通过相机2的位姿变换 (T_{cw2} * T_{cw1}^{-1})，转换到相机2的坐标系下，得到了相机2坐标系下的点 (p_2)。

最终，p2 表示了在相机2坐标系下的经过坐标变换后的点。这个操作常用于在多相机系统中将特征点或物体点的坐标从一个相机的坐标系转换到另一个相机的坐标系下。

总结：tcw是用来表示一个坐标系的变换，就是相机坐标与世界坐标系的关系。对于 Tcw2 * Tcw1.inverse() * p1这句话，就是首先计算相机1标系到相机2坐标系的转换坐标系的转换，然后*p1就可以得到坐标系2下的p1的坐标。相机2->世界*世界->相机1=相机1->相机2

   李群和李代数：视觉slam爬坑——高翔深蓝学院——第三讲——李群与李代数_反对称符号看作叉积-CSDN博客

使用目的：引入李群和李代数是解决什么样的相机位姿符合当前的观测数据，即求解最优R，t。使误差最小化的问题。
旋转矩阵有一定的约束性（正交且行列式为1），他们作为优化变量的时候会引入额外的约束，通过李群和李代数的转换关系，将位姿估计变成无约束的优化问题

1.群的定义
为什么引入李群这种东西，旋转矩阵R和变换矩阵T不是可以表示机器人的旋转和平移特性吗？
首先给群下个不完全的定义：群是为了描述满足一类性质的矩阵的集合。满足三维旋转矩阵定义和性质的构成特殊正交群SO(3)、满足变换矩阵定义和性质的构成特殊欧式群SE(3)
他们两个的定义如下：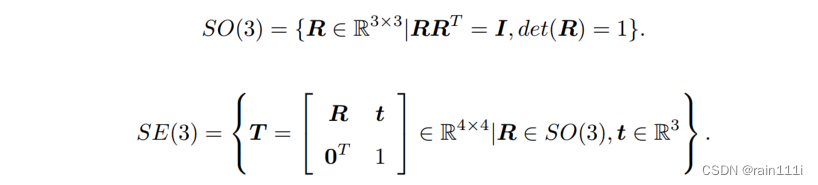

正式定义：

ps:这里对群的定义是针对SO3和SE3的特定的，只要满足一种集合加上一种运算的代数结构都可为群，例如{Z,+}也为群，但不是李群了
同时请思考为什么旋转矩阵的加法为什么不是群？
首先什么是旋转矩阵来着？旋转矩阵要满足下面性质：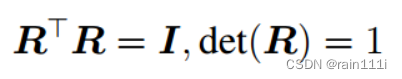

行列式为1，且是正交矩阵，不存在R1+R2或者T1+T2还满足这个性质，但是存在R1R2或者T1T2还满足这个性质的（可以看作做了两次旋转）。

那么李群是什么？
李群是指具有连续（光滑）性质的群。像整数群 Z 那样离散的群没有连续性质，所以不是李群。而 SO(n) 和 SE(n)，它们在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动，所以它们都是李群。由于 SO(3) 和 SE(3) 对于相机姿态估计尤其重要，我们主要讨论这两个李群。

2.李代数
前边一直逼逼叨叨说的李代数是什么鬼？
   相机在三维空间中是连续的旋转或者变换的，而我们SLAM目的就是优化求解相机的这个最佳的位姿T（变换矩阵）。它观测到一个惯性坐标系下点p产生了一个观测数据z，z是相机坐标系下的坐标，则可得到z=Tp+w，w是观测噪声（误差），w=z-Tp。

机器人的位姿估计就转变成寻找一个最优的T使得整体的误差最小化由于要对T（矩阵）求导，所以要引入变量时间变量t，经过一系列的错做后就得到了李代数向量ϕ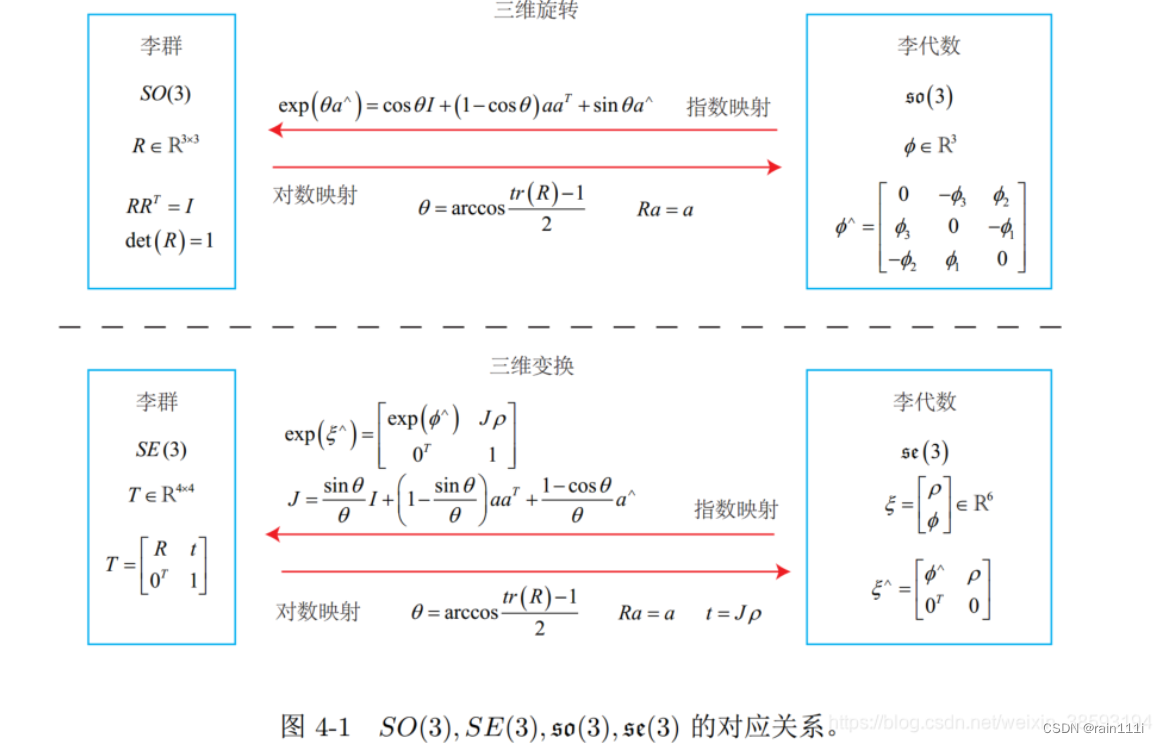

我们为什么用李代数呢？是因为无法直接对变换\旋转矩阵求导——>那不能求导怎么办？引入时间变量t，无法对矩阵求导可以对t求导——>对t求导后解决什么问题呢？解决在局部连续的时间内对误差的线性优化问题。对，李代数的引入就是为了解决状态估计过程中的优化问题。

现在我们已经解决求导的问题了。两次连续的旋转可以用矩阵乘法来描述，但用李代数如何表示呢？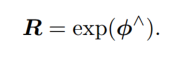

则两次连续的矩阵乘法可表示为：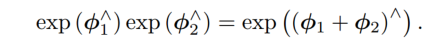

相机模型:视觉slam爬坑——高翔深蓝学院——第四讲——相机模型_深蓝学院双目相机-CSDN博客

内参：物理成像平面和像素平面的关系描述

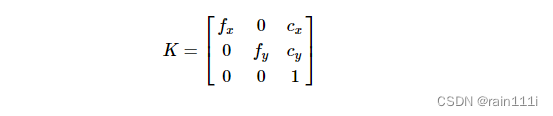
K有4个未知数和相机的构造相关，fx,fy和相机的焦距，像素的大小有关；cx,cy是平移的距离，和相机成像平面的大小有关。

 求解K的过程叫做相机的标定，通常认为，相机的内参在出厂之后是固定的，不会在使用过程中发生变化。有的相机生产商会告诉相机的内参，而有时需要自己确定相机的内参，也就是所谓的标定。标定算法已成熟，在网络上可以找到大量的标定教学。

外参数

其中，p是图像中像点的像素坐标，K是相机的内参数矩阵，P是相机坐标系下的三维点坐标。
上面推导使用的三维点坐标是在相机坐标系下的，相机坐标系并不是一个“稳定”的坐标系，其会随着相机的移动而改变坐标的原点和各个坐标轴的方向，用该坐标系下坐标进行计算，显然不是一个明智的选择。需要引进一个稳定不变坐标系：世界坐标系，该坐标系是绝对不变，SLAM中的视觉里程计就是求解相机在世界坐标系下的运动轨迹。

设Pc是P在相机坐标系坐标，Pw是其在世界坐标系下的坐标，可以使用一个旋转矩阵R和一个平移向量t，将Pc变换为Pw      

外参就是T（R和t），外参会随着机器人的运动而改变。

                                                       

畸变： 

平面上的任意一点p可以用笛卡尔坐标表示为[x,y]T，也可以写成极坐标的形式[r,θ]T， 
其中r表示点p离坐标系原点的距离，θ表示和水平轴的夹角。 

 

k1、k2、k3为径向畸变系数；p1、p2为切向畸变系数。
相机畸变现象发生的位置：
①世界坐标系 -> 相机坐标系：刚体变换，不存在畸变现象；
②相机坐标系 -> 图像坐标系：也就是成像过程，理想情况下是相似三角形，但实际由于相机智造、装配的原因，成像过程存在畸变现象；
③图像坐标系 -> 像素坐标系：坐标原点、单位不同，仅仅平移与缩放，不存在畸变现象。

双目相机：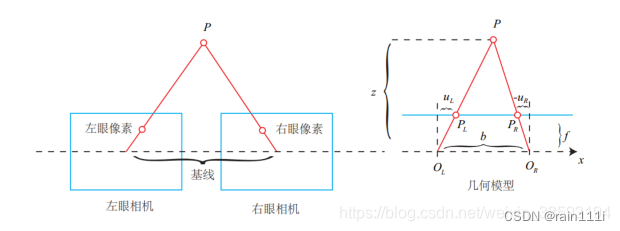 

题目： 

答案：

#include <opencv2/opencv.hpp>
#include <vector>
#include <string>
#include <Eigen/Core>
#include <pangolin/pangolin.h>
#include <unistd.h>

using namespace std;
using namespace Eigen;

// 左眼+右眼 图象
string left_file = "/home/robot/桌面/slambook2-master/ch5/stereo/left.png";
string right_file = "/home/robot/桌面/slambook2-master/ch5/stereo/right.png";

// 在pangolin中画图，已写好，无需调整
void showPointCloud(
    const vector<Vector4d, Eigen::aligned_allocator<Vector4d>> &pointcloud);

int main(int argc, char **argv) {
    // 1. 设置参数
    // 内参
    double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;
    // 基线
    double b = 0.573;

    // 2. 读取图像
    cv::Mat left = cv::imread(left_file, 0);
    cv::Mat right = cv::imread(right_file, 0);
    cv::Ptr<cv::StereoSGBM> sgbm = cv::StereoSGBM::create(
        0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32);    // 神奇的参数
    
    // 3. 处理
    cv::Mat disparity_sgbm, disparity;
    // 通过sgbm将两个图像经过计算传给disparity_sgbm，然后disparity_sgbm->disparity
    sgbm->compute(left, right, disparity_sgbm);
    disparity_sgbm.convertTo(disparity, CV_32F, 1.0 / 16.0f);

    // 4. 声明点云
    vector<Vector4d, Eigen::aligned_allocator<Vector4d>> pointcloud;

    // 5. 计算。如果你的机器慢，请把后面的v++和u++改成v+=2, u+=2
    for (int v = 0; v < left.rows; v++)
        for (int u = 0; u < left.cols; u++) {
            if (disparity.at<float>(v, u) <= 0.0 || disparity.at<float>(v, u) >= 96.0) continue;

            Vector4d point(0, 0, 0, left.at<uchar>(v, u) / 255.0); // 前三维为xyz,第四维为颜色

            // 根据双目模型计算 point 的位置
            double x = (u - cx) / fx;
            double y = (v - cy) / fy;
            double depth = fx * b / (disparity.at<float>(v, u));
            point[0] = x * depth;
            point[1] = y * depth;
            point[2] = depth;

            pointcloud.push_back(point);
        }

    cv::imshow("disparity", disparity / 96.0);
    cv::waitKey(0);
    // 画出点云
    showPointCloud(pointcloud);
    return 0;
}

void showPointCloud(const vector<Vector4d, Eigen::aligned_allocator<Vector4d>> &pointcloud) {

    if (pointcloud.empty()) {
        cerr << "Point cloud is empty!" << endl;
        return;
    }

    pangolin::CreateWindowAndBind("Point Cloud Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
        pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
        pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
        .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
        .SetHandler(new pangolin::Handler3D(s_cam));

    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glPointSize(2);
        glBegin(GL_POINTS);
        for (auto &p: pointcloud) {
            glColor3f(p[3], p[3], p[3]);
            glVertex3d(p[0], p[1], p[2]);
        }
        glEnd();
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
    return;
}

 批量状态估计问题：

为什么需要引入最优化，无约束非线性优化等方法呐？
解决状态估计问题，为什么要进行状态估计？
由于噪声的存在，运动方程（相机成像）和观测方程（位姿由T描述，用李代数来优化）的等式不是精确的。

状态估计的方式:

增量/渐进(incremental)：(滤波器）观测和运动数据是随时间逐渐到来的，我们应持有一个当前时刻的状态估计，然后用新的数据来更新它。
批量(batch)：把0-k时刻的所有输入和观测数据放在一起，估计0-k时刻的轨迹和地图。
显然批量是不实时的，所以我们采用折中的办法：滑动窗口法：固定一些历史轨迹，仅对当前时刻的一些轨迹进行优化。

 视觉里程计： 

通过两个图片，交给算法然后得出运动前后的位姿变换。

特征点法：

Fast特征点：以半径为3画圆，检测周围一圈一共16个点，设定阈值。有12个连续的点与该点亮度差超过阈值，确认为一个Fast特征点。（快速检测方式是先检查上下左右四个点，有三个点大于阈值才有可能是角点。因为要的是“连续”的点。有一个断掉了，就不能是连续的12个点了；然后通过非极大值抑制的方式筛选掉多余的点）

ORB特征点：改进fast特征点，具体是定义图像块的矩（mpq，p、q=0或1）

特征点匹配：

（1）暴力匹配，用汉明距离（描述子的不同位数）计算描述子距离，最近的作为匹配点。

（2）快速近似最近邻（FLANN）算法，这个书里没写细节。

初步筛选错误匹配：

经验方式：给定一个最小距离，如果汉明距离小于最小距离的两倍，就认为匹配没有太大的问题。

2D-2D

即点对都是2D点，比如单目相机匹配到的点对。我们可以用对极几何来估计相机的运动。在估计完相机运动之后，我们还可以用三角测量（Triangulation）来估计特征点的空间位置（包括深度）。注意，是估计相机之间的运动（注意与3D-2D不同）。

走到现在这里，特征点已经匹配出来了。也就是说，我们现在得到了一些像素点的配对（p1，p2）……想要根据这个恢复R和t。

接下来主要两个内容，对极几何求位姿，三角测量用求出来的位姿求深度。

对极几何：
关于这块，高博的书里像素坐标用的是p1，p2，归一化平面坐标用的x1，x2。其实我觉得这两个符号换换更好。另外公式一堆，对于我来说，我觉得有点抓不住重点。我按适合自己的顺序总结一下：

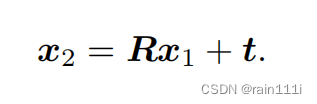
一个点，在两个归一化坐标平面表示为x1和x2，用R和t像上面这样建立起联系来。

两边都左乘t^，t^乘以一个向量，相当于t和这个向量做叉乘，产生的新的向量垂直于t和另一个向量（右手定律嘛）

另外，自己和自己叉乘结果是0

就得到了这个：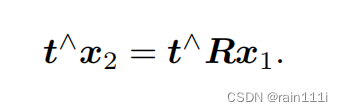

这时候我们是想让它一边为0，好求R和t

注意等式左边，t^x2产生的向量，垂直于二者，那么t^x2再左乘一个x2T，就是两个垂直的向量求内积，结果是0

所以得到下式：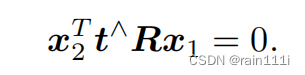

上面这玩意就是对极几何，t^R表示成E，这个E就是本质矩阵（Essential Matrix）。

不过我们刚开始说了，特征点匹配以后得到的是两个像素坐标系下的点p1和p2，并不是x1和x2，两者之间差了个内参K的。

我们知道归一化平面上的点，左乘个内参就是像素平面上的点了，也就是说p=Kx，那么x就等于K-1 p

因此上面的式子变成了：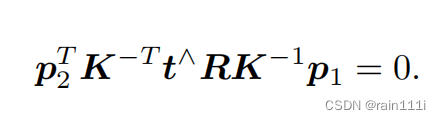

把p留下来，中间的写成F，这个F就是所谓的基础矩阵（Fundametal Matrix）

所以总结为：两边是两个像素点，中间就是基础矩阵F（太基础了，不能再往深里化了）；两边是两个归一化点，中间就是本质矩阵E。

其实E和F是一码事，因为内参K基本已知。二者求出一个就行了。

书中给出的是求本质矩阵E的过程。求法就是直接设一个E矩阵，九个点分别是e1……e9，两边设两个归一化的点的向量，展开乘，化出一个线性方程组的形式。大小是8*9。（除掉了一个常数，最后一个是1。实际上只需要最少5个点，因为t^R一共6个自由度，又去掉了一个常数。但是为了解这个方程，所以用8个点）（8对点求解出来E，然后就可以通过E求解出来R t）

走到这里，E就求解出来了。但是E并不等同于位姿，因为E是t^R，想知道确切的位姿，需要拆开E，这个用的方法是SVD分解(奇异值分解)，就用上面说的E的奇异值性质，给了一个先验知识，说是E的奇异值满足[σ，σ，0]T的形式。分解出来是4个解，但是只有一个对于两个相机而言，都是正的深度。关于这块，高博书里写的是相当的含糊，我这里放个截图：

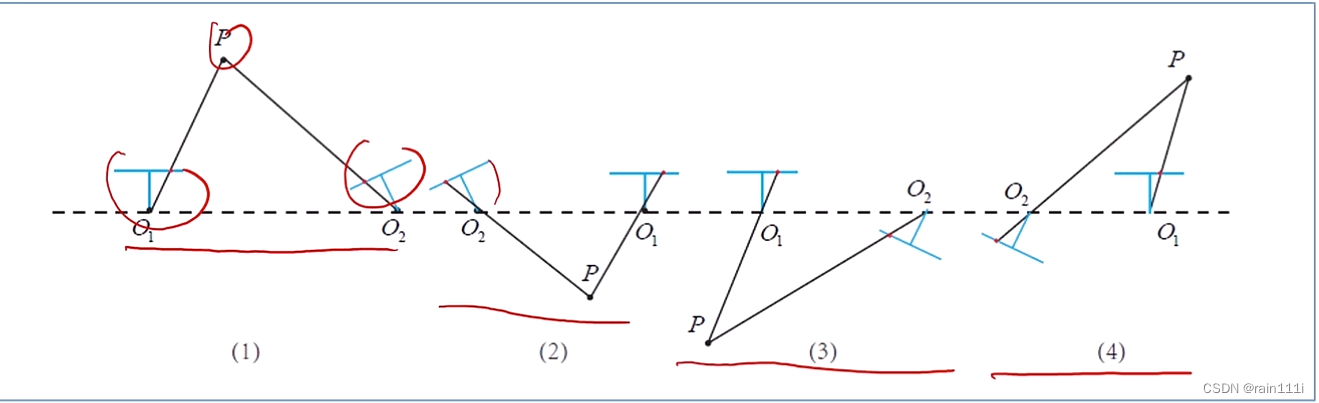
 （1）为正确。

单应矩阵H

单应矩阵(Homography)的意义在于避免“退化”现象造成基础矩阵自由度下降的问题。一般出现退化现象是因为特征点共面或者相机发生纯旋转。对于纯旋转的情况，E=t^R，纯旋转意味着t是0，那么E就是0，根据E恢复R就完全无从谈起。对于特征点共面的情况，算H大概是更方便一些吧（即特征点在同一个平面下使用H）；使用情况：无人机在天上对一个广阔的平面进行slam初始化。特征点都在一个平面上，这个时候用单应矩阵效果会好一点。

3D-2D 

最开始先直接总结下：

PnP（Perspective-n-Point）是求解3D到2D点对运动的方法。它描述了当知道n个3D空间点及其投影位置时，如何估计相机的位姿。注意是相机的位姿，而不是相机两帧之间的运动。

如果两张图像中的一张的特征点的3D位置已知，则最少只需要3个点对（以及额外的一个用于验证结果）就可以估计相机运动（位姿）。在双目或RGBD的视觉里程计中，我们可以直接使用PnP估计相机运动。而在单目视觉里程计中，必须先进行初始化（特征点匹配），才能使用PnP。3D-2D的PnP不需要对极约束，又可以在很少的匹配点中获得较好的运动估计，是一种最重要的姿态估计方法。

这部分的内容的前提是一个点的3D坐标已知，另一个只知道在图像上的2D点坐标。

书里只介绍了直接线性变换法、P3P、非线性优化（Bundle Adjustment）三种。

第一种就是根据线性代数直接算，硬刚；第二种P3P是已知三个点的世界坐标和这三个点的像素坐标，把这三个点的相机坐标系下的坐标算出来，转换成ICP问题；第三种是非线性优化，最小化重投影误差来解决（这种是把相机位姿和空间点位置都看成优化变量）。

带有匹配信息的3D-3D位姿求解非常容易，但是P3P存在一些问题：

1. P3P只利用了3个点的信息，当给定的点的配对点多于3组时，难以利用更多的信息。
2. 如果3D点或者2D点受噪声印象，或者存在误匹配，则算法失效。

 ------------------------------------------------------------------------------

P3P:

这个看图比较头疼，简化了很多符号。总体上是用余弦定理做的：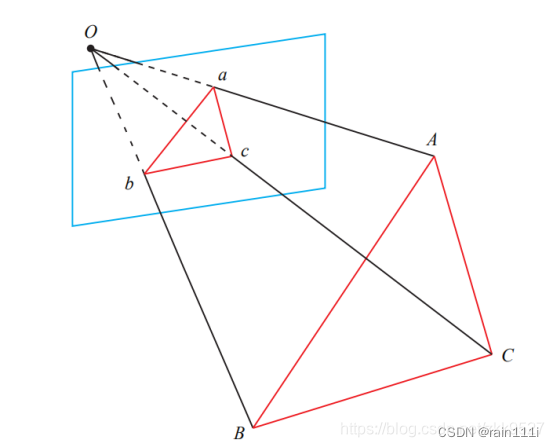

以上的图，OA,OB,OC是未知量。x=OA/OC,y=OB/OC，用余弦定理得到：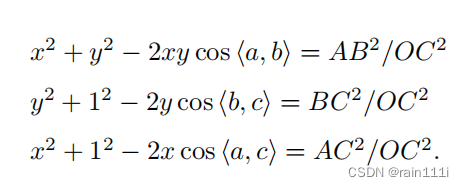

把等式右侧的三项设为v，u*v，w*v，u=BC2/AB2，w=AC2/AB2是已知的，cos都已知，那么目前是x，y不知道，v不知道。把第一个式子代入后俩，消去v，式子变成：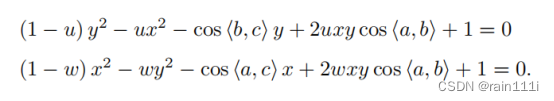

求出x，y以后，代入第上面三个式子中的第一个，可以求出v，v是AB2/OC2，就可以求出OC，别的也就依次都知道了。

关于这点，有几个值得注意：

1.cos值如何已知？

2D点图像位置已知，光心位置已知，可以计算其夹角，进而计算余弦。

2.求出的OA,OB,OC是什么？

可以当成是场景深度。场景深度和第三维的s是不一样的，s也是深度，但不是距离光心的深度，应该是所在平面距离光心所在平面的深度。但是可以互相求解。

3.之后怎么解位姿？

相机坐标系下3D坐标已知，可以据此求解3D-3D的ICP问题。

Bundle Adjustment（用来矫正误差）
这个内容是构建重投影误差，让重投影误差（观测值减去预测值）最小化。把相机位姿和空间点位置都看成优化变量，那么重投影误差函数相当于有两个自变量，一个是位姿，一个是对空间点P的位置求导。记P变换到相机坐标系下的位置是P'。

如果是对位姿求偏导，用扰动的方式，误差e先对P'求偏导，P’再对位姿的李代数求偏导，两个分开得到两个雅克比矩阵，然后乘在一起，得到一个2*6的雅克比矩阵。这样就求得了误差函数对位姿的导数矩阵。关于这里的雅克比矩阵，是比较重要的，因为g2o源码里显式的给出了雅克比矩阵的定义，如果不理解雅克比矩阵是怎么求出来的，代码就不能看懂。只当成黑盒子调用的话，理解不够深入。这个雅克比矩阵在后面的光度误差里面还会重复出现，因此我总结了一下：SLAM14讲学习笔记（五）视觉里程计（光流法和直接法）和对于雅克比矩阵的理解，看到这里的人一定要看一下这节！

如果是对P求偏导，第一项也是e先对P’求偏导，第二项P‘对P求偏导结果就是个旋转矩阵R，因此这部分的导数矩阵就是第一项和R相乘。

综上，都是加一个小量扰动，然后通过求解对于小量的偏导，从而解决不能直接求偏导的问题。

 3D-3D：ICP

迭代最近点（Iterative Closest Point，ICP），是根据一组配对好的3D点，比如两幅RGBD图像的匹配，求解两组点之间的变换关系，也就是相机的运动，跟相机模型没有关系K。和PNP类似，ICP的求解也分为两种方式：利用线性代数的求解（主要是SVD奇异值分界），以及利用非线性优化方式的求解（类似于BA）

此处也有2个方法：（SVD,非线性优化）

可以混合使用PnP和ICP，深度已知就用ICP算法