基于频率和混合解耦偏振的多倍相位超表面全息

解决的问题：传统的光学全息技术在动态显示、多倍相位调控和多功能集成方面受到限制，尤其是现有技术依赖非线性效应的多倍相位调控需要高功率激光和精确天线设计，难以实现高效率、低复杂度的全息显示。多倍相位调控的低能量效率和复杂条件制约了其实际应用。

提出的方法：本文提出了一种基于频率和偏振混合解耦的多倍相位超表面全息显示策略。通过单层介质超表面，结合Adam算法，设计了多倍相位全息生成循环，优化了基本相位分布及其多倍相位分布。利用圆偏振与线偏振的解耦设计，基于几何相位原理构建了超表面单元结构，实现了800 nm与1000 nm波长下分别通过交叉偏振和共偏振通道生成1倍、3倍、2倍和6倍的多倍相位全息图像。通过全息重建技术，赋予光束方向激励、折射和轨道角动量转换等功能。

实现的效果：实验验证表明，设计的超表面成功生成了四种完全不同的多倍相位全息图像，包括K=1、3、2和6倍的图像重建，量化误差低于4%。超表面在近红外波段的交叉偏振和共偏振通道均表现出稳定的多倍相位控制能力，同时优化的设计提升了空间带宽积，显著降低了实验复杂性。

创新点分析： 本文的创新性体现在硬件设计创新和算法创新的结合上。一方面，通过单层介质超表面实现了多倍相位调控的新机制，摆脱了传统非线性方法的高能量需求；另一方面，基于Adam优化的多倍相位全息生成算法，使得全息设计更加高效和可控。该方法显著提升了全息图像生成的效率和精度，为动态光学显示、全息加密和多功能光学器件设计提供了新的解决方案。

摘要：

超表面是一种人工智能平面光学器件，通过优化纳米结构和阵列设计实现优异功能。超表面已成为制造集成化、小型化光学系统的首选方法，为实现多维调制光学器件提供了微纳米级解决方案。在此，结合可切换的光学频率与混合圆偏振和线偏振状态，展示了多倍相位全息的实现。原始的全息相位分布可以通过自适应动量梯度下降算法进行反向优化。当相位值是原始值的若干倍时，可以重建完全不同的图像。通过优化介质超表面的结构分布，结合可变的入射光频率和解耦的圆偏振与线偏振，实现了多倍相位调制。不同偏振组合增强了多种全息调制的灵活性。该技术为动态多倍光束方向折射与激励、轨道角动量通信、多倍全息显示、光学加密与伪装、光开关与整形等提供了新解决方案。

结论：

在本研究中，我们设计了一种单层多倍相位超表面，用于重建由离散频率照明和偏振引起的全息图。利用基于Adam优化循环的优化算法生成基本相位全息图，并重建任意倍数的基本相位以显示任意图像。获得的仿真和实验结果符合预期。通过选择性频率与解耦的圆偏振和线偏振，实现了动态调制，以显示多倍全息重建。所提出的方法无需依赖结构或材料的非线性效应，通过结合偏振和频率便能方便高效地实现多倍相位调制。由频率和偏振引起的多倍相位调制为使用单层超表面生成多倍相位提供了一种新颖的解决方案，可实现光方向激励与折射、轨道角动量光束转换及其他功能。与基于非线性效应的多相位调制相比，所开发的方法显著提高了能量转换效率，同时降低了实验复杂性。然而，由于所选结构范围有限，实现严格的数值多倍相位包络仍具有挑战性。可以通过扩展可用结构范围并选择实现固定相位元件的方法来解决这一问题。在匹配多路复用相位图时，优先考虑最小相位匹配误差。这在一定程度上忽略了振幅约束，导致不同通道光强的差异。通过调整算法重建的不同通道损失强度比，可以同时减少匹配的振幅和相位误差，从而选择最优相位结构。此外，通过精细设计，该算法可扩展为实现动态轨道角动量光束的定向激励与通信。鉴于这些独特优势，我们相信，本研究不仅增强了多倍相位调制的方法，还为定向光通信、光开关、全息加密与显示、动态光学调制及多个领域的发展奠定了基础。

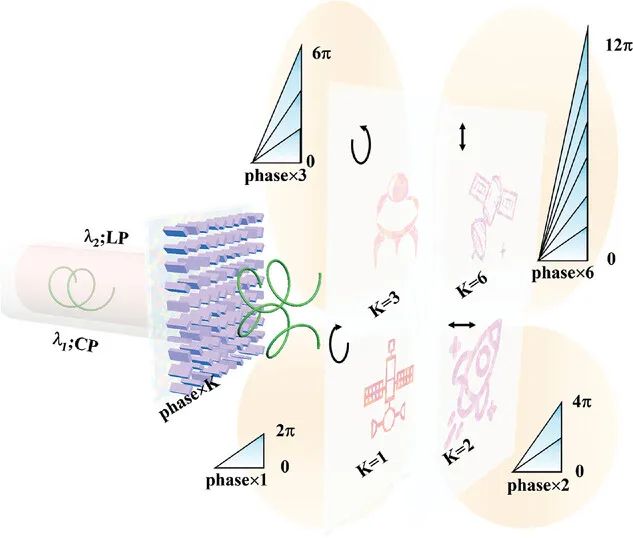
图1. 基于频率和偏振引发的多倍相位全息概念（LP：线偏振；CP：圆偏振；K：相位倍数）

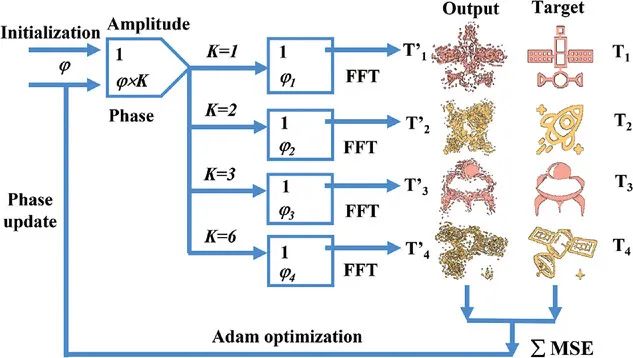
图2. 多倍相位全息算法原理

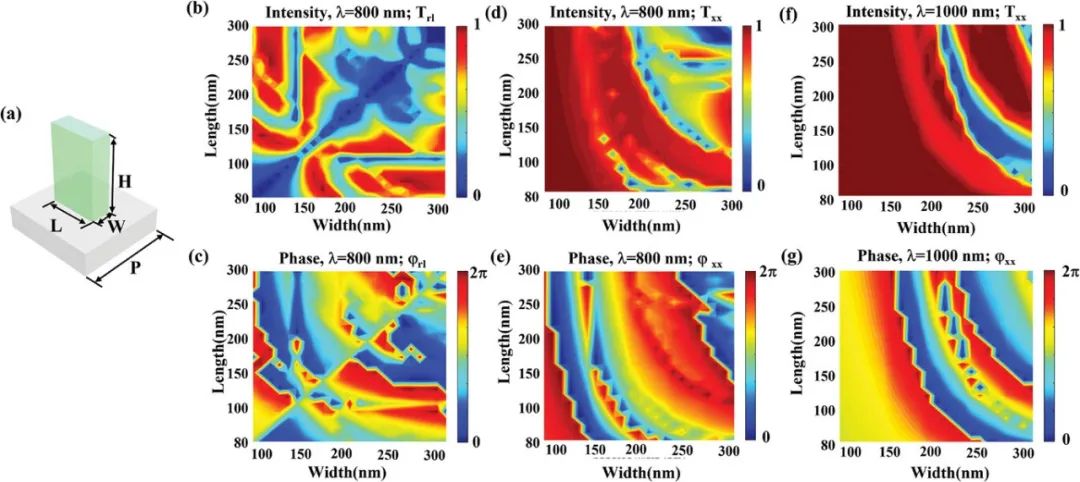
图3.纳米结构单元和透射图。
a) 纳米鳍的概念图（H：高度，W：宽度，L：长度，P：晶格常数）。
b, c) 在入射波长800 nm时的交叉圆偏振透射强度和相位图。
d, e) 在入射波长800 nm时的共线偏振透射强度和相位图，分别对长度和宽度进行扫描。
f, g) 在入射波长1000 nm时的共线偏振透射强度和相位图，分别对长度和宽度进行扫描。

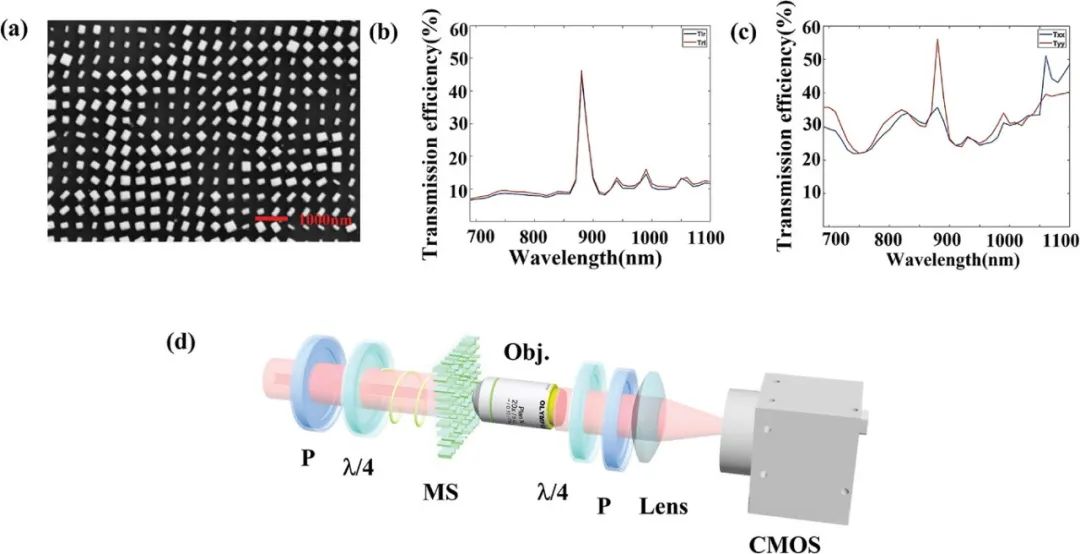
图4. 超表面样本和光学装置。

a) 超表面的扫描电子显微镜（SEM）图像（俯视图，比例尺：1000 nm）。

b) 在交叉圆偏振通道（Trl, Tlr）中的宽带透射效率曲线。

c) 在共线偏振通道（Txx, Tyy）中的宽带透射效率曲线。

d) 实验光学装置。（P：线偏振器；λ/4：四分之一波片；CMOS：互补金属氧化物半导体）。

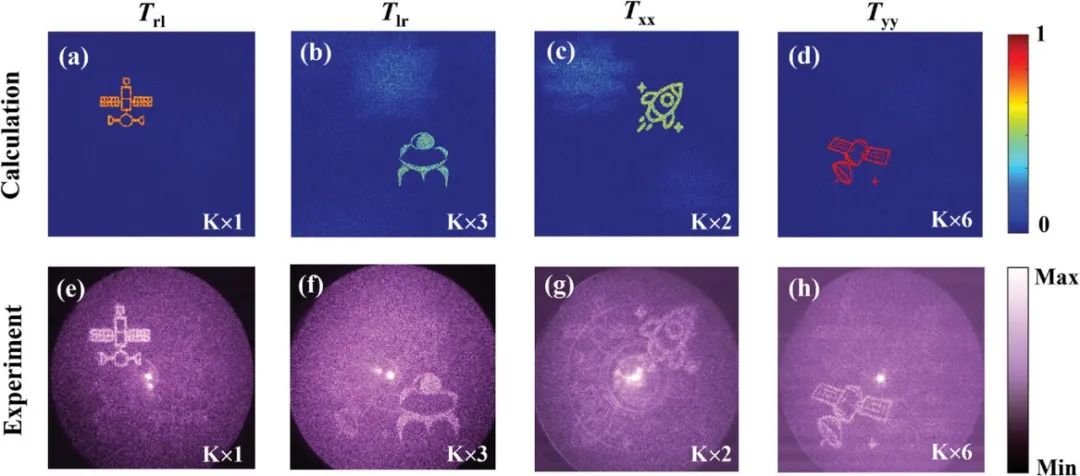
图5. 使用双波长和偏振获得的多倍相位全息的仿真和实验结果。
a, e) 在波长820 nm的交叉偏振（Trl）条件下，基本（K = 1）全息结果的计算和实验重建。
b, f) 在波长820 nm的交叉偏振（Tlr）条件下，多相位（K = 3）全息结果的计算和实验重建。
c, g) 在波长930 nm的共偏振（Txx）条件下，多相位（K = 2）全息结果的计算和实验重建。
d, h) 在波长930 nm的共偏振（Tyy）条件下，多相位（K = 6）全息结果的计算和实验重建。

H. Zhou, C. Zhao, C. He, Q. Jiang, H. Wang, R. Zhao, T. Man, Y. Wan, G. Geng, L. Huang, Multi-fold Phase Metasurface Holography Based on Frequency and Hybrid Decoupling Polarizations. Adv. Optical Mater. 2025, 2402303. 

DOI:https://doi.org/10.1002/adom.202402303