线性回归：梯度下降法 （包含三种梯度下降的python原代码，不是scikit learn 包）

梯度下降

梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。

假设你迷失在山上的浓雾之中，你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡。这就是梯度下降的做法：通过测量参数向量θ相关的误差函数的局部梯度，并不断沿着降低梯度的方向调整，直到梯度降为0，到达最小值！

具体来说，首先使用一个随机的θ值（这被称为随机初始化），然后逐步改进，每次踏出一步，每一步都尝试降低一点成本函数（如MSE），直到算法收敛出一个最小值

在梯度下降的描述中，模型参数被随机初始化并反复调整使成本函数最小化。学习步长与成本函数的斜率成正比，因此，当参数接近最小值时，步长逐渐变小

梯度下降中一个重要参数是每一步的步长，这取决于超参数学习率。如果学习率太低，算法需要经过大量迭代才能收敛，这将耗费很长时间。

反过来说，如果学习率太高，那你可能会越过山谷直接到达另一边，甚至有可能比之前的起点还要高。这会导致算法发散，值越来越大，最后无法找到好的解决方案

线性回归模型的MSE成本函数是个二次函数，所以连接曲线上任意两点的线段永远不会跟曲线相交。也就是说，不存在局部最小值，只有一个全局最小值。它同时也是一个连续函数，所以斜率不会产生陡峭的变化。这两点保证的结论是：即便是乱走，梯度下降都可以趋近到全局最小值（只要等待时间足够长，学习率也不是太高）

批量梯度下降

要实现梯度下降，你需要计算每个模型关于参数${\theta }_j$的成本函数的梯度。换言之，你需要计算的是如果只改变${\theta }_j$，成本函数会改变多少。这被称为偏导数。记作$$\frac{\partial }{\partial {\theta }_j}MSE(\theta )$$
成本函数的偏导数：参照二次函数求导$$\frac{\partial }{\partial {\theta }_j}MSE(\theta )=\frac{2}{m}\sum _{i=1}^m({\theta }^T{x}^{(i)}-y^{(i)})x_j^{(i)}$$

梯度向量记作$${\nabla }_{\theta }MSE(\theta )=\left(\begin{array}{c}\frac{\partial }{\partial {\theta }_0}MSE(\theta )\\ \frac{\partial }{\partial {\theta }_1}MSE(\theta )\\ \frac{\partial }{\partial {\theta }_2}MSE(\theta )\\ \dots \\ \frac{\partial }{\partial {\theta }_n}MSE(\theta )\end{array}\right)=\frac{2}{m}{X}^T({\theta }^{T}X-y)$$，包含所有成本函数（每个模型参数一个）的偏导数。

一旦有了梯度向量，哪个点向上，就朝反方向下坡。${\nabla }_{\theta }MSE(\theta )$。这时学习率$\eta$就发挥作用了：用梯度向量乘以$\eta$确定下坡步长的大小

公式：$$\theta =\theta -\eta {\nabla }_{\theta }MSE(\theta )$$

eta = 0.1 
n_iterations = 1000
m = 100

theta = np.random.randn(2,1) #initialization

for iteration in range(n_iterations):
	gradients = 2/m *X_b.T.dot(X_b.dot(theta)-y)
	theta = theta -eta*gradients

让我们看一下产生的theta：

theta

结果如下

array([[4.21509616],
       [2.77011339]])

来看看预测结果如何：

y_predict = X_new_b.dot(theta)
y_predict

结果如下

array([[4.21509616],
       [9.75532293]])

def plot_gradient_descent(theta ,eta):
	m = len(X_b)
	plt.plot(X,y,"b.")
	n_iterations = 1000
	for iteration in range(n_iterations):
		if iteration <10:
			y_predict = X_new_b.dot(theta)
			style = "b-" if iteration >0 else "r--" #第一次为红色 其余为蓝色
			plt.plot(X_new , y_predict ,style)
		gradients = 2/m*X_b.T.dot(X_b,dot(theta)-y)
		theta = theta - eta*gradients 
		
	plt.xlabel("$x_1$",fontsize = 18)
	plt.axis([0,2,0,15])
	plt.title(r"$\eta = {}$".format(eta),fontsize =16)

np.random.seed(42)
theta = np.random.randn(2,1)

plt.figure = (figsize = (10,4))
plt.subplot(131);plt_gradient_descent(theta ,eta = 0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132);plt_gradient_descent(theta ,eta = 0.1)
plt.subplot(133);plt_gradient_descent(theta ,eta = 0.5)

plt.savefig("gradient_descent_plot")
plt.show()

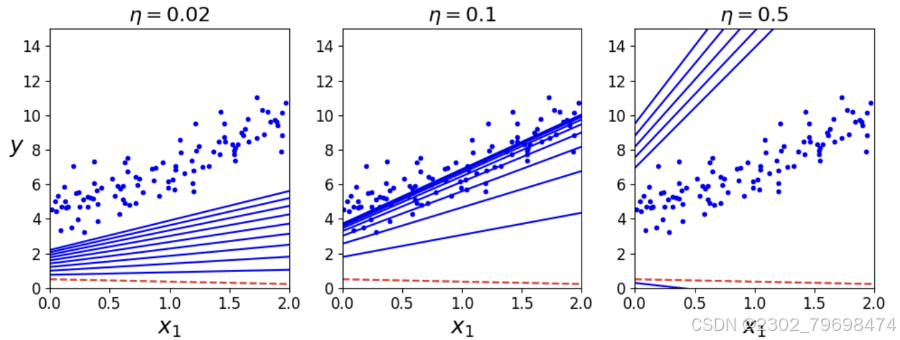
随机梯度下降 [随机序列求偏导]

批量梯度下降的主要问题是它要用整个训练集来计算每一步的梯度，所以训练集很大时，算法会特别慢。与之相反的极端是随机梯度下降，每一步在训练集中随机选择一个实例，并且仅基于该单个实例来计算梯度。显然，这让算法变得快多了，因为每次迭代都只需要操作少量的数据。它也可以被用来训练海量的数据集，因为每次迭代只需要在内存中运行一个实例即可。

另一方面，由于算法的随机性质，它比批量梯度下降要不规则得多。成本函数将不再是缓缓降低直到抵达最小值，而是不断上上下下，但是从整体来看，还是在慢慢下降。随着时间的推移，最终会非常接近最小值，但是即使它到达了最小值，依旧还会持续反弹，永远不会停止。所以算法停下来的参数值肯定是足够好的，但不是最优的。

代码实现：

n_epochs = 50
t0 ,t1 = 5,50 
def learning_schedule(t):
	returen t0 / (t+t1)

theta = np.random.randn(2,1)

for epoch in range(n_epochs):
	for i in range(m):
		random_index = np.random.randint(m) #随机序列求导
		xi = X_b[random_index:random_index+1]
		yi = y[random_index:random_index+1]
		gradients = 2*xi.T.dot(xi.dot(theta)-yi)
		eta = learning_schedule(epoch*m+i)
		theta = theta -eta*gradients

按照惯例，我们进行m个回合的迭代。每个回合称为一个轮次。

theta

结果如下

array([[4.21509296],
       [2.75615066]])

此代码仅在训练集中遍历了50次，并达到了一个很好的解决方案：

我们来看看图示

n_epochs = 50
t0, t1 = 5,50
def learning_schedule(t):
	return t0/(t+t1)
theta = np.random.randn(2,1)

for epoch in range(n_epochs):
    for i in range(m):
        if epoch ==0 and i<20:
            y_predict = X_new_b.dot(theta)
            style = "b-" if i>0 else "r--"
            plt.plot(X_new ,y_predict,style)
            
            
        random_index = np.random.randint(m)
        xi = X_b[random_index :random_index+1]
        yi = y[random_index :random_index+1]
        gradients =2*xi.T.dot(xi.dot(theta)-yi)
        eta = learning_schedule(epoch * m +i) #逐步减小
        theta = theta - eta*gradients
	
plt.plot(X,y,"b.")
plt.xlabel("$x_1$",fontsize = 18)
plt.ylabel("$y$",rotation=0,fontsize = 18)
plt.axis([0,2,0,15])
plt.savefig("sgd_plot")
plt.show()

结果如下：

请注意，由于实例是随机选取的，因此某些实例可能每个轮次中被选取几次，而其他实例则可能根本不被选取。如果要确保算法在每个轮次都遍历每个实例，则另一种方法是对训练集进行混洗（确保同时对输入特征和标签进行混洗），然后逐个实例进行遍历，然后对其进行再次混洗，以此类推。但是，这种方法通常收敛较慢。

要使用带有Scikit-Learn的随机梯度下降执行线性回归，可以使用SGDRegressor类，该类默认优化平方误差成本函数。以下代码最多可运行1000个轮次，或者直到一个轮次期间损失下降小于0.001为止（max_iter=1000，tol=1e-3）。它使用默认的学习调度（与前一个学习调度不同）以0.1（$et{a}_0=0.1$）的学习率开始。最后，它不使用任何正则化

from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000 , tol=1e-3,penalty = None ,eta=0.1)
sgd_reg.fit(X,y.ravel()) #将y平铺成一维数组

sgd_reg.intercept_
sgd_reg.coef_

结果如下：

(array([4.24365286]), array([2.8250878]))

小批量梯度下降

在每一步中，不是根据完整的训练集（如批量梯度下降）或仅基于一个实例（如随机梯度下降）来计算梯度，小批量梯度下降在称为小型批量的随机实例集上计算梯度。小批量梯度下降优于随机梯度下降的主要优点是，你可以通过矩阵操作的硬件优化来提高性能，特别是在使用GPU时。
代码实现

n_iterations = 50
minibatch_size = 20

np.random.seed(42)
theta = np.random.randn(2,1) #random initialization

t0 ,t1 = 200,1000
def learning_schedule(t):
	return t0 /(t+t1)

t= 0 
for epoch in range(n_iterations):
    shuffled_indices = np.random.permutation(m) #打乱
    X_b_shuffled = X_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for i in range(0,m,minibatch_size):
	    t += 1 # eta 递减
	    xi = X_b_shuffled[i:i+minibatch_size]
	    yi = y_shuffled[i:i+minibatch_size]
	    gradients = 2/minibatch_size*xi.T.dot(xi.dot(theta) - yi)
	    eta = learning_schedule(t)
	    theta = theta - eta*gradients
	    theta_path_mgd.append(theta)
print(theta)