一文详解 Diffusion 扩散模型：理论、架构与实现

最新推荐文章于 2025-04-14 13:56:28 发布

大模型与计算机视觉

最新推荐文章于 2025-04-14 13:56:28 发布

阅读量2k

点赞数 30

分类专栏：算法学习笔记文章标签：面试算法人工智能面试题多模态大模型扩散模型 AIGC

本文链接：https://blog.csdn.net/2401_84033492/article/details/143100670

版权

算法学习笔记专栏收录该内容

187 篇文章

订阅专栏

最近这一两周看到不少互联网公司都已经开始秋招发放Offer。

不同以往的是，当前职场环境已不再是那个双向奔赴时代了。求职者在变多，HC 在变少，岗位要求还更高了。

最近，我们又陆续整理了很多大厂的面试题，帮助一些球友解惑答疑，分享技术面试中的那些弯弯绕绕。

喜欢本文记得收藏、关注、点赞。更多实战和面试交流，文末加入我们

技术交流

在这里插入图片描述

本文深入探讨了Diffusion扩散模型的概念、架构设计与算法实现，详细解析了模型的前向与逆向过程、编码器与解码器的设计、网络结构与训练过程，结合PyTorch代码示例，提供全面的技术指导。

一、什么是Diffusion扩散模型？

Diffusion扩散模型是一类基于概率扩散过程的生成模型，近年来在生成图像、文本和其他数据类型方面展现出了巨大的潜力和优越性。该模型利用了扩散过程的逆过程，即从一个简单的分布逐步还原到复杂的数据分布，通过逐步去噪的方法生成高质量的数据样本。

1.1 扩散模型的基本概念

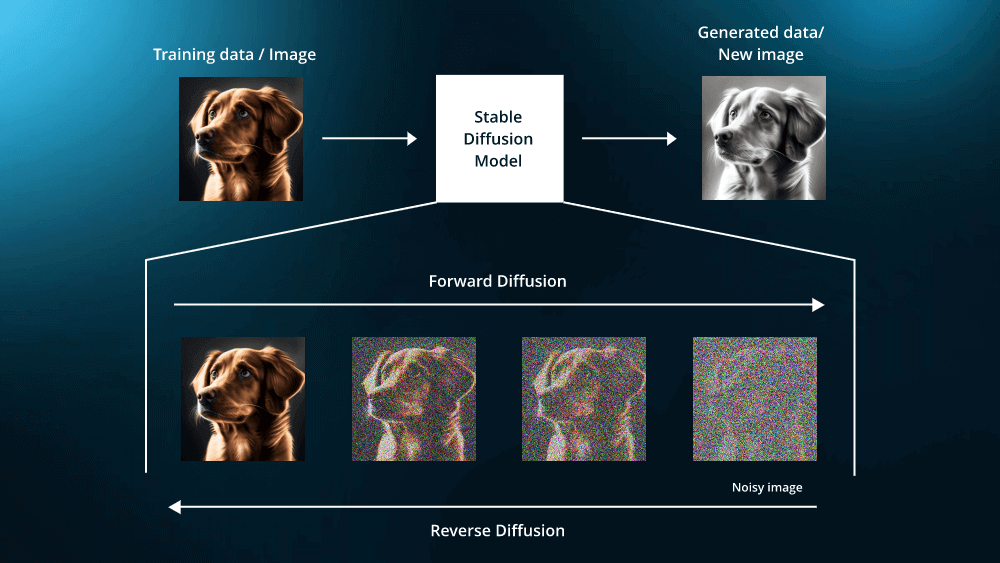
扩散模型的基本思想源于物理学中的扩散过程，这是一种自然现象，描述了粒子在介质中从高浓度区域向低浓度区域的移动。在机器学习中，扩散模型通过引入随机噪声逐步将数据转变为噪声分布，然后通过逆过程从噪声中逐步还原数据。具体来说，扩散模型包含两个主要过程：

1.2 数学基础

随机过程与布朗运动

热力学与扩散方程

1.3 扩散模型的主要类型

Denoising Diffusion Probabilistic Models (DDPMs)

DDPMs 是一种最具代表性的扩散模型，通过逐步去噪的方法实现数据生成。其主要思想是在前向过程添加高斯噪声，使数据逐步接近标准正态分布，然后通过学习逆过程逐步去噪，还原数据。DDPMs 的生成过程如下：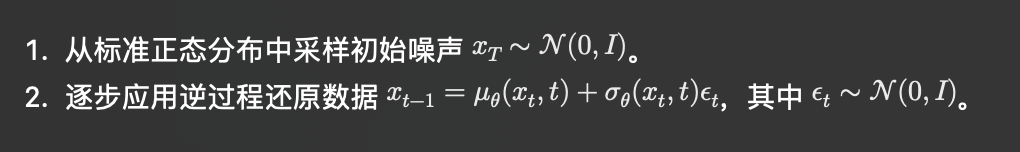

Score-Based Generative Models

1.4 扩散模型的优势与挑战

优势

高质量数据生成：扩散模型通过逐步去噪的方式生成数据，能够生成质量较高且逼真的样本。
稳定的训练过程：相比于 GANs（生成对抗网络），扩散模型的训练更加稳定，不易出现模式崩塌等问题。

挑战

计算复杂度高：扩散模型需要多步迭代过程，计算成本较高，训练时间较长。
模型优化难度大：逆过程的学习需要高效的优化算法，且对参数设置较为敏感。

1.5 应用实例

扩散模型已经在多个领域得到了广泛应用，如图像生成与修复、文本生成与翻译、医疗影像处理和金融数据生成等。以下是一些具体应用实例：

图像生成与修复：通过扩散模型可以生成高质量的图像，修复损坏或有噪声的图像。
文本生成与翻译：结合生成式预训练模型，扩散模型在自然语言处理领域展现出强大的生成能力。
医疗影像处理：扩散模型用于去噪、超分辨率等任务，提高医疗影像的质量和诊断准确性。

二、模型架构

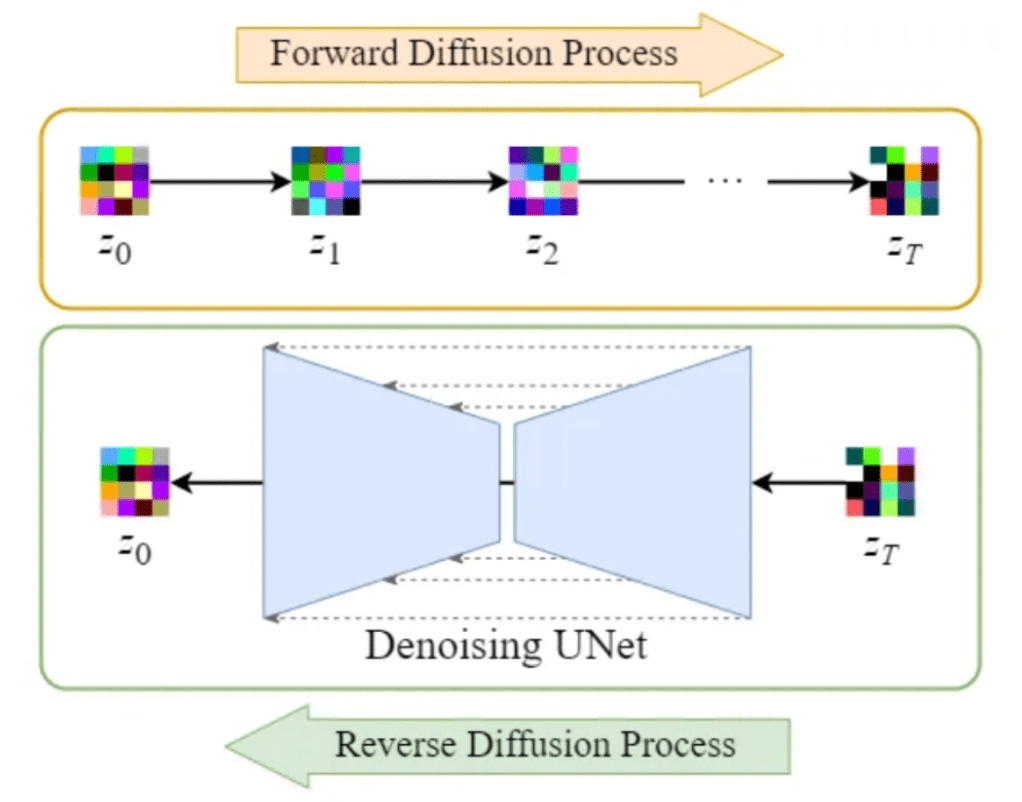
在理解了Diffusion扩散模型的基本概念后，我们接下来深入探讨其模型架构。Diffusion模型的架构设计直接影响其性能和生成效果，因此需要详细了解其各个组成部分，包括前向过程、逆向过程、关键参数、超参数设置以及训练过程。

2.1 前向过程

前向过程，也称为扩散过程，是Diffusion模型的基础。该过程逐步将原始数据添加噪声，最终转换为标准正态分布。具体步骤如下：

2.1.1 噪声添加

2.1.2 时间步长选择

时间步长 (T) 的选择对模型性能至关重要。较大的 (T) 值可以使噪声添加过程更加平滑，但也会增加计算复杂度。通常，(T) 的取值在1000至5000之间。

2.2 逆向过程

逆向过程是Diffusion模型生成数据的关键。该过程从标准正态分布开始，逐步去噪，最终还原原始数据。逆向过程的目标是学习条件概率分布 (p(x_{t-1} | x_t))，具体步骤如下：

2.2.1 学习逆过程

2.2.2 网络结构

通常，逆向过程使用U-Net或Transformer结构来实现，其网络架构包括多个卷积层或自注意力层，以捕捉数据的多尺度特征。具体的网络结构设计取决于具体的应用场景和数据类型。

2.3 关键参数与超参数设置

Diffusion模型的性能高度依赖于参数和超参数的设置，以下是一些关键参数和超参数的详细说明：

2.3.1 噪声比例参数 (\beta_t)

噪声比例参数 (\beta_t) 控制前向过程中添加的噪声量。通常，(\beta_t) 会随着时间步长 (t) 的增加而增大，可以采用线性或非线性递增策略。

2.3.2 时间步长 (T)

时间步长 (T) 决定了前向和逆向过程的步数。较大的 (T) 值可以使模型更好地拟合数据分布，但也会增加计算开销。

2.3.3 学习率

学习率是优化算法中的一个重要参数，控制模型参数更新的速度。较高的学习率可以加快训练过程，但可能导致不稳定，较低的学习率则可能导致收敛速度过慢。

2.4 训练过程详解

2.4.1 训练数据准备

在训练Diffusion模型之前，需要准备高质量的训练数据。数据应尽可能涵盖目标分布的各个方面，以提高模型的泛化能力。

2.4.2 损失函数设计

2.4.3 优化算法

Diffusion模型通常使用基于梯度的优化算法进行训练，如Adam或SGD。优化算法的选择和超参数的设置会显著影响模型的收敛速度和生成效果。

2.4.4 模型评估

模型评估是Diffusion模型开发过程中的重要环节。常用的评估指标包括生成数据的质量、与真实数据的分布差异等。以下是一些常用的评估方法：

定量评估：使用指标如FID（Frechet Inception Distance）、IS（Inception Score）等衡量生成数据与真实数据的相似度。
定性评估：通过人工评审或视觉检查生成数据的质量。

三、算法实现

在了解了Diffusion扩散模型的架构设计后，接下来我们将详细探讨其具体的算法实现。本文将以PyTorch为例，深入解析Diffusion模型的代码实现，包括编码器与解码器设计、网络结构与层次细节，并提供详细的代码示例与解释。

3.1 编码器与解码器设计

Diffusion模型的核心在于编码器和解码器的设计。编码器负责将数据逐步转化为噪声，而解码器则负责逆向过程，从噪声还原数据。下面我们详细介绍这两个部分。

3.1.1 编码器

编码器的设计目标是通过前向过程将原始数据逐步转化为噪声。典型的编码器由多个卷积层组成，每一层都会在数据上添加一定量的噪声，使其逐步接近标准正态分布。

import torch
import torch.nn as nn

class Encoder(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers):
        super(Encoder, self).__init__()
        self.layers = nn.ModuleList()
        for i in range(num_layers):
            in_dim = input_dim if i == 0 else hidden_dim
            self.layers.append(nn.Conv2d(in_dim, hidden_dim, kernel_size=3, stride=1, padding=1))
            self.layers.append(nn.BatchNorm2d(hidden_dim))
            self.layers.append(nn.ReLU())

    def forward(self, x):
        for layer in self.layers:
            x = layer(x)
        return x

3.1.2 解码器

解码器的设计目标是通过逆向过程从噪声还原原始数据。典型的解码器也由多个卷积层组成，每一层逐步去除数据中的噪声，最终还原出高质量的数据。

class Decoder(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers):
        super(Decoder, self).__init__()
        self.layers = nn.ModuleList()
        for i in range(num_layers):
            in_dim = input_dim if i == 0 else hidden_dim
            self.layers.append(nn.Conv2d(in_dim, hidden_dim, kernel_size=3, stride=1, padding=1))
            self.layers.append(nn.BatchNorm2d(hidden_dim))
            self.layers.append(nn.ReLU())
        self.final_layer = nn.Conv2d(hidden_dim, 3, kernel_size=3, stride=1, padding=1)

    def forward(self, x):
        for layer in self.layers:
            x = layer(x)
        x = self.final_layer(x)
        return x

3.2 网络结构与层次细节

Diffusion模型的整体网络结构通常采用U-Net或类似的多尺度网络，以捕捉数据的不同层次特征。下面我们以U-Net为例，详细介绍其网络结构和层次细节。

3.2.1 U-Net架构

U-Net是一种典型的用于图像生成和分割任务的网络架构，其特点是具有对称的编码器和解码器结构，以及跨层的跳跃连接。以下是U-Net的实现：

class UNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers):
        super(UNet, self).__init__()
        self.encoder = Encoder(input_dim, hidden_dim, num_layers)
        self.decoder = Decoder(hidden_dim, hidden_dim, num_layers)

    def forward(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return decoded

3.2.2 跳跃连接

跳跃连接（skip connections）是U-Net架构的一大特色，它可以将编码器各层的特征直接传递给解码器对应层，从而保留更多的原始信息。以下是加入跳跃连接的U-Net实现：

class UNetWithSkipConnections(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers):
        super(UNetWithSkipConnections, self).__init__()
        self.encoder = Encoder(input_dim, hidden_dim, num_layers)
        self.decoder = Decoder(hidden_dim * 2, hidden_dim, num_layers)

    def forward(self, x):
        skips = []
        for layer in self.encoder.layers:
            x = layer(x)
            if isinstance(layer, nn.ReLU):
                skips.append(x)

        skips = skips[::-1]
        for i, layer in enumerate(self.decoder.layers):
            if i % 3 == 0 and i // 3 < len(skips):
                x = torch.cat((x, skips[i // 3]), dim=1)
            x = layer(x)

        x = self.decoder.final_layer(x)
        return x

3.3 代码示例与详解

3.3.1 完整模型实现

结合前面的编码器、解码器和U-Net架构，我们可以构建一个完整的Diffusion模型。以下是完整模型的实现：

class DiffusionModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, num_layers):
        super(DiffusionModel, self).__init__()
        self.unet = UNetWithSkipConnections(input_dim, hidden_dim, num_layers)

    def forward(self, x):
        return self.unet(x)

# 模型实例化
input_dim = 3  # 输入图像的通道数
hidden_dim = 64  # 隐藏层特征图的通道数
num_layers = 4  # 网络层数
model = DiffusionModel(input_dim, hidden_dim, num_layers)

3.3.2 训练过程

为了训练Diffusion模型，我们需要定义训练数据、损失函数和优化器。以下是一个简单的训练循环示例：

import torch.optim as optim

# 数据加载（假设我们有一个DataLoader对象dataloader）
dataloader = ...

# 损失函数
criterion = nn.MSELoss()

# 优化器
optimizer = optim.Adam(model.parameters(), lr=1e-4)

# 训练循环
num_epochs = 100
for epoch in range(num_epochs):
    for i, data in enumerate(dataloader):
        inputs, targets = data
        inputs, targets = inputs.to(device), targets.to(device)

        # 前向传播
        outputs = model(inputs)

        # 计算损失
        loss = criterion(outputs, targets)

        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if i % 100 == 0:
            print(f"Epoch [{epoch}/{num_epochs}], Step [{i}], Loss: {loss.item():.4f}")

3.3.3 生成数据

训练完成后，我们可以使用模型生成数据。以下是一个简单的生成过程示例：

# 生成过程
def generate(model, num_samples, device):
    model.eval()
    samples = []
    with torch.no_grad():
        for _ in range(num_samples):
            noise = torch.randn(1, 3, 64, 64).to(device)
            sample = model(noise)
            samples.append(sample.cpu())
    return samples

# 生成样本
num_samples = 10
samples = generate(model, num_samples, device)

通过以上详细的算法实现说明和代码示例，我们可以清晰地看到Diffusion模型的具体实现过程。通过合理设计编码器、解码器和网络结构，并结合有效的训练策略，Diffusion模型能够生成高质量的数据样本。