动手学运动规划: 2.4 3次螺旋线(Cubic Spiral Curve)

自动驾驶小白说

于 2024-10-09 09:00:00 发布

阅读量885

点赞数 12

分类专栏：动手学运动规划文章标签：自动驾驶算法运动规划

本文链接：https://blog.csdn.net/2403_86993842/article/details/142770497

版权

动手学运动规划专栏收录该内容

20 篇文章 0 订阅

订阅专栏

应是天仙狂醉，乱把白云揉碎。— 唐李白

🏰代码及环境配置：请参考环境配置和代码运行!

之前介绍的曲线形式, 都是基于参数方程构造的. 这种方法有一个共同的缺点: 对于曲线上的弧长, 曲率, 计算比较困难.

$\kappa=\frac{y^{\prime \prime} x^{\prime}-x^{\prime \prime} y^{\prime}}{\left(x^{\prime 2}+y^{\prime 2}\right)^{\frac{2}{3}}}$

正如上式, 他们需要1阶,2阶导数才能得到曲率信息, 需要做大量的求根运算才能得到弧长. 这毫无疑问需要较大的计算资源. 那么如果某些情况下, 我们会大量的用到曲率和弧长, 有没有办法能够方便的得到呢?

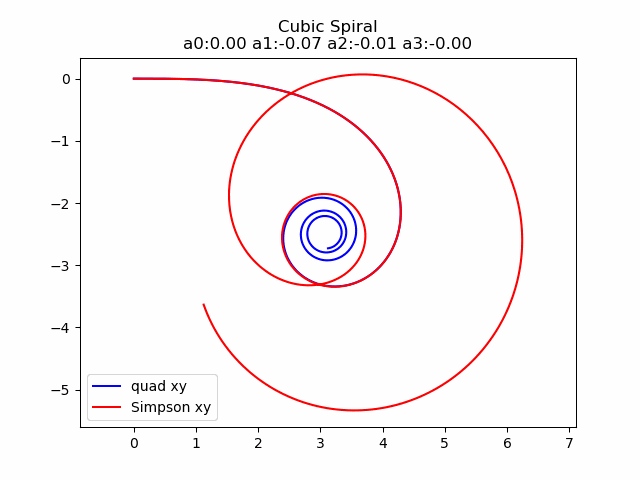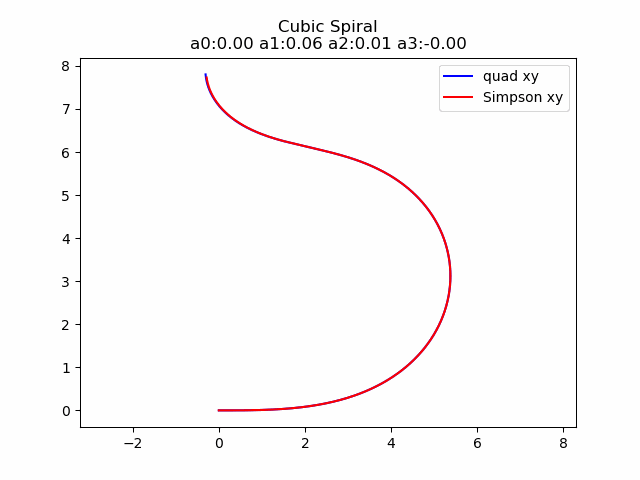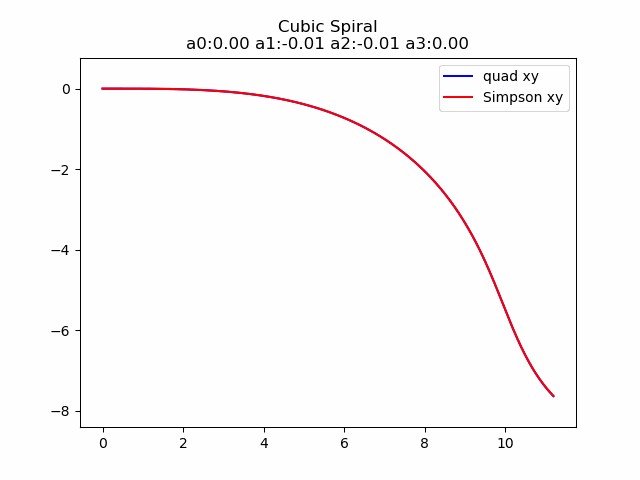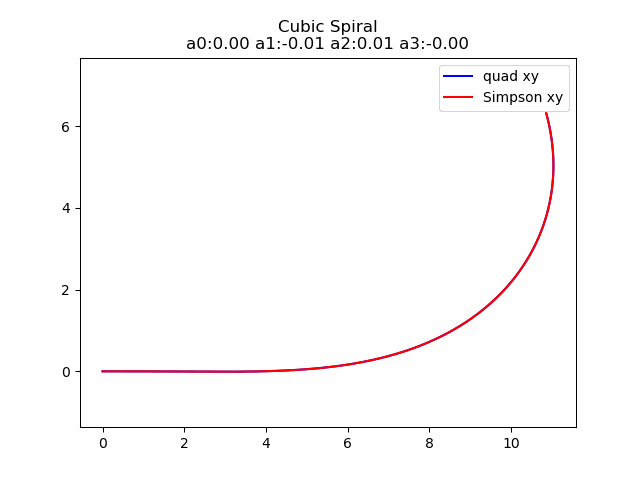
2.4.1 3次螺旋线定义

3次螺旋线就是这样一种方法, 它是由一个曲率 $k$ 关于弧长 $s$ 的多项式定义的.

$\kappa(s)=a_3 s^3+a_2 s^2+a_1 s+a_0$

$a_0, a_1, a_2, a_3$ 是参数, 这样我们可以直接使用弧长s简单的计算曲率 $k$ .

但是对应的, 计算x, y会变的很麻烦, 需要使用积分. (这就是人生啊~)

假设我们有一个用3次螺旋线表达的曲线, 它的始末状态分别是 $(x_0,y_0, \theta_0, k_0),(x_f,y_f, \theta_f, k_f)$ .

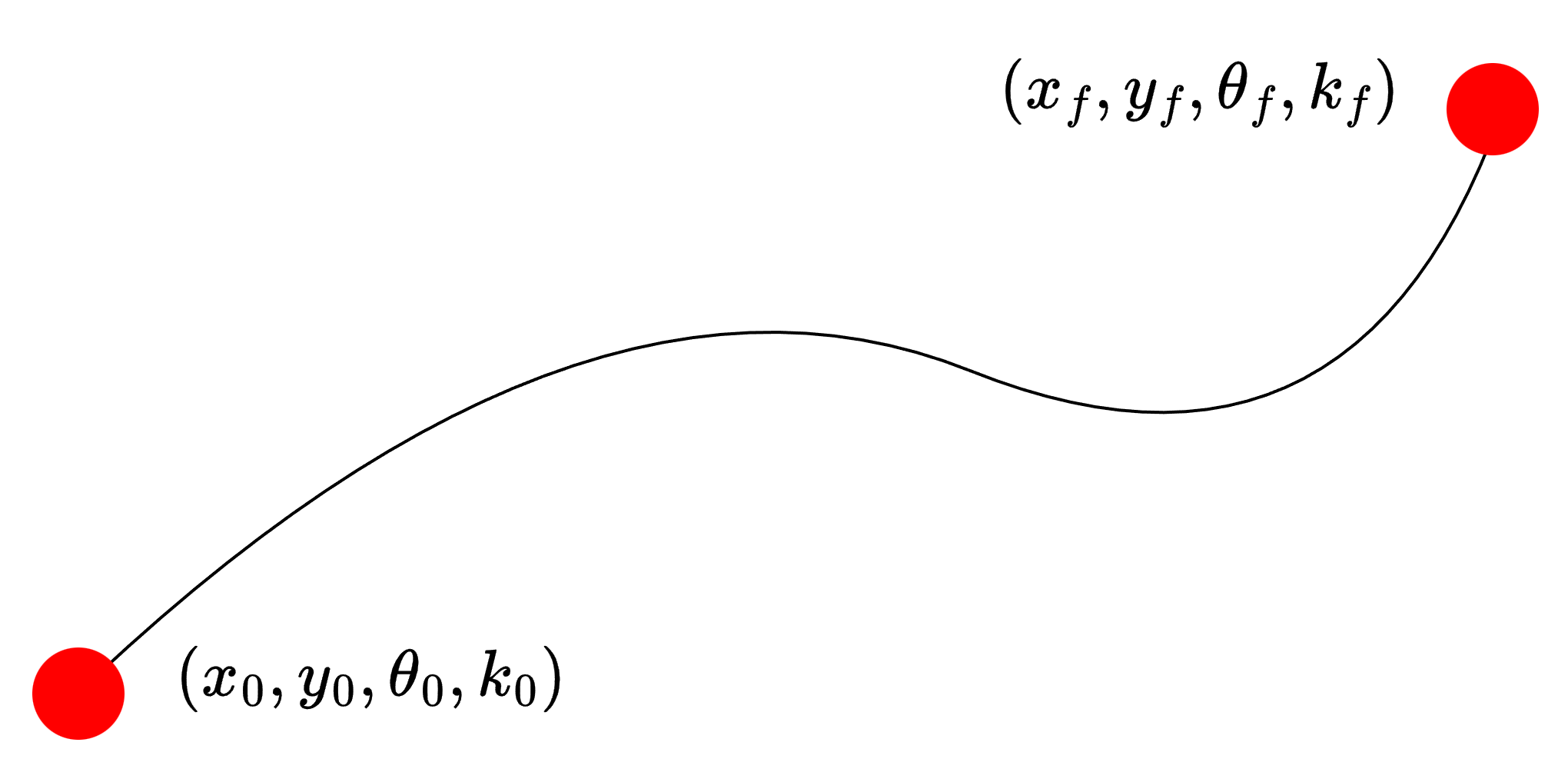
曲率=切向角的变化率/弧长的变化率. 因此从起始点开始对曲率进行积分可以得到切向角. 很容易可以得到切向角 $\theta(s)$ 的表达式

$\kappa = \frac{d\theta}{ds}$

$\begin{aligned}\theta(s) & =\theta_0+\int_0^s a_3 s^{\prime 3}+a_2 s^{\prime 2}+a_1 s^{\prime}+a_0 d s^{\prime} \\& =\theta_0+a_3 \frac{s^4}{4}+a_2 \frac{s^3}{3}+a_1 \frac{s^2}{2}+a_0 s\end{aligned}$

接下来我们再计算x,y, 需要通过 $\theta$ 积分得到:

$\begin{aligned}& x(s)=x_0+\int_0^s \cos \left(\theta\left(s^{\prime}\right)\right) d s^{\prime} \\& y(s)=y_0+\int_0^s \sin \left(\theta\left(s^{\prime}\right)\right) d s^{\prime}\end{aligned}$

这样我们有了 $\theta, k)$ 的完整表达, 但是似乎没有解决问题, 因为积分运算 $\int_0^s \cos \left(\theta\left(s^{\prime}\right)\right) d s^{\prime}$ 岂不是更复杂?

是的, 我们很难去算这个积分, 但是我们可以求积分的近似值.

2.4.2 辛普森法则(Simpson’s Rule)

辛普森法则（Simpson’s Rule）是一种数值积分方法，用于近似计算定积分的值。它是基于插值多项式的数值积分方法中的一种，特别地，它使用了二次多项式（抛物线）来逼近被积函数在小区间上的行为。下图的蓝线 $f (x)$ 是原曲线, 红线 $P (x)$ 是逼近的曲线.

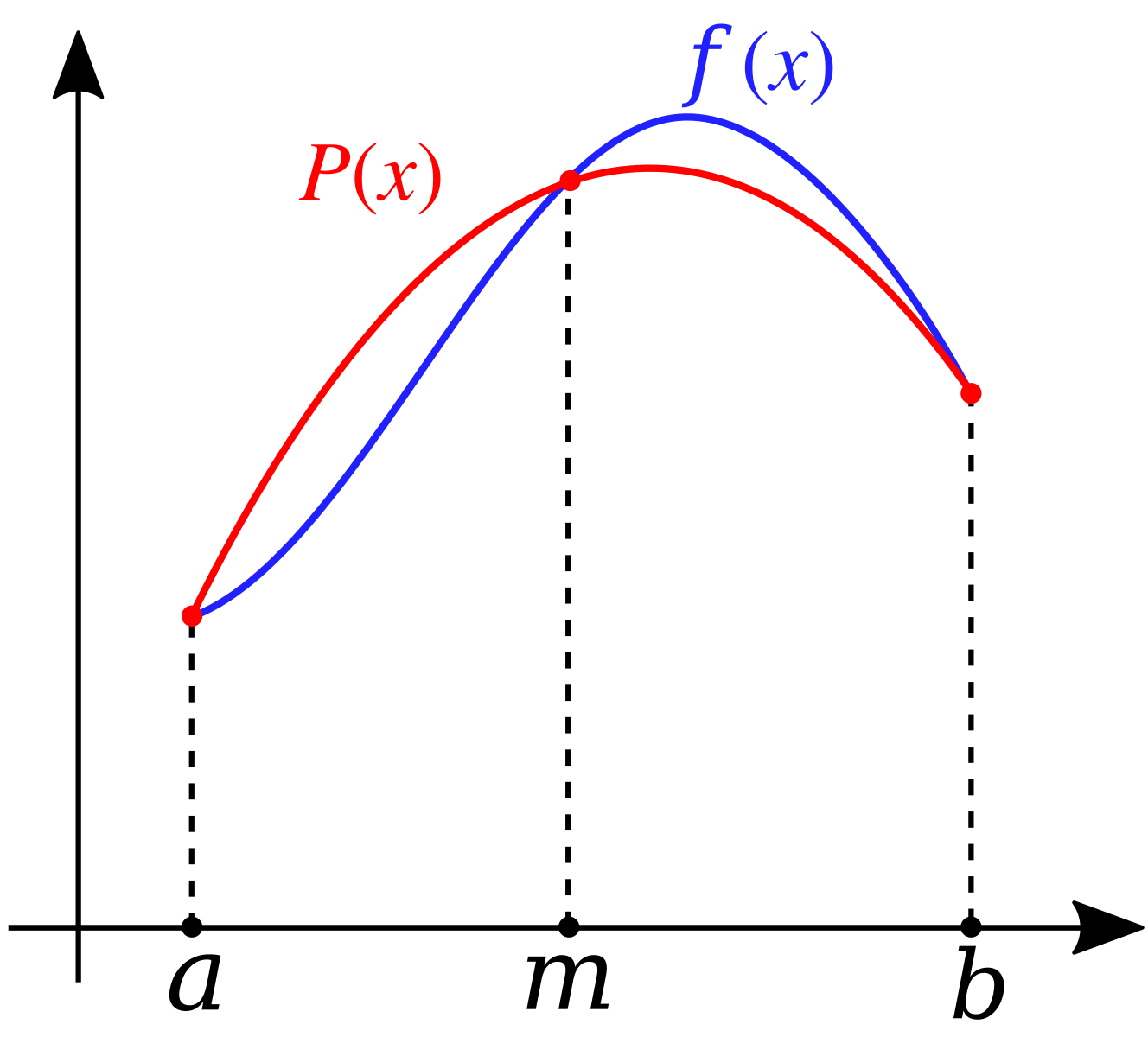
该法则通过将积分区间[a,b]等分为n个小区间（n为偶数），然后在每个小区间内选取三个点（例如，第i个小区间的点 $x_i, x_{i+1}, x_{i+2}$ ），利用这三个点构造一条抛物线，以此抛物线的积分值来近似表示该小区间内被积函数的积分值。最终，将所有小区间的积分值相加，得到整个积分区间的近似积分值。

这个动图能够更加直观的解释这个过程, 每3个点构造一个二次多项式, 然后对二次多形式积分.

$\Delta x$ 表示采样点的间距, 可以明显看出来采样点越密集, 整体误差越小. 当然相对的, 计算量越大.

辛普森法则的计算公式有多种形式，其中较为常见的是辛普森1/3法则和辛普森3/8法则。我们使用辛普森1/3法则：

$\int_0^s f\left(s^{\prime}\right) d s^{\prime} \approx \frac{s}{3 n}\left(f(0)+4 f\left(\frac{s}{n}\right)+2 f\left(\frac{2 s}{n}\right)+\cdots+f(s)\right)$

$n$ 代表在区间内切割成多少份. 我们设定 $n = 8$ , 将辛普森法则应用到 $\theta)$ 的积分中, 得到积分的近似解.

$\begin{aligned}x(s)\approx x_0+\frac{s}{24}[\cos (\theta(0)) & +4 \cos \left(\theta\left(\frac{s}{8}\right)\right)+2 \cos \left(\theta\left(\frac{2 s}{8}\right)\right)+4 \cos \left(\theta\left(\frac{3 s}{8}\right)\right)+2 \cos \left(\theta\left(\frac{4 s}{8}\right)\right) \\& \left.+4 \cos \left(\theta\left(\frac{5 s}{8}\right)\right)+2 \cos \left(\theta\left(\frac{6 s}{8}\right)\right)+4 \cos \left(\theta\left(\frac{7 s}{8}\right)\right)+\cos (\theta(s))\right] \\y(s)\approx y_0+\frac{s}{24}[\sin (\theta(0)) & +4 \sin \left(\theta\left(\frac{s}{8}\right)\right)+2 \sin \left(\theta\left(\frac{2 s}{8}\right)\right)+4 \sin \left(\theta\left(\frac{3 s}{8}\right)\right)+2 \sin \left(\theta\left(\frac{4 s}{8}\right)\right) \\& \left.+4 \sin \left(\theta\left(\frac{5 s}{8}\right)\right)+2 \sin \left(\theta\left(\frac{6 s}{8}\right)\right)+4 \sin \left(\theta\left(\frac{7 s}{8}\right)\right)+\sin (\theta(s))\right]\end{aligned}$