醉后不知天在水,满船清梦压星河。— 唐温如
🏰代码及环境配置:请参考0.2 环境配置和代码运行 | 动手学运动规划!
本节提供了基于5次多项式的参数方程曲线的代码测试
python3 tests/curves/quintic_polynomial.py
2.1.c.1 基于5次多项式的参数方程代码实现
在tests/curves/quintic_polynomial.py 我们定义了QuinticPolynomial , 它实现了5次多项式的参数方程的参数求解.
class QuinticPolynomial:
def __init__(self, xs, vxs, axs, xe, vxe, axe, time):
# calc coefficient of quintic polynomial
# See jupyter notebook document for derivation of this equation.
self.a0 = xs
self.a1 = vxs
self.a2 = axs / 2.0
A = np.array(
[
[time**3, time**4, time**5],
[3 * time**2, 4 * time**3, 5 * time**4],
[6 * time, 12 * time**2, 20 * time**3],
]
)
b = np.array(
[
xe - self.a0 - self.a1 * time - self.a2 * time**2,
vxe - self.a1 - 2 * self.a2 * time,
axe - 2 * self.a2,
]
)
x = np.linalg.solve(A, b)
self.a3 = x[0]
self.a4 = x[1]
self.a5 = x[2]
我们需要给出多项式在起点和终点的状态约束: x s , v s , a s x_s,v_s,a_s xs,vs,as和 x e , v e , a e x_e,v_e,a_e xe,ve,ae, 求解过程上一节解释过.
求解之后, QuinticPolynomial提供了相关接口来计算5次多项式的0阶, 1阶, 2阶导数:
def calc_point(self, t):
xt = (
self.a0
+ self.a1 * t
+ self.a2 * t**2
+ self.a3 * t**3
+ self.a4 * t**4
+ self.a5 * t**5
)
return xt
def calc_first_derivative(self, t):
xt = (
self.a1
+ 2 * self.a2 * t
+ 3 * self.a3 * t**2
+ 4 * self.a4 * t**3
+ 5 * self.a5 * t**4
)
return xt
def calc_second_derivative(self, t):
xt = 2 * self.a2 + 6 * self.a3 * t + 12 * self.a4 * t**2 + 20 * self.a5 * t**3
return xt
def calc_third_derivative(self, t):
xt = 6 * self.a3 + 24 * self.a4 * t + 60 * self.a5 * t**2
return xt
2.1.c.2 基于5次多项式的参数方程曲线代码测试
在main函数中, 我们给出多项式在起点和终点的状态约束:
x
s
,
v
s
,
a
s
x_s,v_s,a_s
xs,vs,as和
x
e
,
v
e
,
a
e
x_e,v_e,a_e
xe,ve,ae. 调用了quintic_polynomials_planner , 它求解了x,y的参数方程, 并将参数方程的结果插值提取出来用于可视化.
正如上节所述,因为无法确定曲线结果是否有效, 所以这里采取了对总时间T采样的方式, 寻找是否存在有效轨迹.
def quintic_polynomials_planner(
sx, sy, syaw, sv, sa, gx, gy, gyaw, gv, ga, max_accel, max_jerk, dt
):
for T in np.arange(MIN_T, MAX_T, MIN_T):
xqp = QuinticPolynomial(sx, vxs, axs, gx, vxg, axg, T)
yqp = QuinticPolynomial(sy, vys, ays, gy, vyg, ayg, T)
for t in np.arange(0.0, T + dt, dt):
...
ax = xqp.calc_second_derivative(t)
ay = yqp.calc_second_derivative(t)
a = np.hypot(ax, ay)
if len(rv) >= 2 and rv[-1] - rv[-2] < 0.0:
a *= -1
ra.append(a)
jx = xqp.calc_third_derivative(t)
jy = yqp.calc_third_derivative(t)
j = np.hypot(jx, jy)
if len(ra) >= 2 and ra[-1] - ra[-2] < 0.0:
j *= -1
rj.append(j)
if (
max([abs(i) for i in ra]) <= max_accel
and max([abs(i) for i in rj]) <= max_jerk
):
print("find path!!")
break
只要曲线上的每一个点, 都满足最大加速度约束:max_accel 和最大加加速度约束:max_jerk , 即认为曲线有效.
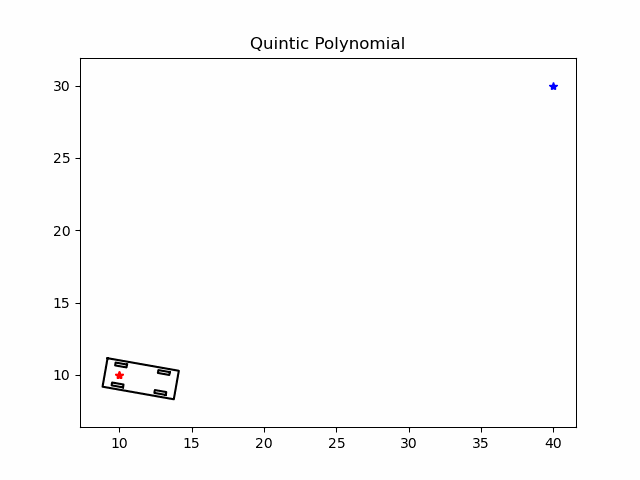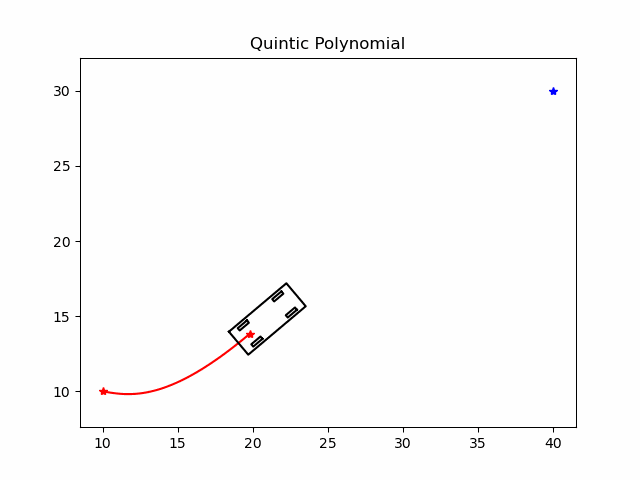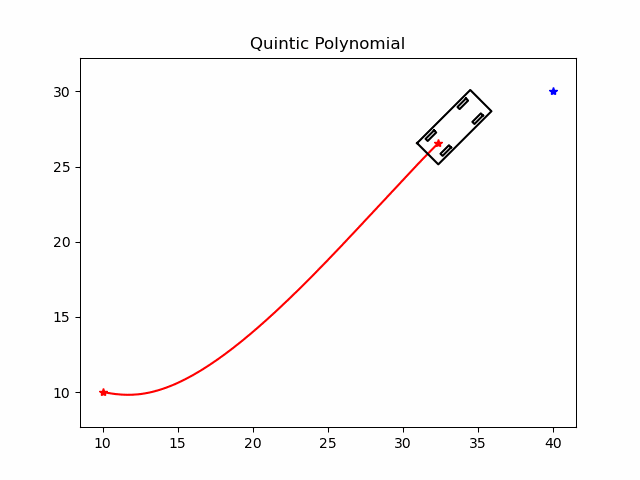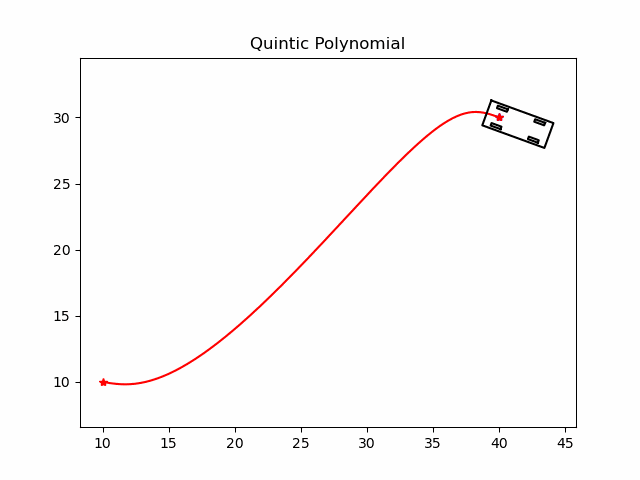
🏎️自动驾驶小白说官网:https://www.helloxiaobai.cn
🐮GitHub代码仓:https://github.com/Hello-Xiao-Bai/Planning-XiaoBai!
🔥课程答疑,面试辅导:https://shop380995420.taobao.com
🌠代码配合官网教程食用更佳!
🚀知乎,微信,知识星球全平台同号!























 6057
6057

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








