【重读经典】轨迹预测迈向工业落地第一文:VectorNet

VectorNet是在2020年由Waymo提出的轨迹预测网络.它的矢量化场景表征方法极大的提高了模型的性能和效率,直至今天仍然是主流的表征方法,可谓是轨迹预测迈向工业落地的里程碑论文.本文将重新梳理VectorNet.

主要贡献

1. 第一个矢量化场景上下文和智能体的动力学信息进行行为预测。
2. 我们提出了分层图网络以及节点完成辅助任务。
3. 在内部行为预测数据集和Argoverse数据集上评估了此方法，与渲染的方法相比达到了同等或更好的性能，并节省了70%的模型尺寸。这个方法在Argoverse上也达到了最优的性能。

VectorNet 模型

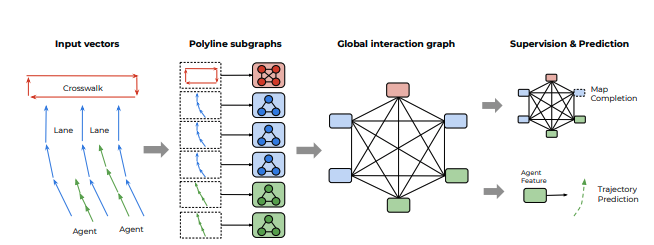
我们提出的矢量网概述。观察到的智能体轨迹和地图特征被表示为向量序列，并传递到局部图形网络以获得多段线级特征。然后将这些特征传递到完全连通的图模型高阶相互作用。我们计算了两种类型的损失：根据智能体对应于节点特征预测未来的轨迹以及其特征被掩盖时预测节点特征。

1.轨迹和地图的表示

HD地图中的大多数表示都是样条曲线（如车道）、闭合形状（如交叉口区域）和点（如红绿灯），以及附加属性信息，如当前状态（如交通颜色，道路速度限制）。对于智能体，其轨迹是关于时间的有向样条曲线形式。所有这些元素都可以近似为矢量序列。

对于地图特征，我们选择一个起点和方向，从条线中均匀采样关键点并将相邻的关键点依次连接成向量；对于轨迹，我们可以从t=0开始，以固定的时间间隔（0.1秒）采样关键点，并将它们连接到向量中。给定足够小的空间或时间间隔，生成的多段线可作为地图和轨迹的近似值。

我们的矢量化过程是连续轨迹和vector set、地图信息和vector set之间的一对一映射，尽管后者是无序的。这允许我们可以通过图神经网络进行编码。更具体地说，我们将属于多段线$P_j$的每个向量$v_i$视为图中的node，其node表示为

v i = { d i s , d i e , a i , j } v_{i} = \left\{ d_{i}^{s},d_{i}^{e},a_{i},j \right\} vi​={dis​,die​,ai​,j}

$d_i^s,d_i^e$前两个 是起点和终点的坐标,$a_i$对应于属性特征，如对象类型、轨迹的时间戳或车道的道路特征类型或速度限制；j 是$P_j$的整数id，表示$v_i$∈ $P_j$。

归一化：为了使输入节点特征相对位置不变,对于目标智能体，作者以目标智能体最后的观测时间下的位置，对所有向量的坐标进行归一化。

2.构造多段线子图

为了利用节点的空间和语义局部性，这里采用分层方法，首先在向量层构造子图，其中所有向量节点都相互连接，并且用同一多段线表示。考虑具有节点{$v_1，v_2，\dots ，v_P$}的多段线P将单层子图传播操作定义为：

$$v_i^{(l+1)}={\phi }_{rel}(genc(v_i^{(l)}),{\phi }_{agg}(genc(v_j^{(l)}))$$

其中 $v_i^{(l)}$ 是l层子网络上面的节点特征， $v_l^0$ 是输入特征 vi 。

$genc(.)$ 用于转换独立的节点，是一个MLP,所有节点共享参数。一层全连接层后面跟着layer normalization 和ReLU non-linearity。

${\phi }_{agg(.)}$用于集合周边节点的信息，是一个最大池化的操作。

${\phi }_{rel(.)}$ 表示节点和其邻居之间的关系，是一个简单的连接运算。

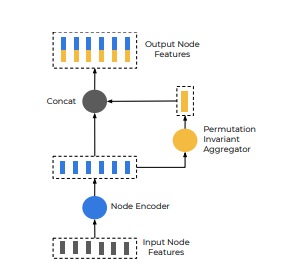
相同多线段下节点的计算流

我们堆叠多层子图网络，其中$genc(.)$的权重不同。最后，为了获得polyline级别的特征上，我们计算

$$⁍$$

其中$genc(.)$再一次最大池化。

3.高阶交互的全局图

我们现在在全局交互图中考虑polyline node之间的交互，用全局交互图进行建模：

$$\left\{p_i^{\left(l+1\right)}\right\}=GNN(\left\{p_i^{\left(l\right)}\right\},A)$$

其中 $\left\{p_i^{\left(l\right)}\right\}$ 是多线段节点的集合。 $GNN(.)$ 对应的单层的图神经网络。A对应节点的邻接矩阵，它能够提供节点之间的距离之类的信息。我们假设A是一个全连接的图，图网络可以表达成self-attention:

$$GNN(P)=softmax\left(P_Q{P}_K^T\right)P_V$$

其中$P$是节点特征矩阵，$P_Q$，$P_V$，$P_K$ 是线性投影。

作者将移动的智能体的未来轨从节点中进行解码：

$$v_i^{future}={\phi }_{traj}\left(P_i^{L_t}\right)$$

其中$L_t$是GNN层总数的数目，而${\psi }_{traj}(.)$是轨迹解码器。为了简单起见，我们使用MLP来解码。

在实现中使用单个GNN层，在推理期间，仅需要计算与agent相对应的节点特征。如果有必要，也可以堆叠多层 $GNN(.)$来建模进行高阶交互。

为了让全局交互图更好地捕捉不同轨迹和map polyline之间的交互，这里引入了一个辅助图完成任务。在训练期间，我们随机掩盖polyline节点的子集的特征，然后尝试将其屏蔽功能恢复为：

$${\hat{\mathbf{p}}}_i={\phi }_{\text{node }}\left({\mathbf{P}}_i^{\left(L_t\right)}\right)$$

其中${\phi }_{node}\left(.\right)$ 是实现MLP解码的节点特征，这些特征不用于推断的时候。$P_i$ 是来自全连阶层的节点。为了能够区分独立的polyline节点是对应的特征被隐藏的，计算起始坐标的最小值得到$P_i^{id}$,这些输入的节点特征变成

$$P_i^0=\left[P_i；P_i^{id}\right]$$

4.整体框架

一旦构建了分层图网络，针对多任务培训目标进行优化

$$\mathcal{L}={\mathcal{L}}_{\text{traj }}+\alpha {\mathcal{L}}_{\text{node }}$$

其中，$L_{traj}$是未来真实轨迹的负高斯对数似然，$L_{node}$是在预测的节点特征和真值之间Huber损失，$\alpha$=1.0是平衡两者的损失标量。作者在将polyline节点特征馈送到全局图网络之前对其进行L2归一化。

其他交通参与者采用的是相对偏移，起点是上一帧对目标agent的观测，并且基于上一帧目标agent观测位置的heading建立相对坐标系。

我们对多段线子图使用三个图层，对全局交互图使用一个图层。所有MLP中隐藏单位的数量固定为64。MLP之后是归一化和ReLU非线性。我们以车辆最后观测到的位置为中心，将矢量坐标归一化。VectorNet在8个GPU上同步训练使用Adam optimizer。学习速率每5分钟衰减一次按因子0.3计算，我们训练模型的总时间为25个回合，初始学习率为0.001。

实验验证

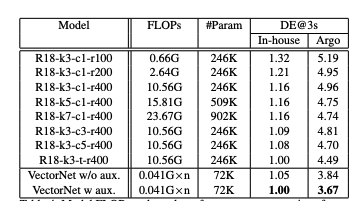
VectorNet相比ResNet-18系列相比，参数量仅为29%，计算量小仅为20%，效果提升18%，真正地实现了更小，更快，更强。