黏菌算法优化长短期记忆神经网络原理及MATLAB代码复现

最新推荐文章于 2025-05-21 12:04:25 发布

成哥MATLAB智能算法

最新推荐文章于 2025-05-21 12:04:25 发布

阅读量1k

点赞数 14

分类专栏：长短期记忆神经网络智能算法文章标签：算法神经网络 matlab 机器学习深度学习

本文链接：https://blog.csdn.net/2403_88401503/article/details/148109090

版权

智能算法同时被 2 个专栏收录

132 篇文章

订阅专栏

长短期记忆神经网络

49 篇文章

订阅专栏

0 引言

黏菌算法（Slime Mould Algorithm，SMA）是学者Li等人于2020年提出的一种启发式智能算法，该算法模拟黏菌感知食物时表现出振荡模式，而，同时食物源的数量和质量还会影响静脉的状态，加大黏菌探索未知领域。

1 数学模型

SMA算法的的数学模型是黏菌觅食表现出接近食物、包围食物及抢夺食物进行构建，具体数学模型如下：

1）接近食物：黏菌能够根据空气中的气味接近食物，为了用数学公式来表达它的接近行为，提出了以下公式来模拟接近模式。

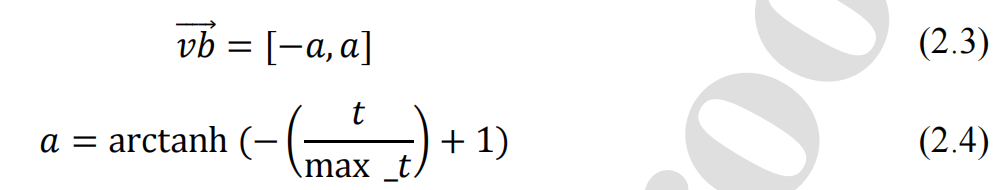
式中𝑣𝑏是一个参数，范围为[−𝑎，𝑎]，𝑣𝑐从1线性递减到0。𝑡表示当前迭代次数，𝑋𝑏表示当前找到的气味浓度最高的位置，𝑋表示黏菌的位置，𝑋𝐴和𝑋𝐵代表从黏菌中随机选出的两个人，𝑊代表黏菌的重量。𝑝的概率因子。𝑖∈1,2，...，𝑛，𝑆（𝑖）表示𝑋的适应度，𝐷𝐹表示所有迭代中获得的最佳适应度。𝑐𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛表示𝑆（𝑖）排名前半部分人口，𝑟表示[0,1]区间内的随机值，𝑏𝐹表示当前迭代过程中获得的最佳适应度，𝑤𝐹表示当前迭代过程中获得的最差适应度值，𝑆𝑚𝑒𝑙𝑙𝐼𝑛𝑑𝑒𝑥表示按最小值问题排序的适应度值序列。

2）包围猎物：包围猎物主要模拟了黏菌在搜索时静脉组织结构的收缩模式。接触食物浓度越高，生物振荡器产生的波越强，细胞质流动速度越快，静脉也越粗。黏菌静脉宽度与食物浓度之间的正负反馈关系。成分𝑟模拟了黏菌和食物浓度探索过程中的不确定性。𝑙𝑜𝑔用于减轻数值变化率，使收缩频率值不会变化太大。𝑐𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛模拟了黏菌根据食物质量调整其搜索模式的过程。当食物浓度较高时，该区域附近的权重较大；当食物浓度较低时，该区域的权重会减少，从而转向探索其他区域。基于上述原理，更新黏菌位置的数学公式如下：

式中𝐿𝐵和𝑈𝐵，𝑟表示随机值，表示在[0,1]下的下限和上限，𝑧的值将在搜索范围、𝑟𝑎𝑛𝑑实验的参数。

3）抢夺食物：黏菌主要依赖生物振荡器产生的传播波来改变细胞质在脉管中的流动，使其更倾向于处于食物浓度较高的位置。为了模拟黏菌脉管宽度的变化，我们使用了𝑊、𝑣𝑏和𝑣𝑐来实现这些变化。不同的食物浓度使得𝑊能够数学模拟黏菌的振荡频率，当黏菌接近高质量食物时，它们可以更快地接近食物；而当食物浓度较低时，黏菌则会更缓慢地接近食物，从而提高了黏菌选择最佳食物来源的效率。𝑣𝑏的值在[−𝑎，𝑎]之间随机振荡，并随着迭代次数的增加逐渐接近零。𝑣𝑐的值在[-1,1]之间振荡，最终趋向于零。𝑣𝑏和𝑣𝑐的变化趋势模仿了黏菌的选择行为。

2 优化方式

前篇对长短期记忆神经网络（长短期记忆神经网络原理及Matlab代码复现-CSDN博客）原理讲解，从长短期记忆神经网络matlab代码运算过程中，可以看到LSTM受多个超参数影响（隐藏层节点、学习率、分批量、正则化等等）。因此结合上述SMA原理介绍，可以将长短期记忆神经网络的超参数作为黏菌个体位置，每一个种群位置对应长短期记忆神经网络的预测值，将这个预测值作为适应度进行黏菌觅食行为，进行下一迭代黏菌觅食。

3 MATLAB代码

3.1 伪代码

3.2 主函数代码

while  it <= Max_iter
            
    for i=1:N
        % 边界检查
        Flag4ub=X(i,:)>ub;
        Flag4lb=X(i,:)<lb;
        X(i,:)=(X(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        AllFitness(i) = SYD(X(i,:),net);
        net.trainParam.showWindow = 0;
    end
    
    [SmellOrder,SmellIndex] = sort(AllFitness);  %Eq.(2.6)
    worstFitness = SmellOrder(N);
    bestFitness = SmellOrder(1);

    S=bestFitness-worstFitness+eps;  %  eps为了避免分母为0

    %计算每种粘菌的健身重量
    %对黏菌的静脉直径与所调查的食物含量之间的正负反馈回路进行模拟
    for i=1:N
        for j=1:dim
            if i<=(N/2)  %Eq.(2.5)
                weight(SmellIndex(i),j) = 1+rand()*log10((bestFitness-SmellOrder(i))/(S)+1);
            else
                weight(SmellIndex(i),j) = 1-rand()*log10((bestFitness-SmellOrder(i))/(S)+1);
            end
        end
    end
    
    %更新最优适应度和其对应位置
    if bestFitness < Destination_fitness
        bestPositions=X(SmellIndex(1),:);
        Destination_fitness = bestFitness;
    end
    
    a = atanh(-(it/Max_iter)+1);   %Eq.(2.4)
    b = 1-it/Max_iter;

    % 根据上述理论更新黏液的位置
    for i=1:N
        if rand<z     
            X(i,:) = (ub-lb)*rand+lb;%Eq.(2.7)a
        else
            p =tanh(abs(AllFitness(i)-Destination_fitness));  %Eq.(2.2)
            vb = unifrnd(-a,a,1,dim);  %Eq.(2.3)
            vc = unifrnd(-b,b,1,dim);
            for j=1:dim
                r = rand();
                A = randi([1,N]);  % 从种群位置中随机抽取的两个
                B = randi([1,N]);
                % 接近食物的公式
                if r<p 
                    X(i,j) = bestPositions(j)+ vb(j)*(weight(i,j)*X(A,j)-X(B,j));%Eq.(2.7)b
                else
                    X(i,j) = vc(j)*X(i,j);%Eq.(2.7)c
                end
            end
        end
    end
    Convergence_curve(it)=Destination_fitness;
    it=it+1;
end

end