《电路原理》学习笔记1-3：基尔霍夫定律

1.有关的电路术语

（1）支路：在电路中，每个二端元件构成一条支路。我的个人理解是，一条支路最重要的就是它的两端和连接的元件，它的两端决定了这条支路和其他支路的连接关系，元件决定了这条支路上满足怎样的电学性质。

（2）节点：在电路中，每条支路的端点称为节点。当有多条支路的连在同一个点上的时候，这个连接点就属于这些支路“共有”的了，也就是说这里实际上就只有一个节点了。而只关联两条支路的节点就被称为简单节点。

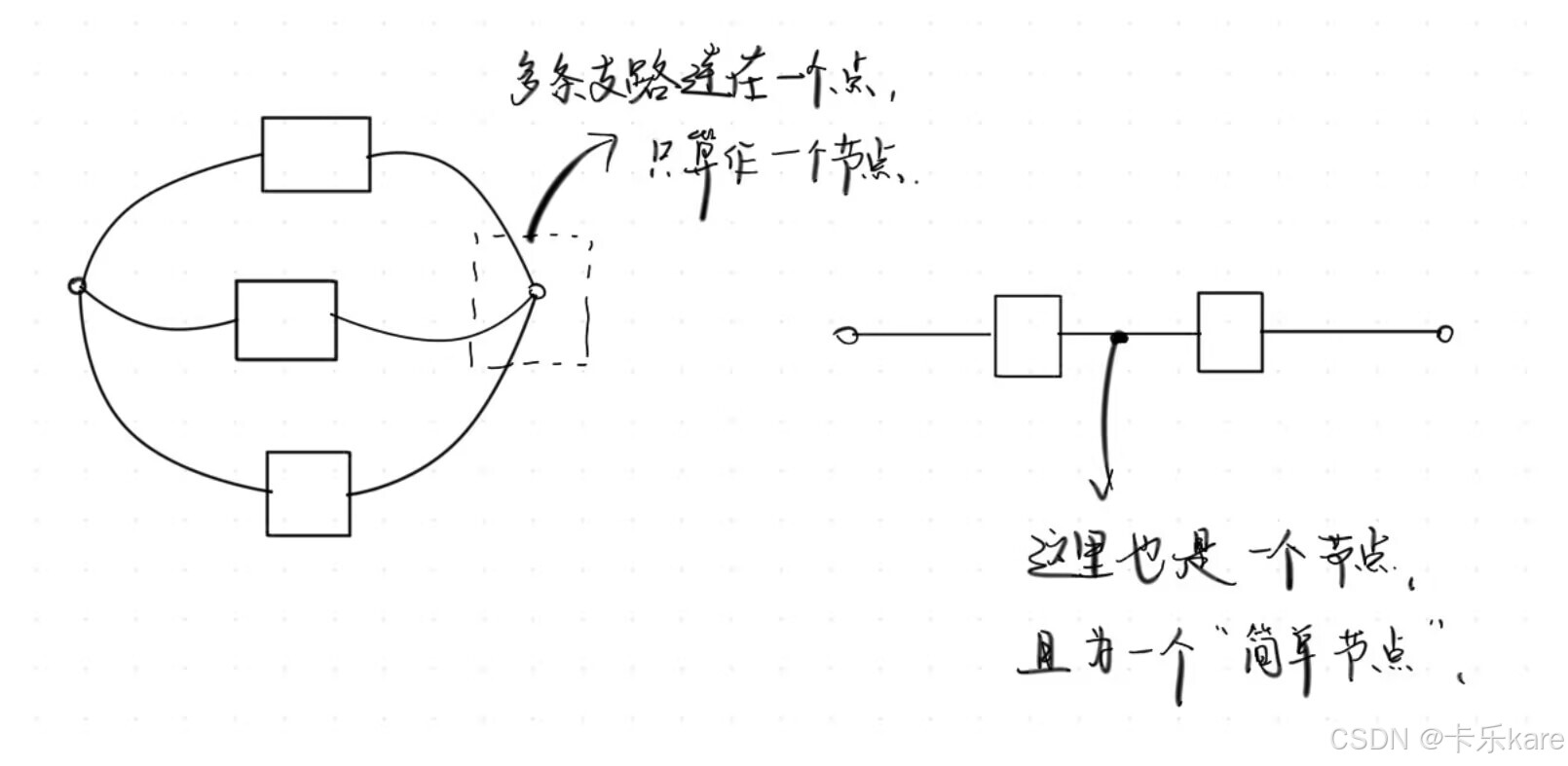
（3）回路：书上的解释是：“在集中参数电路中，由若干条支路构成的，其中每一个节点与两条支路（且只与两条支路）相联接的闭合路径称为回路”，我觉得通俗来讲，只要能形成闭合回环并且没有短路，应该就能形成一个回路。（这个说法有些过于粗糙，但是很方便理解了，如果有误请好心人指正）

2.基尔霍夫电流定律

基尔霍夫电流定律所描述的就是对于集中参数电路中的任何一个节点，在任意时刻，流入此节点的电流之和等于流出此节点的电流之和，就相当于，有很多根水管连在一个点上，这个点的水都是时时刻刻在流动的，不会有水留在这里不动，于是流入的水就等于流出的水。

但是一般在列写方程的时候，我们都会把电流项全部放在左边，右边只剩下0，如果电流是流入节点，就加上这个电流，如果电流是流出节点，就减去这个电流。特别要注意的是，这里我们不会考虑电流的正负，只根据电路图中电流的方向来决定方程中电流前的系数是正还是负，如果最后算出来电流的代数值为负，就说明这里的电流和电路图中标出来的是相反的。

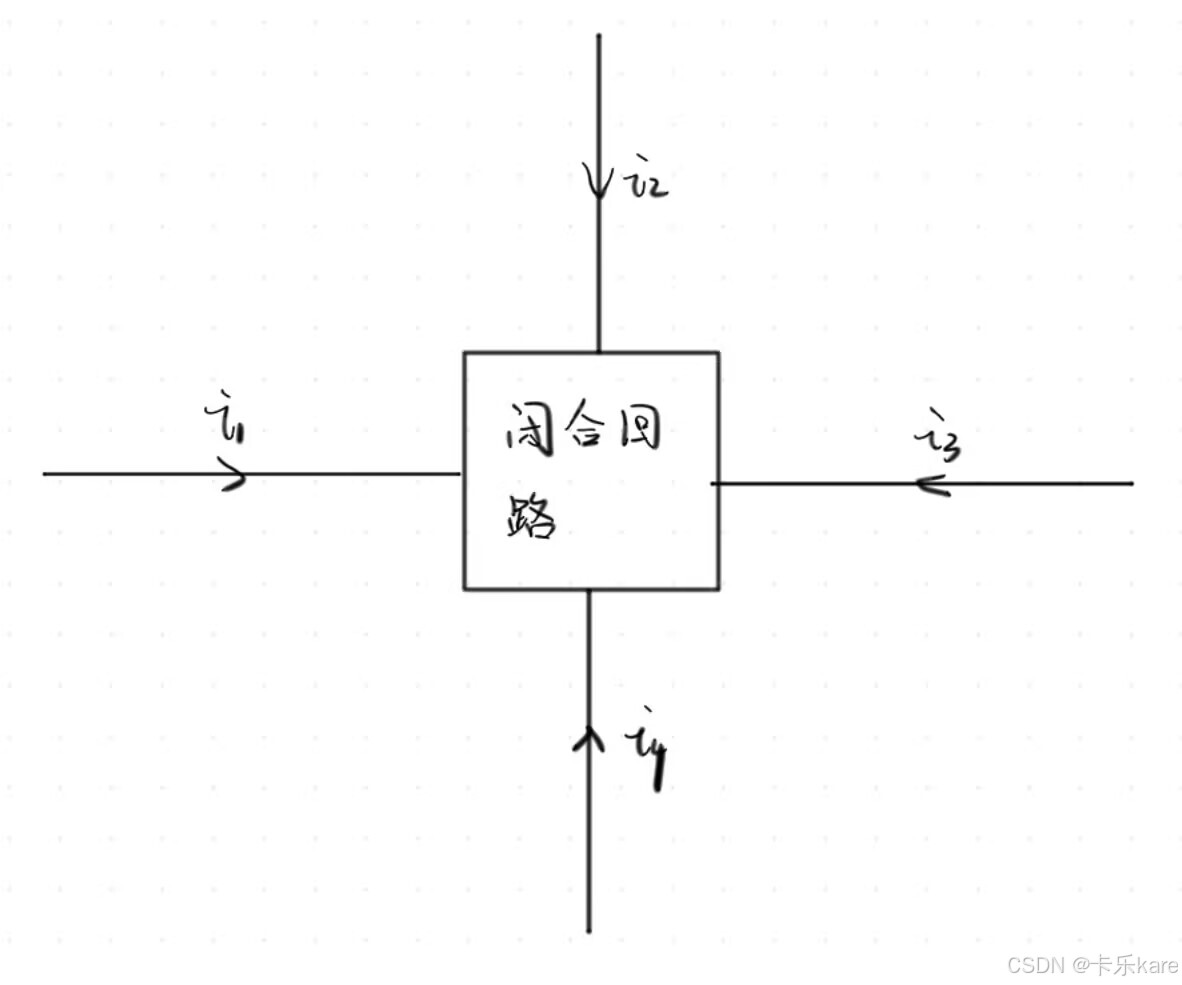
在上面这样的一个部分中，流入闭合回路的电流代数和也是0（可以由关联的基尔霍夫电流方程相加而得），这个闭合回路也可以看作是一个节点，被称为广义节点。通常，这个闭合回路都是我们人为划定出来的，一般都是在不考虑划定范围内回路的电流时，为了简化计算才使用广义节点的方法。

3.基尔霍夫电压定律

基尔霍夫电压定律是讲，在集中参数电路的任何一个回路当中，在任意时刻，沿着某个确定方向（顺时针或逆时针）计算，各支路的电压代数和恒为零。我的通俗理解是，分析整个电路的电位，每个节点都在一个同样高的台阶上，经过一个支路后，电位或是上升或是下降，来到另一个不同高度的台阶上。当我们沿着一个回路走的时候，走完一圈总会回到原来的位置，而不会凭空上升或者下降。

在列写方程的时候，我的个人习惯是，一个支路电压降低，就加上降低的电压（数值），如果电压升高，就减去升高的电压，这样方程的右边就可以为0。

其实更多时候，我采用的方式是假设某个节点的电位为0，然后一步一步推出其他节点的电位，最后回到假设电位为0的这个节点，这时候我们只需要写回到这个节点的时候电位的表达式等于零就可以了，计算过程如图：（计算us）

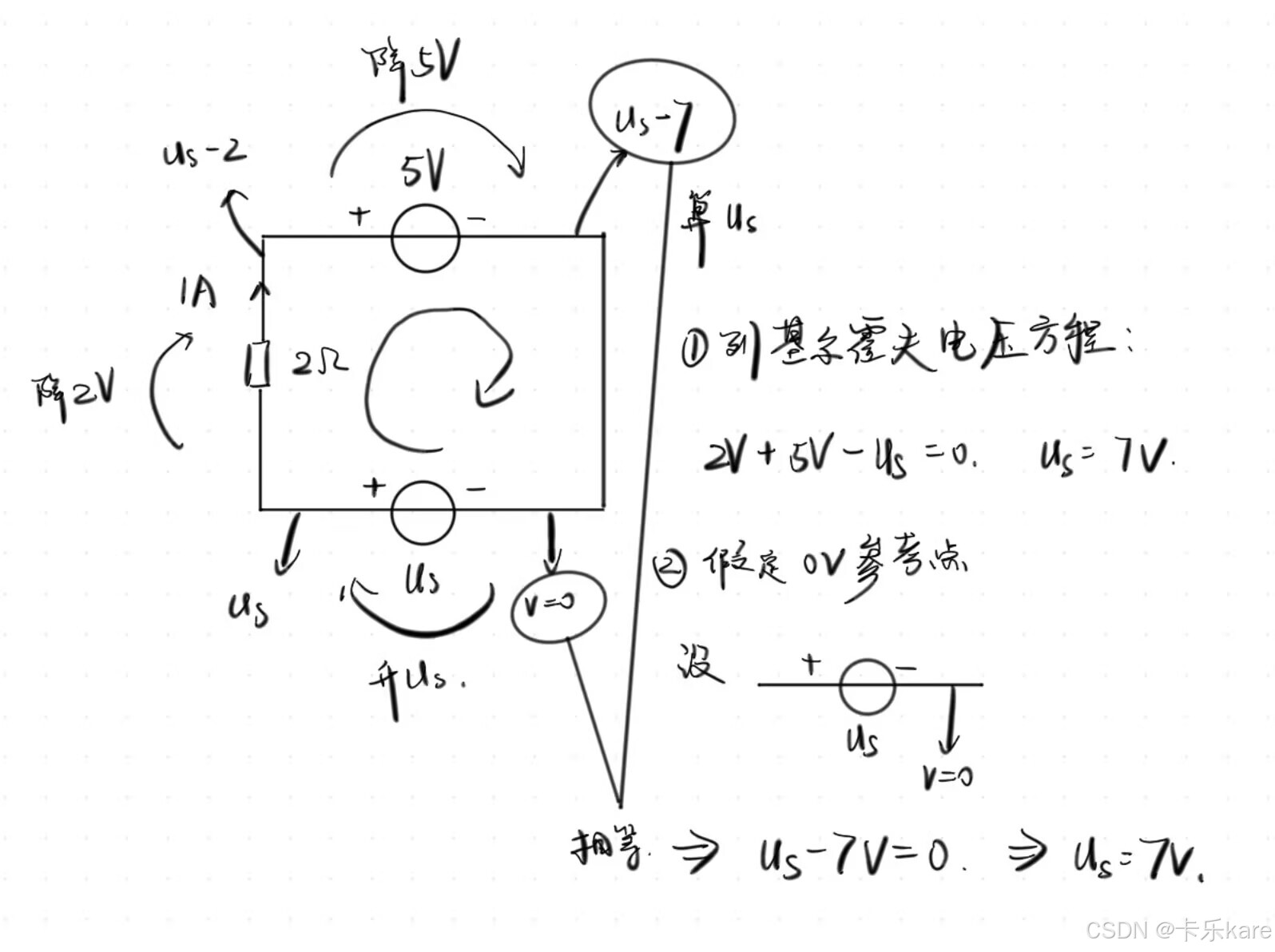
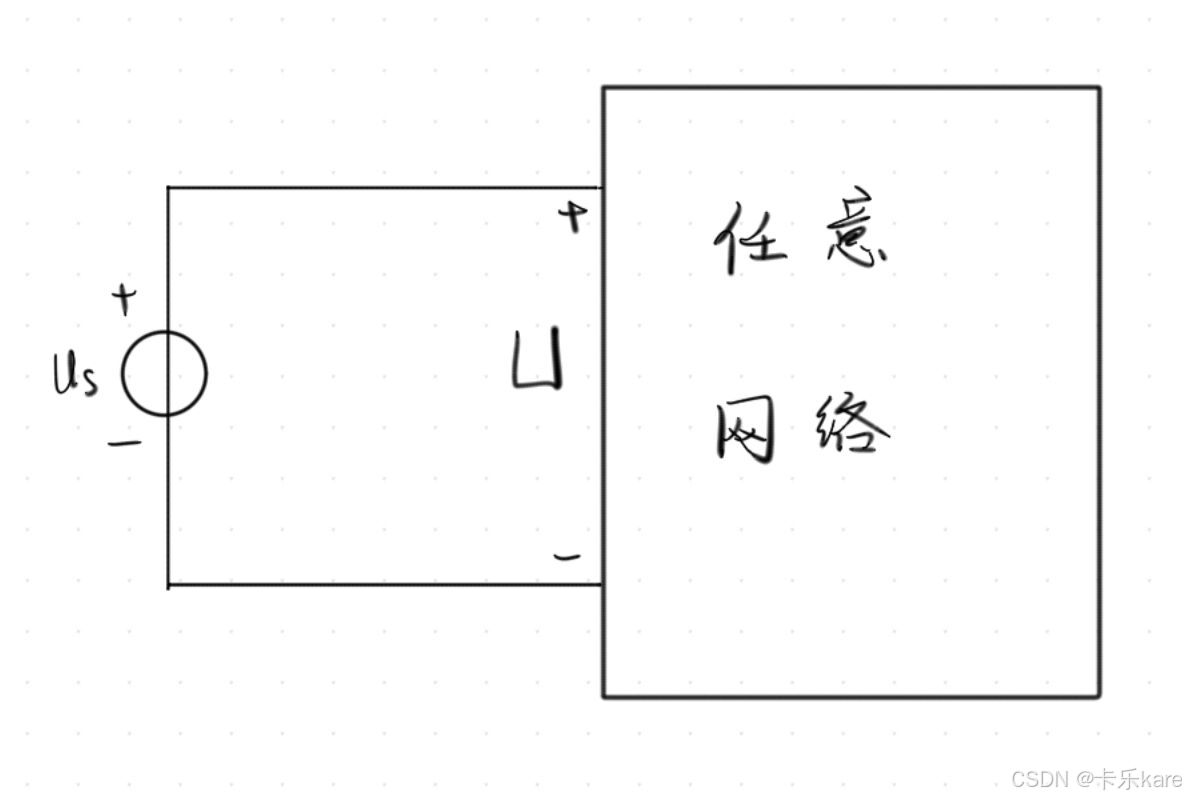
如上图，我们也可以不考虑右侧网络内部的电压变化，把整个网络作为一个节点，就构成了一个“假想的”回路，这时基尔霍夫电压定律依然成立，也就是us - u = 0。使用假想回路的方法，我们也可以快速列出含有目标量的基尔霍夫电压方程。