圆锥曲线焦点三角形内心的坐标公式

在高中数学中，有时候会出现关于圆锥曲线焦点三角形内心的有关问题，通常而言这是非常棘手的，因为内心的几何性质不像外心那样能够用坐标直接表示出来，在做题的过程中就需要作角平分线，内切圆等等，我自己当初做这类题的时候是感觉非常困难的。

所以我就在想，能否直接以公式的方式把圆锥曲线焦点三角形内心的坐标写出来。在高三的时候，我推出了这个公式，并且用起来是相当方便且暴力的。其实我的数学能力很有限，分析问题的时候常常脑筋转不过弯来，于是我在高中的时候就热衷于开发各种暴力求解方法，比如建斜坐标系，我在推导这个公式的时候也用到了斜坐标系。

现在我已经上了大学，按理说应该不对高中数学再有什么交集了，而且我考试的时候也从来没用到过这个公式，但是这个公式我个人非常喜欢，于是我想着把它和它的推导过程发出来。

我的推导思路主要是两步，第一步是推导出一般三角形的内心的向量表示式，第二步是在这个表示式的基础上推导出圆锥曲线焦点三角形内心的坐标表示式。

1.斜坐标系的引入

我们现在先进行第一步。对于一般的三角形，我们很难建立一个合适的直角坐标系来表示它各点的坐标，即使能建系，坐标的表示也不是很简洁。于是我想到可以建立一个斜着的坐标系，这个坐标系是为我们研究的三角形“量身定制”的。

所谓的建立斜坐标系，其实就是换基底。直角坐标系中的基底是两个互相垂直的单位向量，那么在斜坐标系中的基底就是两个成一般角度的单位向量。这样一来，我们就可以对比一下这两种坐标系表达同一个三角形的区别。

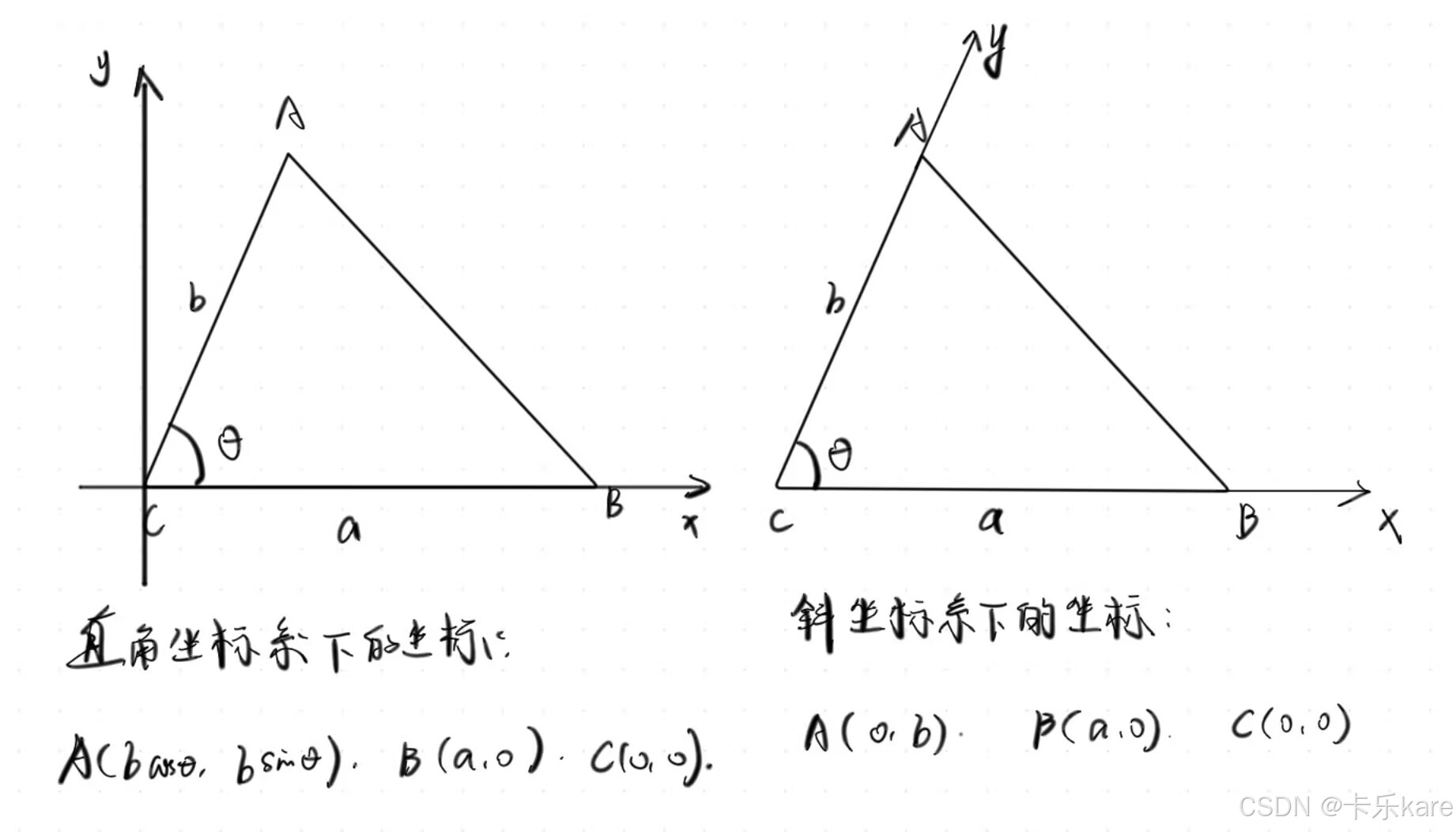
在直角坐标系中，已知两点的坐标，求通过这两点直线的方程，我们可以用两点式直线方程写出，那么在斜坐标系下，这个方法依然适用吗？做一个证明：

由此可见，直角坐标系中用两点的坐标表示一条直线的方程的方式在斜坐标系中依然适用。

2.一般三角形内心的向量表示式

在掌握了斜坐标系这一工具后，我们可以着手推导一般三角形内心的向量表示式了。首先明确内心的定义：在三角形中三个角的角平分线交于一点，这一点就是该三角形的内心。

那么一个很自然的想法就是，在斜坐标系中写出两条角平分线的方程，然后联立求出内心的坐标，进而写出向量表示式。原点处的角平分线的方程很简单，就是y=x，这里给一个简单的证明：

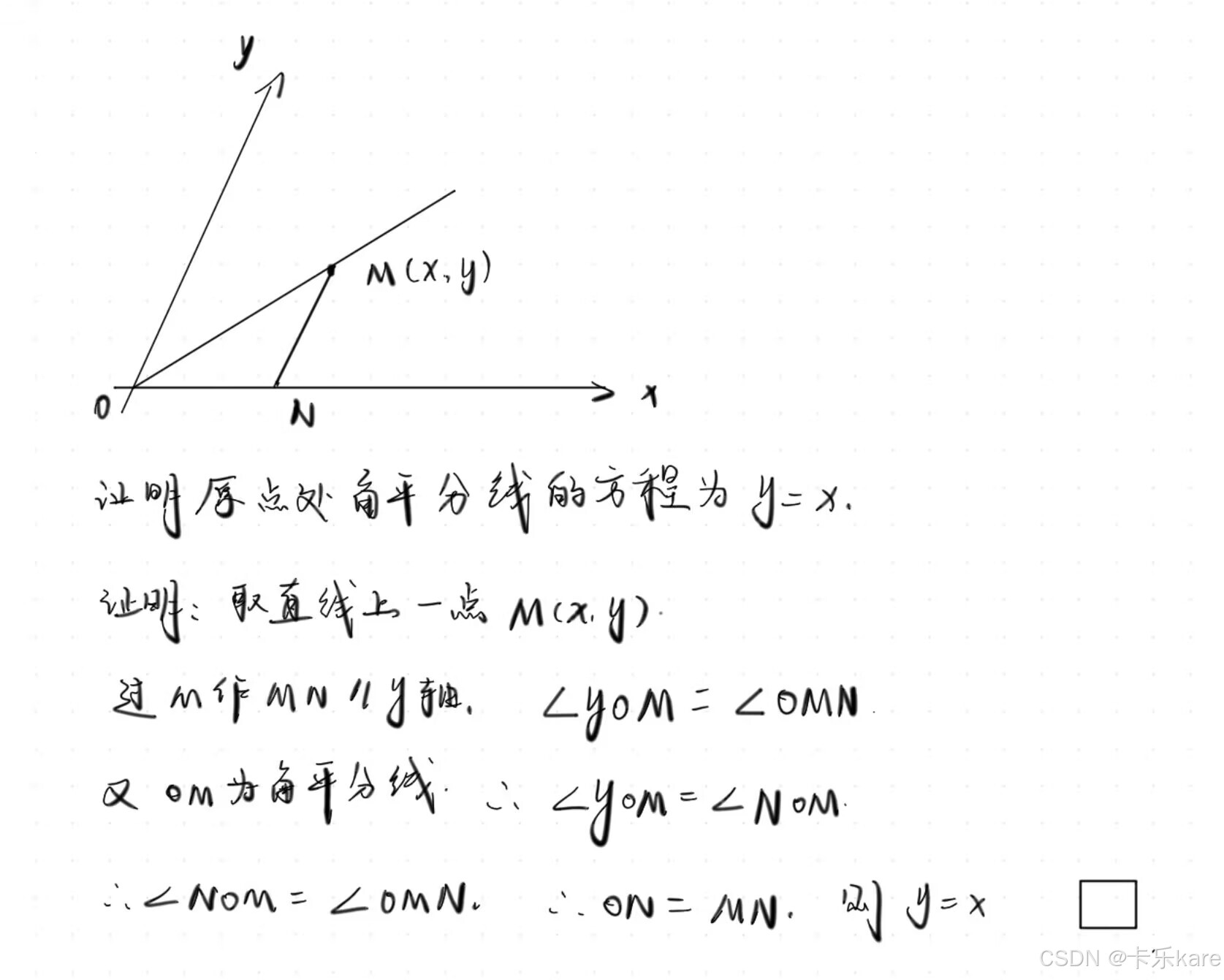
这样一来，我们就解决了一条角平分线的问题，现在我们的主要问题就是写出另一条角平分线的方程了。这也是整个推导过程中最困难的一部分。这里我们将用到一些线性代数的知识。

首先，在直角坐标系中我们有一个结论，已知三点的坐标(x1,y1),(x2,y2),(x3,y3)，如果这三点能构成三角形的话，这个三角形的面积就是，如果算出来是负数的话取绝对值就行了。但是现在我们是在斜坐标系中分析三角形，就不能继续直接用这个公式了。

实际上，我们所用的斜坐标系其实就是对直角坐标系进行了一个线性变换，用矩阵表示的话，直角坐标系就是，其中和分别代表两个基底向量，那么斜坐标系用矩阵表示就应该是，其中θ代表的是斜坐标系x轴正方向和y轴正方向所成的角度。那么在进行这样一次线性变换后，原直角坐标系内的所有几何图形的面积大小都会变为原来的倍，也就是sinθ倍。由此可知：在倾斜角为θ的斜坐标系中，已知三点的坐标(x1,y1),(x2,y2),(x3,y3)，如果这三个点能够构成三角形，那么这个三角形的面积就为：。这个结论会在稍后的推导中用到。

现在我们要回到我们要解决的问题了：求出另一条角平分线的方程。求解过程如下：

由此可以求得I的坐标为(,).那么 =  + .

同理，有 =  + ， =  + .

以上就是一般三角形内心的向量表示式。

3.圆锥曲线焦点三角形内心的坐标公式

现在，我们可以借助上面推导的三角形内心的向量表示式来写出圆锥曲线焦点三角形内心的坐标了：

对于椭圆：

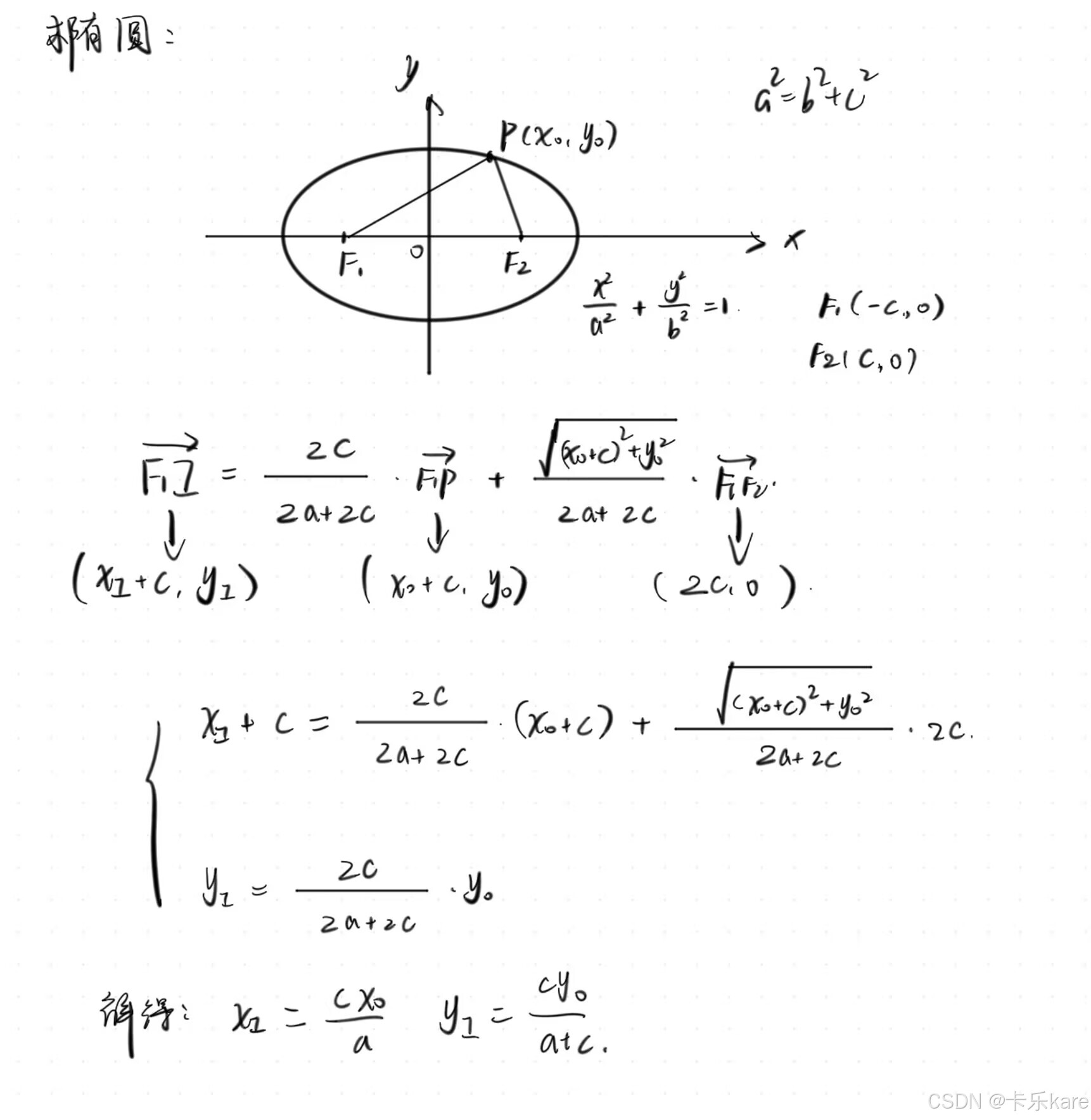
同理，对于双曲线：

双曲线比较特殊，它的焦点三角形的内心横坐标是一个定值，它一定在双曲线顶点的上方或下方，这也是我们高中当时需要记住的一个结论。

解的过程比较繁琐，感兴趣的话可以自行计算，我就直接把结果写出来了。

最后我们得到了圆锥曲线焦点三角形内心的坐标公式：

对圆锥曲线上任意一点P(,)，其与两个焦点构成的三角形的内心坐标为：

椭圆：(,)；双曲线：当≥a时，坐标为(a,)，当≤-a时，坐标为(-a,).