基于高斯过程的声场估计区域限制传感器布置（Matlab代码实现）

最新推荐文章于 2025-10-08 20:56:16 发布
最新推荐文章于 2025-10-08 20:56:16 发布
阅读量716 收藏 7
点赞数 19
CC 4.0 BY-SA版权
文章标签： matlab 人工智能 机器学习 支持向量机
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2501_93142541/article/details/152706462

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

基于高斯过程的声场估计区域限制传感器布置研究

 本文提出了基于高斯过程的场估计传感器布置方法。一般来说，传感器布置方法通过从预定义的候选位置中选择适当的位置来确定布置位置。已经提出了许多用于选择的标准，这些标准评估了候选位置处场的布置质量。这意味着这些传感器布置方法旨在找到能够准确估计候选位置处场的位置。然而，在实际情况下，候选传感器布置区域可能与场估计的目标区域不同。为了使传感器布置方法适用于这种情况，本文提出了两种基于均方误差和条件熵的传感器布置方法，可应用于传感器布置区域受任意限制的情况。在制定传感器布置问题后，导出了两种近似算法：贪婪算法和基于凸松弛的算法。还说明了所提方法在声场估计中的应用，并通过数值实验验证了其有效性。

估算或插值物理场，比如温度 [1]，[2]，声场 [3]–​[5]，和污染 [6]，从传感器测量的数值中是一个具有许多应用的重要问题。例如，声场估计是一个在许多情况下使用的问题，例如使用扬声器或耳机重现声场，可视化和主动噪声控制。为了估算场，多个传感器被分布在目标区域中，并且整个场是根据它们的测量来估计的。

由于物理或经济约束，可以放置的传感器数量通常受到限制。在这种情况下，传感器的位置对估算精度有很大影响。因此，场估计中的一个主要问题是如何确定分布传感器的布置。为了解决这个问题，已经进行了大量关于传感器布置方法的研究。例如，在声学问题的背景下，传感器布置方法已经应用于声场估计 [7]，麦克风阵列设计 [8]，和声场控制 [9]，[10]等问题。在大多数方法中，首先将感兴趣的区域离散化，然后从这些离散化的位置确定适当的传感器位置，直到达到限定数量。文献中提出了许多选择位置的标准，这些标准基于观测模型，例如高斯过程 (GPs) [11]–​[13] 和有限维线性逆问题 [14]–​[16]。尽管有各种各样的标准，但大多数评估离散化位置处的场，这些位置也用作候选传感器位置。详细文章见第4部分。

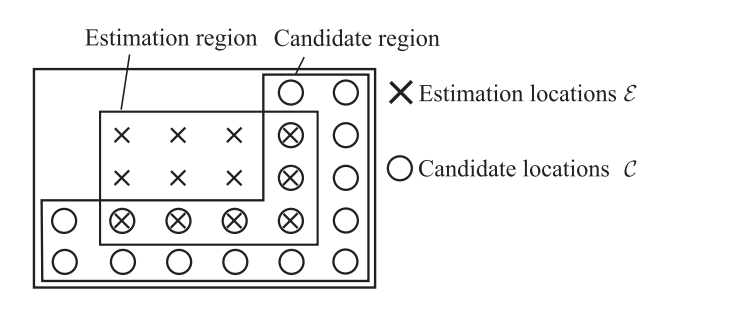
一、研究背景与意义

无线传感器网络（WSN）在声场估计领域展现出巨大潜力，通过部署低成本传感器节点，可实时获取空间声学数据，为智能建筑声学优化、工业噪声监测等提供关键信息。然而，实际应用中传感器布置面临多重限制：

  1. 物理空间限制：如古建筑监测中，文物保护要求限制传感器安装位置；工业场景中高温、高压、强电磁干扰等环境限制部署区域。
  2. 成本约束：大规模WSN部署总成本高，需在有限预算下实现高效布置。
  3. 能源限制：电池供电传感器在野外、深海等场景中难以更换电池，需降低能耗以延长寿命。

传统随机部署方式难以保证估计精度，而穷举搜索所有布置方案计算成本过高。因此，在区域限制条件下高效选择传感器位置成为WSN声场估计的关键问题。高斯过程（Gaussian Process, GP）作为一种非参数贝叶斯方法，为解决该问题提供了新思路。

二、高斯过程基本原理

高斯过程是一族随机变量的集合，其中任意有限个随机变量的联合分布服从多维正态分布。在声场估计中：

  • 输入：传感器位置（空间坐标）。
  • 输出：声压值。
  • 建模过程：通过已知位置的声压数据，高斯过程学习输入（位置）与输出（声压）的关系，构建概率模型。对任意新位置，高斯过程不仅预测声压值，还提供预测的不确定性估计（如置信区间）。

核函数选择：

  • 径向基核函数（RBF）：衡量输入点距离，捕捉数据局部特征，应用广泛。
  • 多项式核函数：适用于非线性关系建模。
三、高斯过程在声场估计中的优势
  1. 噪声处理能力：
    • 传统插值方法（如最近邻、线性插值）对复杂声场分布和噪声干扰的估计精度低。
    • 高斯过程将噪声视为模型一部分，通过调整核函数参数和噪声方差，适应不同噪声水平，提高估计精度。
  2. 预测置信区间：
    • 提供预测结果的可靠性信息。窄置信区间表示高信心预测，宽置信区间提示不确定性，指导决策（如判断噪声是否超标或调整音响系统）。
四、区域限制条件下的挑战
  1. 计算复杂度高：
    • 高斯过程计算复杂度与传感器数量立方成正比，大规模WSN中计算资源消耗大，实时性难以满足。
  2. 传感器位置选择复杂：
    • 物理空间、成本、能源限制导致传感器需在有限区域内布置。
    • 随机部署可能导致分布不均，关键区域未覆盖；穷举搜索计算成本过高。
五、传感器布置优化策略

优化目标：在区域限制条件下最大化声场估计精度，常用衡量指标为预测方差和预测均方误差（MSE）。

优化方法：

  1. 贪婪算法：
    • 迭代选择能最大程度降低预测方差或MSE的传感器位置，直至达到预设数量或满足约束。
    • 优点：简单高效。
    • 缺点：可能陷入局部最优解。
  2. 模拟退火算法：
    • 概率性全局优化算法，通过温度参数控制搜索过程，避免局部最优。
    • 优点：全局搜索能力强。
    • 缺点：收敛速度较慢。
  3. 遗传算法：
    • 基于自然选择机制，通过种群进化迭代优化传感器布置方案。
    • 优点：全局搜索能力强，可处理复杂约束。
    • 缺点：计算复杂度较高。
  4. 基于信息论的优化方法：
    • 如最大熵方法，通过最大化信息增益或最小化不确定性选择传感器位置。

改进方向：

  • 结合改进贪婪算法、混合算法等提高优化效率和精度。
  • 考虑实际应用约束（如通信距离限制、障碍物存在），将约束条件融入优化模型。
六、实验与评估
  1. 仿真实验：
    • 通过数值实验验证优化方法的有效性，比较不同算法的预测精度、计算时间和部署便利性。
  2. 实际部署实验：
    • 在真实场景中部署传感器，评估优化方法的实际性能。

评估指标：

  • 预测精度：预测方差、MSE。
  • 计算时间：算法运行时间。
  • 部署便利性：传感器布置的难易程度。
七、应用案例
  1. 智能建筑声学优化：
    • 通过优化传感器布置，实时监测室内声场分布，调整音响系统参数以优化声学效果。
  2. 工业噪声监测：
    • 在复杂工业场景中部署传感器，监测噪声水平，为噪声控制提供依据。
八、未来研究方向
  1. 高斯过程模型参数优化：
    • 研究更高效的核函数参数调优方法，提高模型适应性。
  2. 更高效的优化算法：
    • 开发适用于大规模WSN的全局优化算法，降低计算复杂度。
  3. 多模态传感器融合：
    • 结合声学、温度、振动等多模态传感器数据，提高声场估计的全面性和准确性。

📚2 运行结果

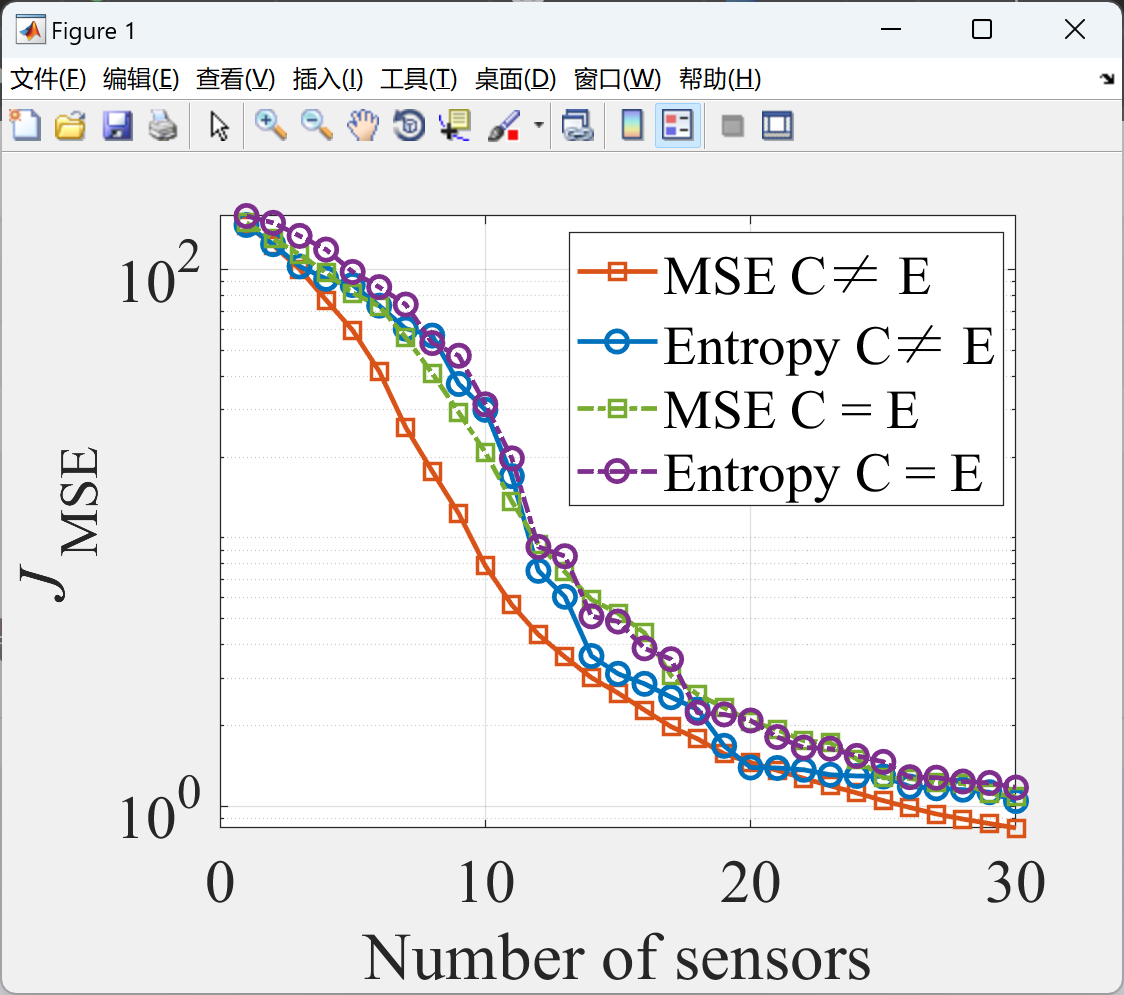
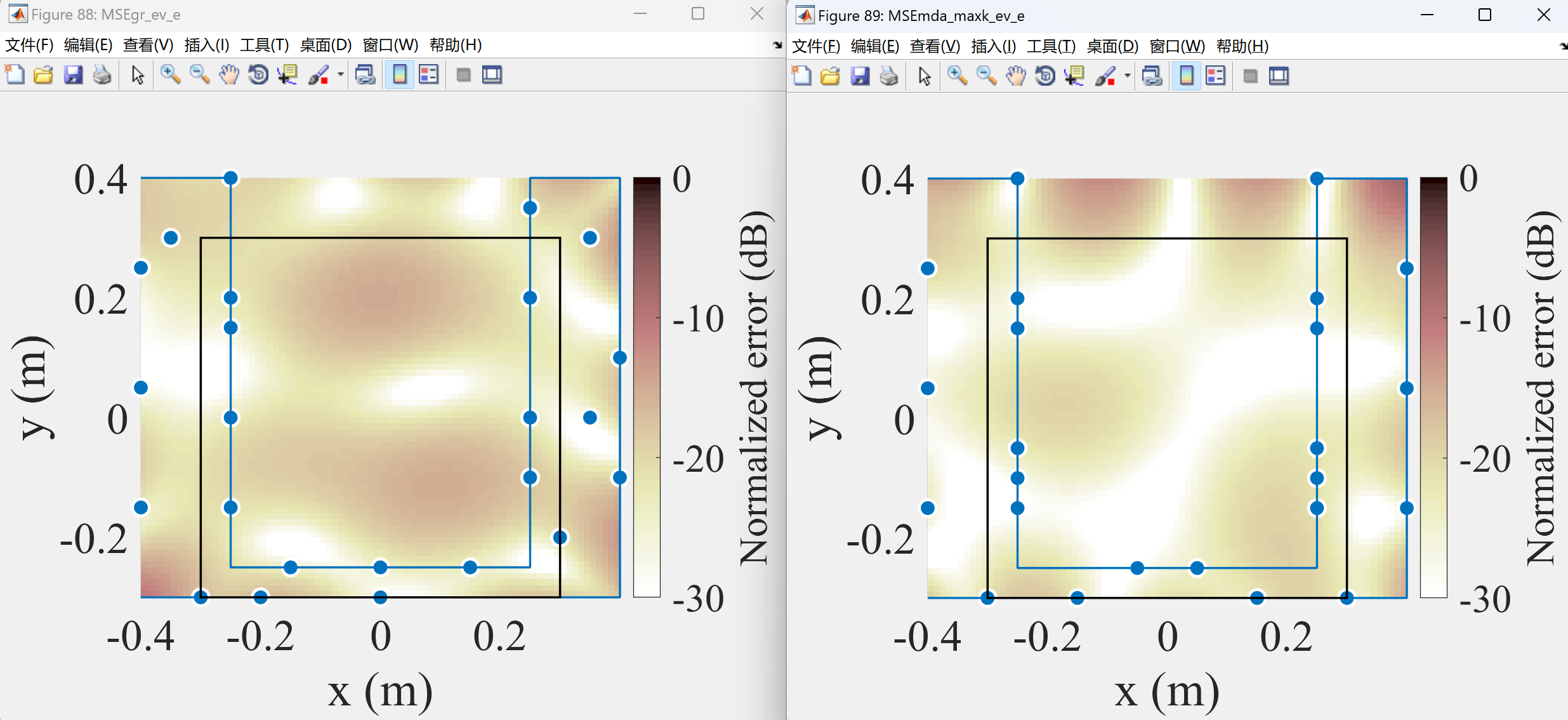
部分代码：

%mic vs cost
for kk = 1:prm.freq_len
       
    figure();
    semilogy(MSEevcost_Aoptgr_ev(kk,:),'s-','Color', red, 'MarkerSize', Msize, 'DisplayName', 'MSE C\neq E');
    hold on;
    semilogy(MSEevcost_Doptgr_ev(kk,:),'o-','Color', blue, 'MarkerSize', Msize, 'DisplayName', 'Entropy C\neq E');
    semilogy(MSEevcost_Aoptgr_cd(kk,:),'s-.','Color', green, 'MarkerSize', Msize, 'DisplayName', 'MSE C = E');
    semilogy(MSEevcost_Doptgr_cd(kk,:),'o-.','Color', purple, 'MarkerSize', Msize, 'DisplayName', 'Entropy C = E');
    hold off;
    grid on;
    xlabel('Number of sensors'); ylabel('\sl{J}_{\rm MSE}');
    legend('Location','best');
    figname = sprintf('%s/MSEcost_f%d.png',dir_name, prm.freq(kk));        
    saveas(gcf, figname);
        
    figure();
    hold on;
    plot(ENTevcost_Aoptgr_ev(kk,:),'s-','Color', red, 'MarkerSize', Msize, 'DisplayName', 'MSE C\neq E');
    plot(ENTevcost_Doptgr_ev(kk,:),'o-','Color', blue, 'MarkerSize', Msize, 'DisplayName', 'Entropy C\neq E');
    plot(ENTevcost_Aoptgr_cd(kk,:),'s-.','Color', green, 'MarkerSize', Msize, 'DisplayName', 'MSE C = E');
    plot(ENTevcost_Doptgr_cd(kk,:),'o-.','Color', purple, 'MarkerSize', Msize, 'DisplayName', 'Entropy C = E');
    hold off;
    grid on;
    xlabel('Number of sensors'); ylabel('\sl{J}_{\rm ENT}');
    legend('Location','best');
    figname = sprintf('%s/ENTcost_f%d.png',dir_name, prm.freq(kk));        
    saveas(gcf, figname);            
    
end 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据、文章下载

基于高斯过程的声场估计区域限制传感器布置附Matlab代码
j_jinger的博客
10-07 547
输入输出映射：将传感器空间坐标（二维 / 三维）作为输入，声压值作为输出，通过已知传感器数据学习位置与声压的潜在关联。例如在房间声学场景中，通过墙面、角落等限制区域的传感器数据，可构建全空间声压分布模型。核函数选型：核函数（协方差函数）决定模型对声场空间相关性的捕捉能力，常用径向基核函数（RBF）通过距离衡量位置相似度，适用于平滑变化的声场；多项式核函数则可处理非线性声场特征。核函数参数需结合声场频率特性调整，例如低频声场可增大核函数长度尺度。
FDTD与matlab、python耦合
weixin_51422185的博客
10-08 587
摘要： 本文介绍了使用lumopt-Python API进行逆向设计的入门指南。内容包括如何导入lumopt模块、运行示例模板、项目初始化设置以及优化类介绍。重点说明lumopt可通过CAD脚本编辑器、命令行或Python IDE运行，推荐新手从AppGallery示例入手。文章对比了Lumerical捆绑版与开源版lumopt的区别，并详细介绍了三种基础仿真定义方法：预定义文件、LSF脚本和API调用代码。最后指出形状优化与拓扑优化的主要区别在于几何处理方式。
MATLAB中的while循环：从入门到精通的完整指南
codecrafter123的博客
10-02 628
while循环作为编程中的基础控制结构，在MATLAB中有着广泛的应用场景。从简单的条件重复到复杂的数值算法，它都能够提供灵活而强大的解决方案。掌握while循环的关键在于：理解循环条件的设计、避免无限循环的陷阱、合理使用break和continue、注意性能优化。这些技能不仅能让你写出更高效的代码，也会让你在面对复杂问题时有更多的解决思路。记住，编程就像学习任何技能一样，需要不断练习和思考。下次遇到需要重复执行的任务时，不妨考虑一下while循环是否能够提供更优雅的解决方案。
MATLAB计算有效干旱指数(Effective drought index, EDI)
corn1949的博客
10-05 214
MATLAB计算有效干旱指数(Effective drought index, EDI)
MATLAB Coder代码生成（工业部署）——MATLAB技巧
985工科博士毕业，专攻定位、导航和滤波等算法研究。从业10年，主要使用MATLAB
10-06 1451
通过 MATLAB Coder，可以轻松地将 MATLAB 代码转换为高效的 C/C++ 代码，适用于嵌入式开发、性能优化和实时系统。此示例展示了一个简单的转换过程，实际应用中可以对更复杂的函数进行类似操作。如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者。
MATLAB循环控制：break和continue语句详解
2501_91408482的博客
10-07 520
本文详细介绍了MATLAB中break和continue语句的使用方法与应用场景。break用于立即终止当前循环，适用于找到目标后提前退出的情况；continue则跳过当前迭代进入下一次循环，常用于数据过滤和特殊条件处理。文章通过多个代码示例展示了两种语句在for和while循环中的实际应用，包括嵌套循环中的注意事项。同时提供了性能优化、代码结构优化和调试技巧，并指出了常见陷阱如无限循环问题和多层循环跳出方案。总结指出合理使用这两个语句能使代码更高效清晰，是处理复杂循环逻辑的重要工具。
MATLAB构造10 阶幻方（Strachey 方法）
corn1949的博客
10-04 235
MATLAB构造10 阶幻方（Strachey 方法）
基于MATLAB的物理层算法原型验证
山山的学习笔记
10-03 799
例如，信道估计是物理层中的关键技术之一。基于MATLAB的物理层算法原型验证是一项重要的研究方向，它不仅为通信系统的设计与优化提供了强有力的支持，也为工程师提供了一个高效的工具平台。通过对一个典型的信号调制算法进行优化，我们可以看到，使用MATLAB进行仿真验证后，算法的误码率降低了约30%，有效提高了信号传输的可靠性。尽管MATLAB在物理层算法原型验证中已取得了显著成果，但随着通信技术的不断进步，新的算法和技术层出不穷，如何持续优化MATLAB仿真平台，以适应日益复杂的通信需求，仍然是一个巨大的挑战。
使用matlab进行牛顿迭代求函数极值的方法
haing2019的博客
10-03 1227
本文介绍了一个使用牛顿迭代法（Newton-Raphson Method）求解非线性方程的 MATLAB 例程，通过牛顿迭代法计算得到函数的极值。
【MATLAB技巧】contour|等高线图绘制，使用示例和使用技巧
985工科博士毕业，专攻定位、导航和滤波等算法研究。从业10年，主要使用MATLAB
10-08 1034
示例4: 红色虚线，线宽2colorbar;title('红色虚线等高线 (线宽2) 作者：matlabfilter');快速生成数据：使用peaks函数或meshgrid生成测试数据。生成均匀层级。性能优化：大数据时降低网格分辨率（如peaks(100)改为peaks(50)如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者😊。
MATLAB 九大行星太阳系运行程序
2501_92729044的博客
09-27 584
该MATLAB代码实现了一个太阳系行星轨道模拟系统。代码使用万有引力常数和开普勒定律计算行星运动轨迹，在3D空间中可视化显示太阳和八大行星（包括冥王星）的运行轨道。系统参数包括各行星质量、轨道半长轴、离心率和倾角，以不同颜色区分行星。模拟过程计算每颗行星的轨道周期，通过动画展示100天内的运动轨迹，并自动保存为GIF格式动画文件。代码还包含光照效果、坐标轴标签和行星名称标注等可视化增强功能，完整呈现了太阳系行星的运动规律。
MATLAB信号处理实用指南：从入门到精通
Cyb3rMagnet的博客
10-02 1005
信号，简单来说就是随时间或空间变化的物理量。语音信号（声音的振动）图像信号（光强的分布）生物信号（心电、脑电等）雷达信号（电磁波的反射）信号按照时间特性可以分为连续时间信号和离散时间信号。在计算机处理中，我们主要处理的是采样后的离散信号。MATLAB的信号处理功能主要集中在Signal Processing Toolbox中，这可是个宝藏工具箱啊！信号处理是一个广阔而深奥的领域，本文只是抛砖引玉，介绍了MATLAB信号处理的基础知识和一些实用技巧。
【Sage-Husa自适应 三维EKF】Sage-Husa 自适应扩展卡尔曼滤波在三维非线性系统中的应用，MATLAB代码示例。订阅专栏后可直接查看完整代码
985工科博士毕业，专攻定位、导航和滤波等算法研究。从业10年，主要使用MATLAB
10-06 430
本文展示了Sage-Husa自适应EKF算法在三维非线性系统中的应用效果。通过在线估计过程噪声Q和观测噪声R的协方差矩阵，该算法能有效适应实际环境中的不确定性。仿真结果表明：1）标准EKF和Sage-Husa EKF相比未滤波状态具有明显优势；2）Sage-Husa自适应版本通过遗忘因子（b=0.95）动态调整QR矩阵，进一步提升了滤波精度；3）算法采用特征值分解保证协方差矩阵的正定性（阈值1e-6）。MATLAB代码提供了完整实现，包含三维非线性运动模型和自适应噪声估计模块，可直接运行验证。
算法代码专题７：多元线性最小二乘问题应用实例：房价预测
10-06 739
本文基于波士顿房价数据集，通过多元线性回归模型演示最小二乘法在多因素预测中的应用。选取面积、房间数和房龄三个特征变量，建立房价预测模型。MATLAB实现结果显示回归方程为：房价=127.96+2.15面积+21.99房间数-1.74*房龄，其中房间数影响最显著。模型决定系数R²=0.9497，表明模型具有较强解释力。通过可视化展示了实际房价与预测房价的良好拟合效果，验证了多元线性回归在房价预测中的有效性。
matlab计算算法的运行时间
最新发布
CUMT_DJ的博客
10-08 115
GWO_Convergence_curve 500 次迭代中每次的最优总功率(最后一个值就是best_position)% 修正：根据GWO函数定义，返回值应为 [最优适应度, 最优位置, 收敛曲线]% GWO_best_position 每个节点的最优传输功率配置。% GWO_best_fitness 网络全连通时的最小总传输功率。% 记录GWO运行时间。
Matlab通过GUI实现点云的快速全局配准(FGR)
不枯石的学习笔记
10-01 1721
FGR（快速全局配准）是解决传统ICP算法痛点的点云配准方法，具有无需初始变换、处理快速和鲁棒性强的特点。MATLAB2020a及以上版本通过pcregisterfgr函数实现FGR，流程包括点云预处理、特征提取、匹配优化和配准评估。FGR适用于三维重建、工业检测、自动驾驶和医疗影像等领域。本文还提供了不依赖特定MATLAB版本的FGR实现代码，包括基础版和GUI版，增强了算法的通用性。配准结果虽为粗配准，但为点云处理提供了灵活解决方案。
基于遗传优化的LSTM-Attention一维时间序列预测算法matlab仿真
MATLAB,verilog,python,opencv,tensorflow,caffe,C,C++
10-01 606
本文提出了一种基于遗传算法优化的LSTM-Attention混合模型，用于解决传统LSTM在时间序列预测中存在的超参数依赖经验设置和长序列关键信息挖掘不足的问题。该算法通过Attention机制增强关键时序特征的权重，同时利用遗传算法全局优化模型超参数。实验结果表明，该方法显著提升了预测精度与鲁棒性。文章详细介绍了算法原理、实现步骤和仿真参数设置，并提供了完整的Matlab程序代码（2024b/2022a版本）。该模型特别适用于电力负荷、金融波动等具有复杂时序特征的一维时间序列预测任务。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值