关于线性代数当中的基变换和线性变换这一块,个人觉得特别繁杂,看起来简单,但是推导起来有点混乱,于是写下这篇博客记录一下初次学习的笔记和一些理解。本文参考麻省理工Gilbert Strang的线性代数公开课和戴华老师的《矩阵论》所写,理解有误的地方请大家指出。
学习线性代数可以从很多个地方入手,比如说同济版的《线性代数》从行列式入手(个人觉得很难接受);Mit公开课上的以矩阵的4个子空间入手;据说从线性变换入手也是可以的,所以博主想写的就是一个从线性变换入手的一个思路,在开始之前,大家可以先想象一副完全空白的画面,完全空白。
这个完全空白的画面是一个空间 V,首先往里面放入一个线性变换 T,所谓的线性变换,实际上是一条规则,所以现在我们的空间中仍然是一片空白。这个规则说,有一些变换比较特别(也可以理解成某个函数),它满足:
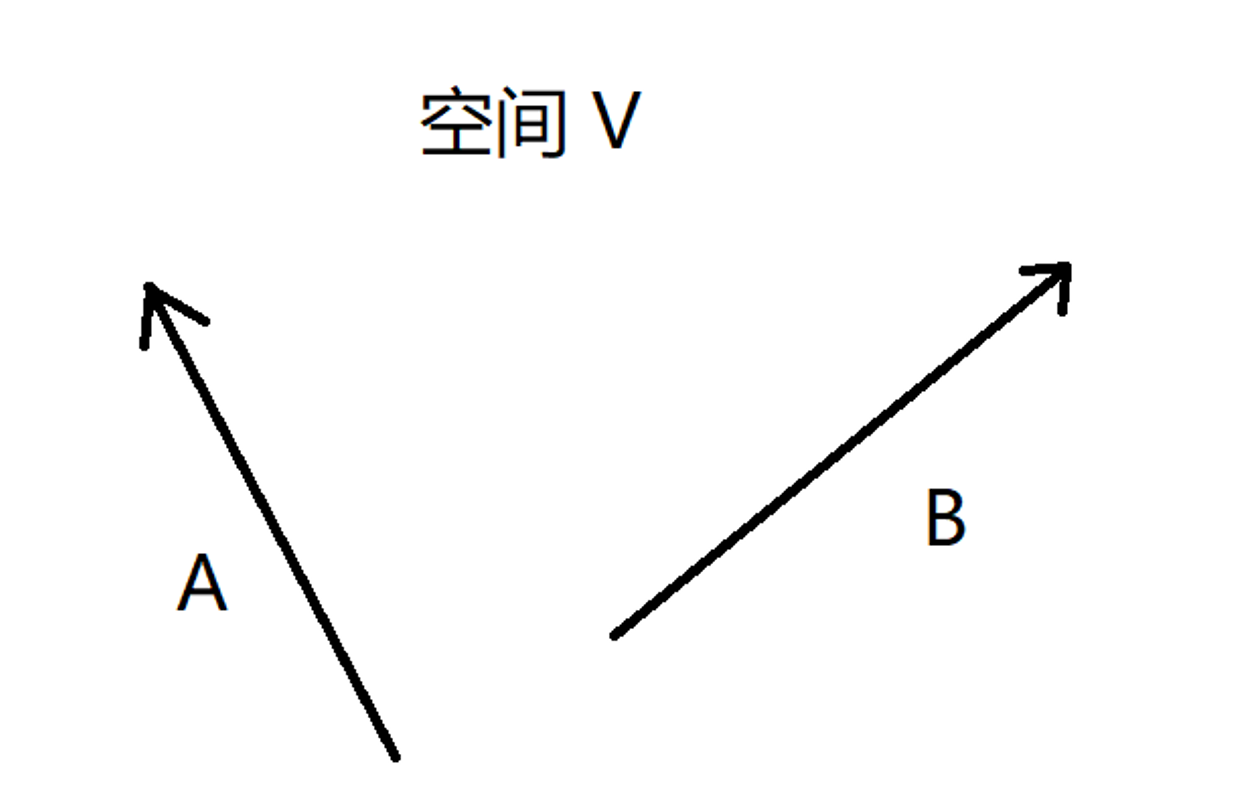
这是一条最基本的规则,非常的重要。下面我们继续来完善这个规则,首先是输入和输出,我们并没有限定输入和输出的维数是什么,所以输入和输出的维数不必相等(千万不要以为线性变换对应的矩阵一定是方阵),比方说 T :R3 -> R2 ,那么在我们的空间 V 中的任意一个3维vector都可以通过 T 变换成一个唯一的2维vector,而且 T 满足上面的规则。注意,现在所说的vector只是一个箭头,它并没有坐标,例如下面的 T(A)= B:
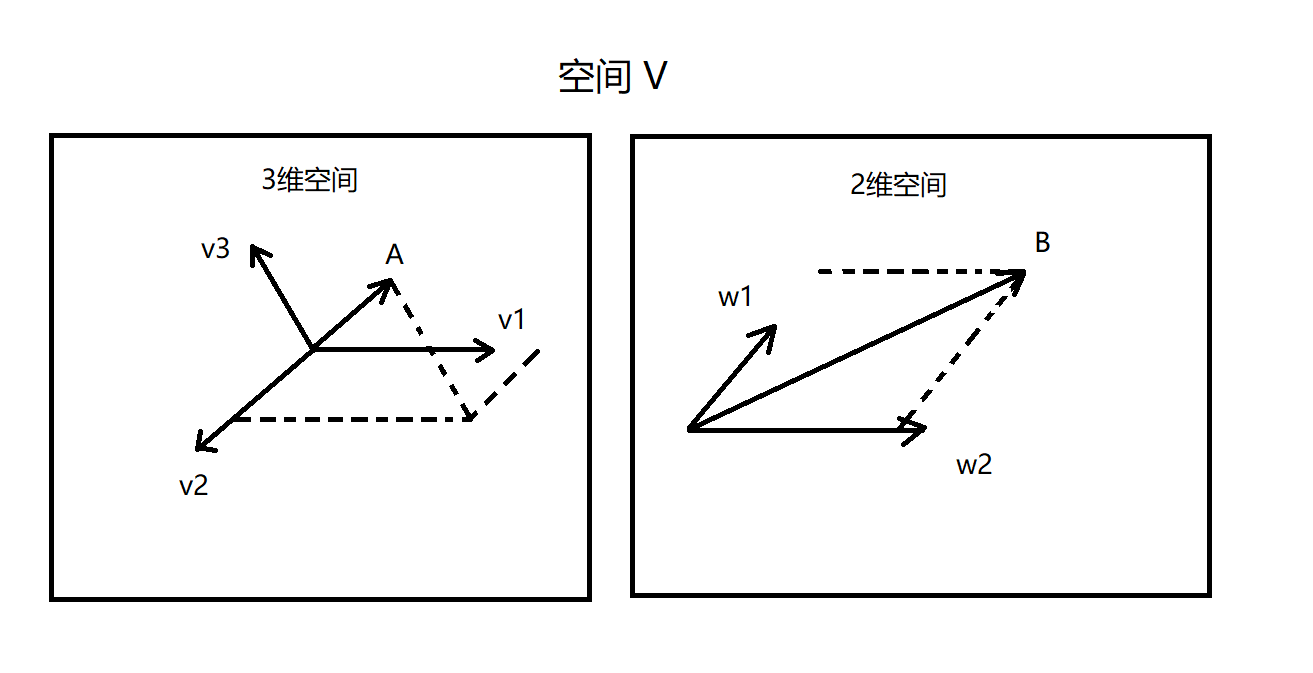
那你可能会问,何来3维和2维的区别呢?这和它没有坐标是一个道理,因为我们还没有指定基。3维说明它有3个线性无关的基向量,2维说明它有2个线性无关的基向量,当我指定了基以后,3维的vector就可以表达成 <a1, a2, a3> ,而2维的vector可以表达成 <b1, b2>了 ,现在我来指定3维空间的基是 (v1, v2, v3),2维空间的基是 (w1, w2),然后当然的在空间 V 中划分出3维空间和2维空间来:
然后你又会问,那坐标得怎么算呢?这里可以这么理解,提供基的目的是提供一个基准,我们得同时给定一个方向和一个单位长度,这好比我指定了地图上的东和北是右和上两个方向,指定111千米是1度,这才可以用 <a, b> ,也就是经纬度来定位地球上的每一个点。OK,那我们就这么来办,我指定各个维度的方向就是各个基向量








 本文详细梳理了线性代数中的基变换和线性变换概念,通过麻省理工的线性代数课程和矩阵论的理解,阐述了线性变换的规则、坐标变换的重要性,以及如何通过基来描述变换。内容包括线性变换的定义、输入输出维数、坐标计算、矩阵表示以及特征值和特征向量的探讨,旨在帮助读者理解变换的内在逻辑。
本文详细梳理了线性代数中的基变换和线性变换概念,通过麻省理工的线性代数课程和矩阵论的理解,阐述了线性变换的规则、坐标变换的重要性,以及如何通过基来描述变换。内容包括线性变换的定义、输入输出维数、坐标计算、矩阵表示以及特征值和特征向量的探讨,旨在帮助读者理解变换的内在逻辑。
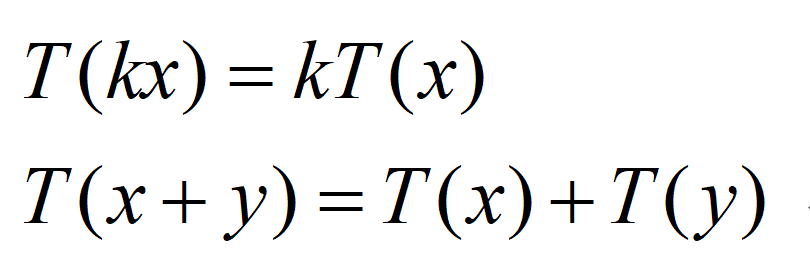
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 2965
2965

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








