线性代数基础14--线性变换与基变换

1,线性变换

将一个R2向量变换为一个R2向量.就是投影做的事.
并不依赖坐标轴进行变换.
满足以下性质

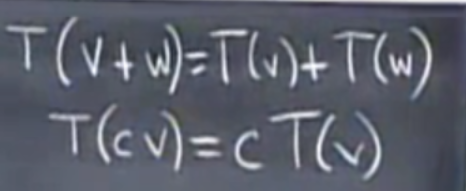
就可以叫线性变换,投影就是一种线性变换.
并且在线性变换中T(0)=0

例二

向量修正,对于向量V加上某一修正向量,得到新的向量.
向量修正不满足两条性质,并且T(0)也不等于0,所以不是一个线性变换.

例三

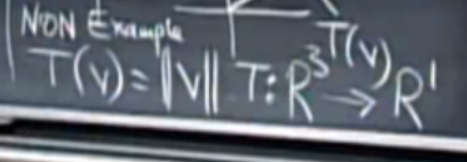
一个向量求模,对于负的数乘不成立,对于加法也不成立.如-1×v结果应该为v的模长的负数,但是并不是.所以也不是一个线性变换.

例四
旋转

左边为输入,右边为输出,也并不依赖坐标系,去掉坐标系也可以描述该变换.
这也是一个线性变换.

例五
矩阵乘法也满足线性变换的条件.

通过乘以一个矩阵,整个平面内的向量都可以完成一种变换.
这里也就引出了旋转矩阵等概念.

如上图,如果矩阵A如上,起到的作用是,x向量不变,y向量取反,所以输入整个房子的向量都变化了.

我们如何理解一个线性变换?
就是理解其背后的矩阵,为了确定矩阵,虽然线性变换不依赖坐标系,但还是要引入坐标系确定矩阵.

如果矩阵A可以实现R3到R2的映射,那么A就应该是2×3的矩阵.

我们如果想要了解线性变换对空间的作用,不需要知道其对每个向量的作用,只需要知道线性变换对一组基的作用,因为其他向量都是这组基的线性组合.

那么如何将线性变换与坐标联系起来呢?
一旦确定了一组基,那么对于向量来说,C1,C2等等就是他们的坐标值.我们的平面直角坐标系也就是选择两个基建立的.

什么是坐标?

上图中(3,2,4)就是坐标,所以(1,0,0)(0,1,0),(0,0,1)才被叫做标准基.


这里要注意基选择的是V1,V2而不是标准基,之前的投影矩阵那么麻烦,也就是选择标准正交基所致.可以看到选用v1,v2的A矩阵非常简单.

并且在本例中由于取了投影的特例,所以A刚好是对角阵,基也刚好就是特征向量.

所以在这个例子中特征向量组成的基是最好的.

这是更一般的得到A矩阵的办法.


这里尤其是第二条为什么(1,0,…,0)是基向量,因为这个坐标表示的就是基的线性组合,所以这个乘以第一个基就等于第一个基.这样就得到T(v1)=a11w1+a12w2+…也就是A矩阵的第一列,这样来确定A,这种方法需要我们预先知道输入与输出.
如上面的两个例子中,我们都知道每个输入对应的每个输出.

2,基变换与图像压缩

来看我们日常中的一张图片,一般由512×512个像素组成.其中如果是黑白图片,每一个像素占据8比特的空间(彩色图片RGB扩大三倍为24比特).在线性代数中,研究图片,其实研究的就是(512)平方维空间.
我们的每一个像素都是1个基,所以整个向量就(512)平方这么长.

如上就是一组标准基,每一个1代表一个像素,这有一个问题就是,没有考虑像素之间的相关性.如整块黑板都是黑色,也需要用这么多像素表示.

这可能是一组更好的基

现在JPEG压缩方法用的基为傅里叶基,就是将傅里叶矩阵拆开

对于该压缩方法一般把512×512的图片分割成8×8的小块进行压缩.根据上一节我们知道一副图片进行基变换会得到变换后的坐标,然后乘以对应基组成变换后向量.所以我们第一步得到64个参数
第二步进行压缩,可以设置阈值,将人眼分辨不出的太小的参数去掉.(这一步产生损失)
第三步我们得到去掉一部分参数的c,可能是20,15…,然后乘以傅里叶基构成变换后向量.

但是对于视频来说,有些视频的前一张图片与后一张图片拥有很强的相关性.

另外除了傅里叶基还有一种基也很好用,就是小波变换.

如上为R8空间中小波变换的八个基,后面省略的三个是第三四位置上为1,-1,依次往下.

我们在基变换步骤中要做的事情是什么?

就是将标准基下的坐标P(这里取8个像素点,所以是R8)表示成小波变换基的线性组合.得到这些C

这里W为8个小波基组成的.小波变换的这组基最大的特点就是相互正交.所以说W矩阵的逆就是W的转置.

并且还有第二点,基的性质是否好,就是在做数据压缩的时候,不能丢掉太多的信息,少量基就可以概括图片,不然图片会变黑.
看到上面的方程很容易会想到上一节学到的线性变换.在上一节,我们将标准基(1,0,0,0…)乘以线性变换矩阵A,得到A的第一列就是用另一个空间基表示这个标准基的线性组合.那么是否上一节的A矩阵就是这里的W逆矩阵?
这里经过自己的计算是这样的.
并且从新的基变换回标准基的A矩阵就是W.
这里需要注意,从新的基变换回标准基与从标准基变到新基是不同的线性变换,而下图的定理是针对于同一种线性变换存在的关系.

对于同一个线性变换,变换矩阵A,B之间是相似的,如旋转,等