Wasserstein距离的直观解释

Wasserstein(EM)距离的易懂解释

最近在学习Wgan相关知识时，看到wasserstein距离的相关数学概念，表示非常懵逼，结合着李宏毅教授的网课，觉得理解了一点，但是还是不透彻，于是乎重新拾起概率论课本，仔细研究了一番，有以下直观的认识。

1.Wasserstein（Earth Move）距离的直观理解

1 P和Q的分布示意图。

所谓EM距离，就是衡量两个分部之间的差异的一种计算方法。即把一个分布变换成另外一个分布需要的能量。（老板要给建筑工人搞建筑发的工资）接下来我将通过一个小例子详细解释一下它。

假设现在有两个分布，P和Q。

P的横轴为xp ，而Q的横轴为 xq 。纵轴表示在此横坐标上的y值。说了这么多，比较晦涩，我用一种直观的语言来描述一下。

P：大家好我是一堆砖头，长得像上图P的样子一样。
Q：大家好，我是一个房子（长得真草率）的设计图，P那堆砖头想变成我的样子。

好了，现在改如何把这堆砖头变成Q的样子呢？

（1）搬砖

我们可以这么做：

2 搬砖示意图，图中的一些文字我会在下面的“算账中进行解释”

如figure2所示，首先我们看两个轴，他们分别是xp 和xq ，其坐标和figure1一致，可以看到，Q的分布已经被我画成了虚线框，

虚线代表什么呢？他代表现在Q这个地方没有任何东西，只是一张设计图，我现在要做的，就是把P这堆砖头移动到这个虚线框里面。

接下来，我举例一种移动方法咯：

如figure2所示。已经被我打上了格子，每个格子的坐标都可以用xp 和xq 表示出来，比如说左上角的格子，它的坐标就是xp =1和xq=1，即（1,1）；依次类推，其他格子的坐标也就可以知道了，右下角的格子坐标是（4,4）。

那么，格子里的数是什么呢？就是P要往Q对应位置移动砖头的个数！

举例，看（1,1）格子，里面红色的3就代表把P这堆砖头的xp =1处的3块砖头一起移动到Q设计图框架的xq=1处。 此时，Q的xq=1处的砖头还差一块。所以，我把P的xp =2处的一块紫色砖也移到了Q的xq=1处。于是乎Q设计图的xq=1位置已经搭建好了。

还是看上图，依次类推，我们可以按照同样的方法填充格子里的数字，最终结果就和figure2一样了！通过我们打工人的努力，所有的P砖头都被搬走了，并且形成了我们Q设计图里长得样子耶！

我们细心的观察，还会发现，表格里的数字，横着加起来是P对应位置的砖头数；纵着加起来就是Q对应位置的砖头数！（这好像没有什么好惊喜的，本来砖头就是这么搬的，所以加起来肯定是这样咯）

目前为止，我们的砖头已经搬完了，下一步就是算账了！

（2）工资

优秀的打工人已经把砖搬完了，建筑成了我们想要的Q的样子。现在好像缺点什么事情唉，要发工资！对，我们就是一个资本家，要给打工人发工资，唉，来算算工钱吧！

可以看到figure2中，我写了一个γ \gammaγ ,这个γ \gammaγ 是什么？他代表我们作为老板的一种策略：小李，你把这个搬到那！小王，你搬这个。。。具体到图上而言，就是我们的这个4x4的格子以及里面的数。它代表了我给打工人安排的搬砖的策略。

话不多说，上算账的公式！
$B(\gamma )={\sum }_{x_p,x_q}^n\gamma (x_p,x_q)||x_p-x_q||公式（1）$

好了，我们来看这个公式在说什么哈：

3 工资计算过程

我们已经看到我这个黑心老板安排的搬砖策略了，就是figure2里面的那个4x4的表格。它就叫做 $\gamma$ ,对于这个策略，我们要发的工资就是$B(\gamma )$：

这个工资怎么算！就是按照公式1算，

很明显：
$\gamma (x_p,x_q)$
这一项，就是从表里面的对应坐标去找搬砖的块数。如
$\gamma (1,1)$
就是表里的左上角嘛，就是3！
$||x_p-x_q||$
这一项就更明显了，就是两个横坐标的差的绝对值吗，比如还拿
$\gamma (1,1)$
举例，他这项，就是$|1-1|=0$。

求和，就是把表里面的16个格子都按照公式算一遍，计算过程看figure3。

经过详细的计算：我们算出工资=4！（好低啊，赚了赚了）看来我是一个精明的老板，懂得如何克扣下属哈哈哈。

我惊奇的发现，对角线上的工资，是不用发的！高兴，因为这堆砖头啊，xp=xq相当于本来就在这里，所以小王不费一点力气，就看了他们一眼，他们就算搬过去了咯。这我当然不能发工资了！

所以，按照目前的这个γ \gammaγ 表格，我们的工资已经算出来了。当然，我是一个聪明的老板，还有些不太聪明的老板。他们的策略可能是这样的！

4 不太聪明的老板的搬砖策略

这个老板就显然有点不太聪明的样子了。他让员工把原来都不需要动的砖头搬到了别的地方去。最终造成了劳动力的浪费，我们算出来最后他要发10块钱工资！他完成这个任务付出了我2.5倍的资金。。。

还有很多其他老板，他们也有不同的搬砖策略$\gamma 1$ $\gamma 2$ $\gamma 3$ …要发不同的工资$B(\gamma 1)$ $B(\gamma 2)$ $B(\gamma 3)$…

（3）Wasserstein距离（EM距离）

所谓的EM距离，我们可以理解为诸多老板中，最聪明老板想出的搬砖策略对应的工资。
$W(P,Q)=mi{n}_{\gamma ϵ\Pi }B(\gamma )$ (公式2)

这里的这个$\Pi$就是指所有的老板想出来的所有的搬砖策略$\gamma 1$ $\gamma 2$ $\gamma 3$…

这些策略构成的集合就是$\Pi$，而Wasserstein距离，就是从这些策略里面找到工资最少的那个策略对应的工资，如果拿上面的figure2来举例 ，那么很可能，这个$W(P,Q)$就是4。我就觉得我是最聪明的老板略略略。

2.把Wasserstein距离普遍化

（1）公式的解释

听我扯了这么多搬砖的理论，你一定累了，感觉我这个人太low，太粗俗。好了，我们来看看wgan这个论文里面，作者写的Wasserstein距离的公式是什么吧！
$W(P,Q)=in{f}_{\gamma ϵ\Pi (P,Q)}{E}_{(x,y)\sim \gamma }[||x-y||]$

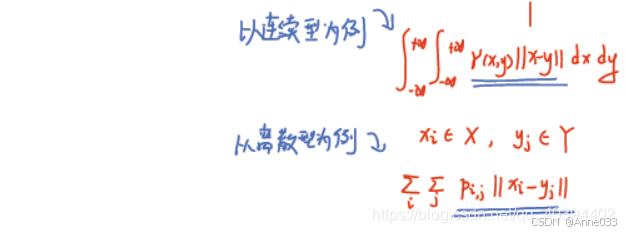
5 解释书面版本的Wasserstain距离

看上图的文字，$\gamma$仍然是指一个策略，比如搬砖，就是那个表格。而其他情况，分布是很复杂的，这个策略并不是一个表格这么简单。而$\Pi (P,Q)$还是指把P转换成Q的所有策略，还是可以理解为所有的搬砖方法，即所有的$\gamma$。

现在这个$\gamma$复杂一点可以叫做，联合分布，简单一点就是我们上面说的那个表格。后面的期望是什么意思呢？

我们知道，期望分为连续型分布的期望，和离散型分布的期望，看上图，我已经写了出来该怎么去求这个期望。对于连续就是求二重积分，离散就是二重求和。

多说无益，我来举个例子，就拿离散型的二维联合分布来举例子吧！看看用论文里的公式该怎么求这个Wasserstein距离！

（2）对某个离散型联合分布gamma的期望计算

我把figure4那个不太聪明的老板的策略引来了，他现在就是策略$\gamma$也可以叫做联合分布$\gamma$。

既然是联合分布，那么联合分布里面的数值就应该是概率。那么怎么把搬砖数改成概率呢？这好说，总共有10块砖，那么概率就是砖块数目/10。

所以，我们那个不太聪明的老板的搬砖策略就变成了一个二维联合分布$\gamma (x_p,x_q)$ 。有两个变量，分别是$x_p,x_q$，你就把他们当成概率论书上写的x，y就行了。

表格里的转块数全部除以10 ，填到表里面。现在，这个表就变成了一个完美的二维离散型联合分布了。我们把两边再补上两列，如figure6红色的线所示，每一行加起来，刚好就是P对应位置的砖头数目/10;每一列加起来，刚好就是Q对应位置的砖头数目/10。（等等，这个结论好像似曾相识哎）。我们再想一下，这不就是概率论里面讲的边缘分布吗！再看看，不就是P和Q的分布吗！

所以就是说，每一个联合分布$\gamma$的边缘分布都是P和Q。无论你的联合分布长成什么样子，它的边缘分布一定是P和Q。

6 解释离散型联合分布的EM距离求法

好了，按照论文里的公式，我可以算一下这个联合分布γ \gammaγ 他的期望咯，算出来是1.0。

回去看一眼figure4，不太聪明的老板他的工资是10，这个期望就是10/砖头总数10=1.0。
$E_{(x,y)\sim \gamma }[||x-y||]$

7 按照面公式计算一个二维离散联合分布的Wasserstain距离

依次类推，我这个聪明的老板，归纳出的联合分布的期望应该是4/10=0.4吧！

（3）Wasserstein公式到底算出的是什么

刚才我举例的γ \gammaγ是那个不太聪明的老板提出的一个二维联合分布是吧。别忘了，我还是一个贪心的聪明老板呢！按我的方法，期望是0.4啊！比1要小很多。当然还有很多老板提出了很多二维联合分布啊$\gamma 1,\gamma 2,\gamma 3$…他们都能算出一个期望来。我还是觉得，我的期望最小了，那么把这么些个$\gamma 1,\gamma 2,\gamma 3$… 他们的期望都算一算，从里面挑出一个最好的$\gamma$ ,它对应的期望，就是Wasserstein距离！

我可以很自信的告诉你，这个例子里，Wasserstein距离就是 0.4！没错，就是我的这个二维联合分布对应的期望啦啦。

3.总结

综上所述，Wasserstein距离其实就是：把一个分布P变换到另一个分布Q，这么多种联合分布($\gamma 1$ $\gamma 2$ $\gamma 3$…)里面，可以使$E_{(x,y)\sim \gamma }[||x-y||]$，最小的那个期望值。

我bb完了，懂得都懂。

————————————————

原文链接：https://blog.csdn.net/qq_40394402/article/details/109565803

最优传输Optimal Transport-Wasserstien距离 以及Gromov-Wasserstien距离以及fused Grosserstien距离

最优传输及其变种算法
一、 最优传输 Optimal Transport & Wasserstien Distance
二、Gromov-Wasserstien Distance
三、Fused Gromov-Wasserstien Distance
四、三个距离的比较例子
说实话我对此理解的也不是太深刻，因为总感觉这个OT算法实在是有些抽象，所以欢迎各位看官多向我提问，我们互相交流以加深理解。

部分参考来源：
Subgraph Matching via Fused Gromov-Wasserstein Distance
Optimal Transport入门简述

一、 最优传输 Optimal Transport & Wasserstien Distance

下面讲讲我理解的内容：

有这么一个情景：我们有很多 n 堆沙子(即我们有一个一维向量 [n, ]), 每一堆沙子重$P^{(i)}\in {\mathbb{R}}^n$，有 m 个坑(即我们有一个一维向量 [m, ])，每个坑能装$Q^{(i)}\in {\mathbb{R}}^m$ 沙子，我们想将这些沙子移到这些坑里，每堆沙子怎么移动才能让代价最小(即解最优)?

我们先来定义一下我们移动沙子要付出的代价，这是一个代价矩阵$M\in {\mathbb{R}}_{>=0}^{n\times m}$，shape为$n\times m$， 描绘了 n 中任一沙堆向 m 个坑中任一坑搬运所要付出的代价，并且里面的数值必须是大于等于0的。

然后我们定义下我们的解矩阵，解矩阵长这样：$T\in {\mathbb{R}}_{>=0}^{n\times m}$ ，描述了从 每个沙堆向每个沙坑搬运多少质量(mass)沙子(所以你可以看出这有很多最优解(话说是局部解吗？))

然后定义将 T 和 M 逐元素相乘（注意不是矩阵点乘）表示总的运输成本，再将所有积求和计算总代价，公式如下:

$Wasserstien-distance=\text{argmin}{\sum }_{i,j}{T}_{i,j}{M}_{i,j}=mi{n}_{T\in \tau (p,q)}⟨T,M{⟩}_F$

并且满足以下约束：

τ ( p , q ) = { T ∈ R + n × m ∣ T 1 m = P , T T 1 n = Q } ; T ≥ 0 \tau(p, q) = \{T\in \mathbb{R}^{n\times m}_{+}|T1_{m}=P, \quad T^{T}1_{n}=Q\}; \quad T \geq 0 τ(p,q)={T∈R+n×m​∣T1m​=P,TT1n​=Q};T≥0

这里的1是一个全 1 的向量(矩阵)，P和Q我们又称为分布，在实际计算中因为不易获得，我们一般直接设定为统一分布(uniform)

总的代价我们称为 Wasserstien-distance， 这个距离越小表示这两个数据越接近。 T 矩阵就是我们想求解的运输矩阵，它描述了任一沙堆向任一坑搬运多重的沙子是代价最小的（最优的）。

二、Gromov-Wasserstien Distance

上部分说的wasserstien距离有一个缺陷，那就是如果两个分布之间并没有直接关系（专业说法叫不在同一个空间），我们是很难获得两个分布之间的代价矩阵 M 的。上边这个例子是讲的搬运沙子，那么无论沙堆还是沙坑，直接的关系就是都使用沙子的重量来衡量，而如果两个分布间没有直接的关系，或者代价矩阵及其难求解，由此引出Gromov-Wasserstien Distance。

这个算法的思想是这样的：有这么两个不同空间$A\in {\mathbb{R}}^n$和 $B\in {\mathbb{R}}^m$， 我们计算从 $A_i$到 $A_j$之间的距离，即对于整个A空间的各个点，计算它到其他点的距离，我们就可以获得一个内部的代价矩阵$C^A\in {\mathbb{R}}^{n\times n}$， 对 B 同理可得$C^B\in {\mathbb{R}}^{m\times m}$ , 既然我们不能直接在两个不同空间之间建立联系(无法轻易获得代价矩阵)，那我们就比较两个空间中成对距离的差异（由此也可以看出GW算法只关注空间的图形结构而不关注空间内各点的属性）。

用$C_{i,i^{\prime }}^A$表示A空间从点 i 到 i‘ 的距离，那么我们就可以使用一个损失函数(Loss Function)来评估$C_{i,i^{\prime }}^A$与$C_{j,j^{\prime }}^B$的不同，我们因此可以定义一个张量：

$L_{i,i^{\prime },j,j^{\prime }}=\mathcal{L}(C_{i,i^{\prime }}^A,C_{j,j^{\prime }}^B)\in {\mathbb{R}}^{n\times n\times m\times m}$然后我们定义传输矩阵$T_{i,j}$ 和$T_{i^{\prime },j^{\prime }}$表示从点 i 到 j 和 从 i’ 到 j’ 所要移动的质量(mass), 其中 (i, j) 是A空间的，(i‘, j’) 是B空间的。然后${\mu }_A$ 和 ${\mu }_B$表示A、B空间的离散概率观测， p q表示其概率向量，通常也是用 uniform distribution.

最后我们就可以表示出 GW distance:

$GW(p,q,C^A,C^B)=mi{n}_{T\in \tau (p,q)}\sum \mathcal{L}(C_{i,i^{\prime }}^A,C_{j,j^{\prime }}^B)T_{i,j}{T}_{i^{\prime },j^{\prime }}$

三、Fused Gromov-Wasserstien Distance

最后就是介绍 Fused Gromov-Wasserstien（FGW） Distance，原理非常简单，就是结合了wasserstien距离和GW距离，感觉像是缝合怪哈哈

公式如下：

$lFGW(p,q,M,C^A,C^B)=mi{n}_{T\in \tau (p,q)}(1-\alpha )⟨T,M{⟩}_F+\alpha \mathcal{L}(C_{i,k}^A,C_{j,l}^B)T_{i,j}{T}_{k,l}$

可以通过调节 α \alphaα 来改变两个距离的占比，FGW的缺点和wasserstien类似，需要寻找 两个空间的代价矩阵 M。

四、三个距离的比较例子

有如下两个图：

各种代价矩阵如下：

计算出的三个算法的传输矩阵和转换结果：

虚线越深表示两个节点间的连接越深，上图深虚线表示 1/3的mass，浅的表示 1/6的mass

上图可以看出GW仅关注两个图的几何结构而不关心节点的属性，另外wasserstien仅考虑特征，FGW则可以同时考虑两者

————————————————

原文链接：https://blog.csdn.net/potato_uncle/article/details/136181036