3D场景中的逆运动学介绍

翻译自https://www.alanzucconi.com/2020/09/14/inverse-kinematics-in-3d/
参考阅读 2D场景中的逆运动学
逆运动学 inverse kinematics
正向运动学：根据角A和角B，计算执行器末端的位置
逆运动学/反向运动学：根据执行器末端的位置，推算出角A和角B

介绍

事实是，逆运动学是一个不仅在电子游戏中反复出现的问题，而且在工程和科学领域都是如此。从机械臂的设计到对人脑运动控制的理解，各种形式的逆运动学起着重要作用。

简介

2D场景中的逆运动学。
如下图所示，是一个约束在二维平面中的双关节臂。两个关节点分别由角度A和B控制。通过调节这两个角度，称为末端执行器（ end effector）的机械臂尖端将到达不同的位置。机械臂尖端（the tip of the robotic arm）是角度A控制的关节点

逆运动学的问题是找到角度A和B，以便末端执行器到达所需的目标点。下面的动画显示了一个机械臂正在XY平面上画圆。

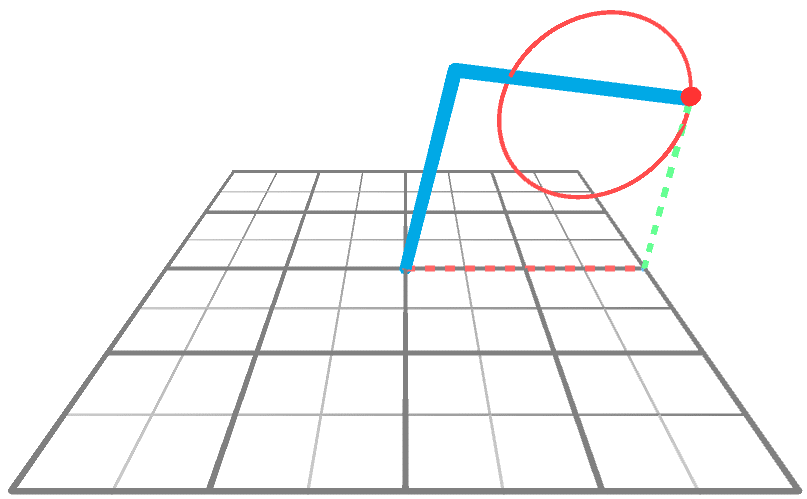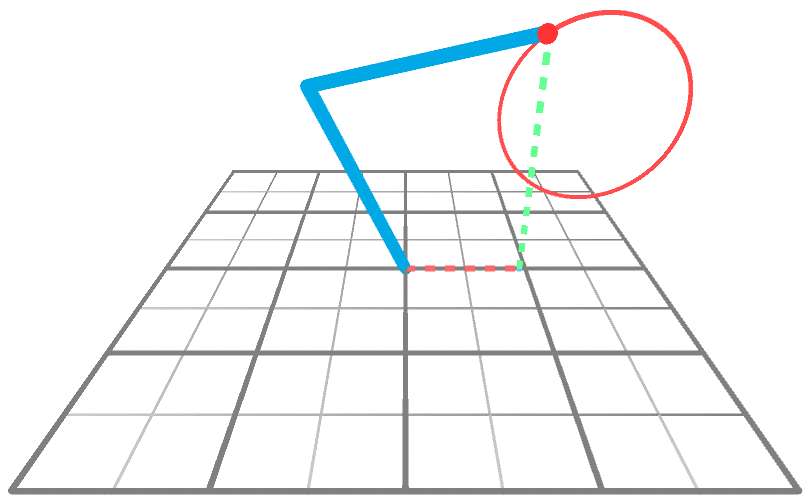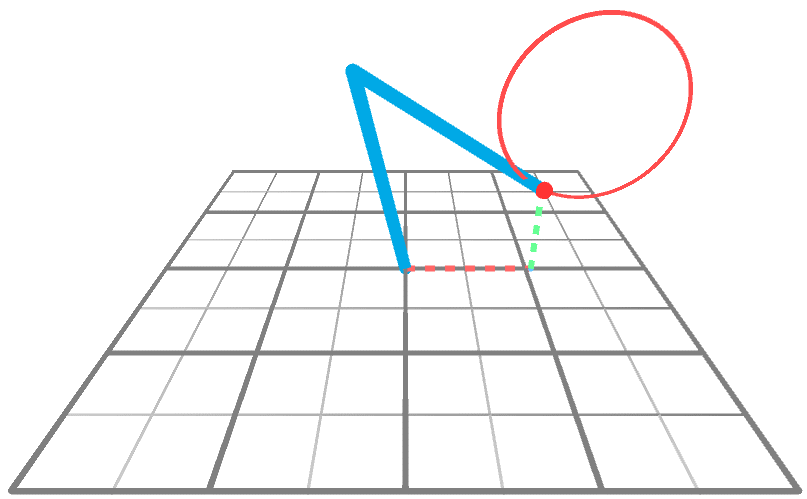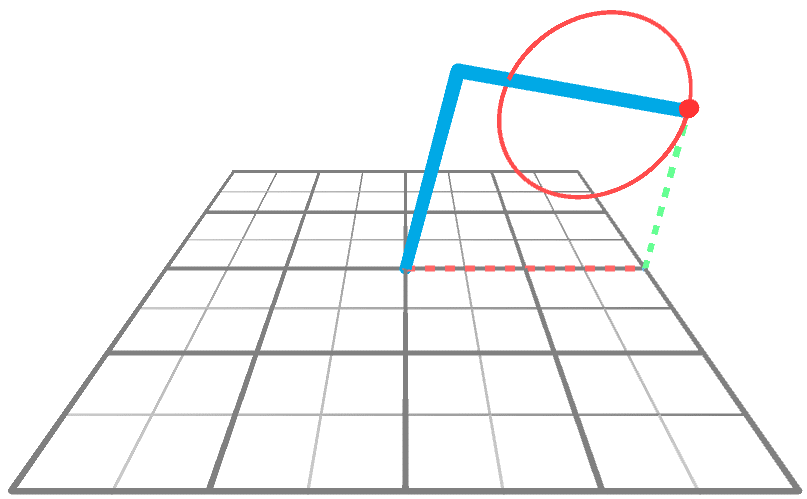
我们可以将机械臂想象成一个三角形（下图），有两个内角$\alpha$和$\beta$。

根据三角余弦定理，可得

那么

根据反正切函数求得

延伸到三维空间

首先，我们需要了解，2D中有两个关节手臂的场景是一个具有两个自由度（2 degrees of freedom, 2DOF）的问题。与人们想象的可能不同，这表达的不是机械臂有两段；而是我们可以控制两个变量（在这种情况下，是关节的角度，角A和角B）。
当我们把这个问题扩展到三维空间时，我们的机械臂仍然有两个段和两个关节。然而，如果我们假设手臂也可以绕第一个关节自由旋转，那么问题现在有三个自由度（3DOF）。
在这种新情况下，第二个接头（B）保持不变。然而，我们假设第一个（A）现在可以在另一个维度自由旋转。因此，第一个关节通常被称为髋关节（hip），第二个关节被称为膝关节（knee）。你的膝盖通常只有一个自由度（向前/向后），而你的臀部有两个自由度（向前/向后和向内/向外）。髋部旋转的角度$\theta$表示。
我们可以想象一个机械臂，其中两个关节可以有两个自由度，总共四个。此时的问题是，将有多种解决方案，使我们的方法不再有效。“腿状”机械臂（“Leg-like” robotic arms，意思是：有髋关节和膝关节的手臂）在游戏和整个行业中都很常见。所以这种方法可能值得研究。
如果你读过之前的文章，你可能会记得，如果目标在2D中是可到达的，那么总是有两个“镜面反射”解决方案（见下文）。

同样的问题也出现在3D中；这一次，解决方案是无限的。这是因为配置可以围绕由连接原点和目标的直线表示的对称轴旋转。解决方案是…只关注一个解决方案！在本教程中，我们将重点介绍最简单的查找方法，它假定（0，1，0）为“向上”方向

从二维到三维

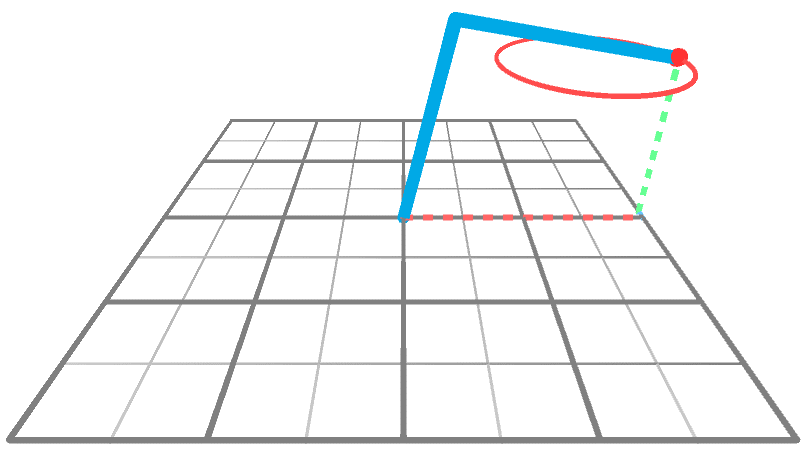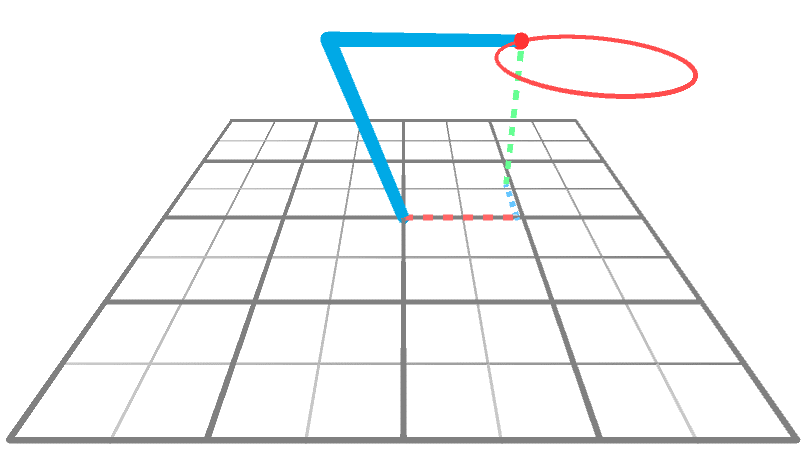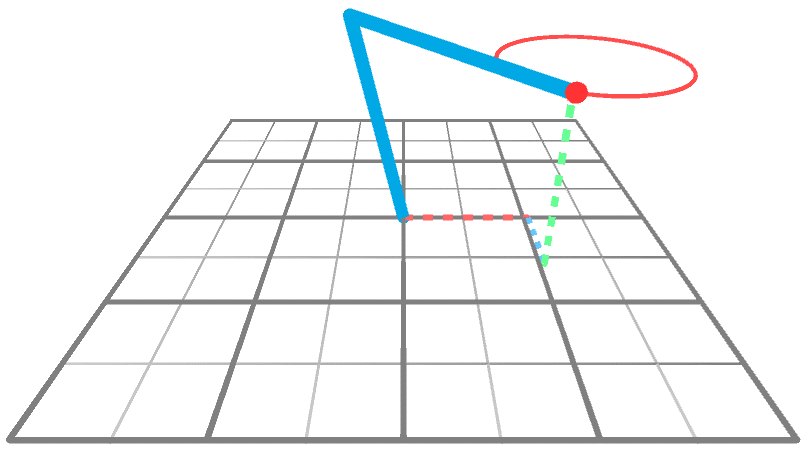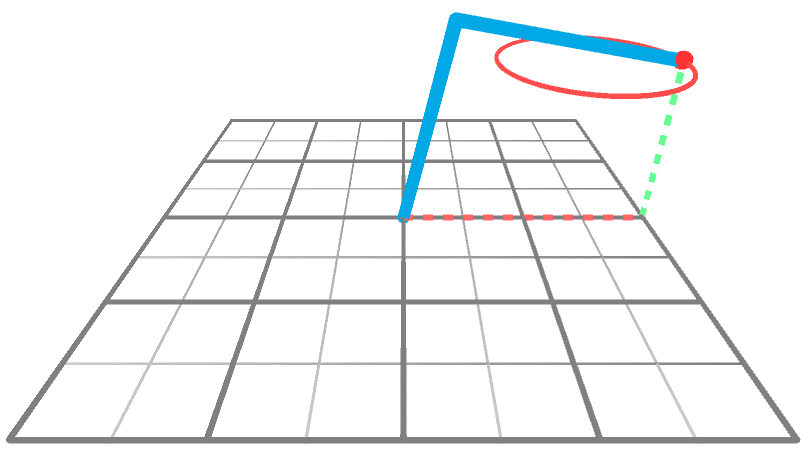
到目前为止，我们只知道当运动被约束到XY平面时，如何求解逆运动学问题。从2D到3D的诀窍是重复使用2D解决方案。下面的动画显示了一个机械臂在3D空间中到达一个围绕Y轴旋转的点。很明显，手臂做的唯一事情就是旋转；它的角度A和B没有改变，只有θ改变。

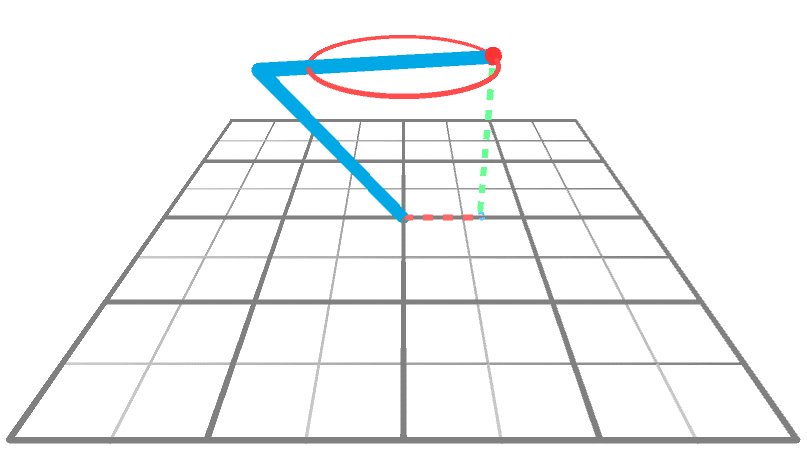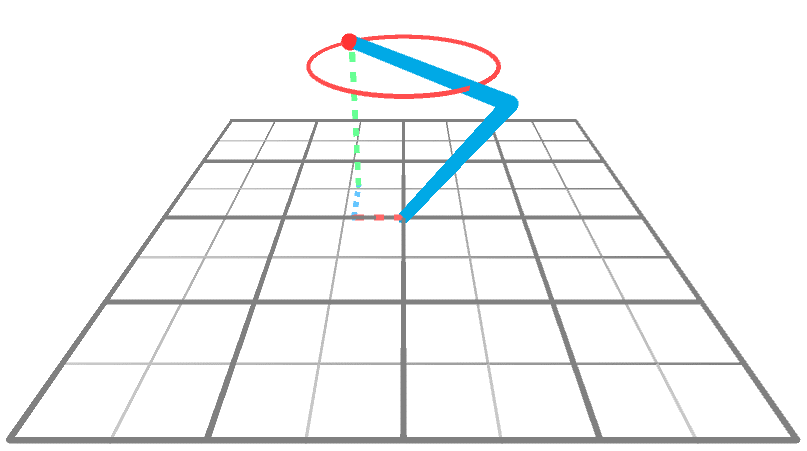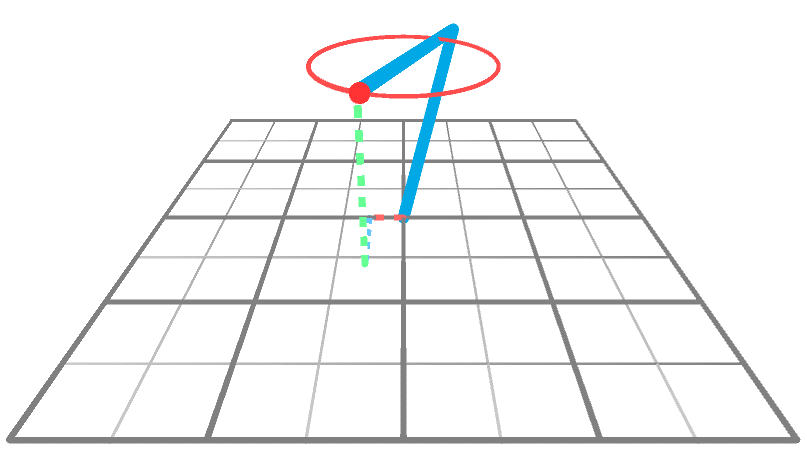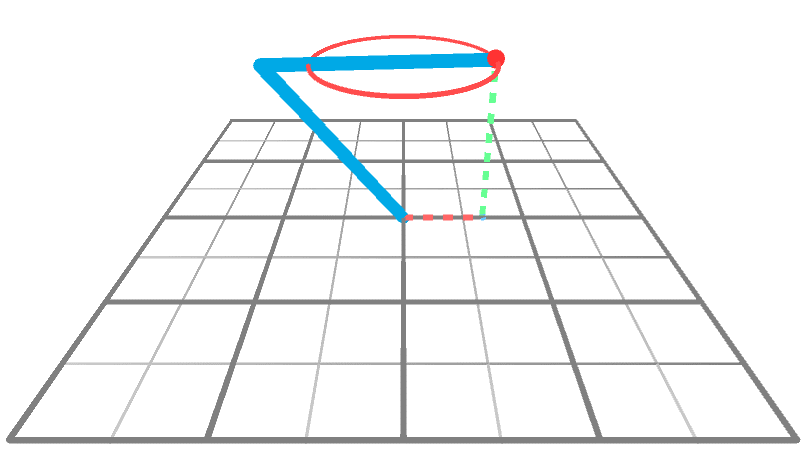
这意味着，如果我们知道如何在XY平面上执行IK（我们知道！），就可以知道如何通过两个简单的旋转在整个XYZ空间上执行IK。从概念上讲，我们可以通过三个步骤来解决这个问题：

1. 围绕Y轴旋转目标点，直到其位于XY平面上
2. 移动机械臂，使其能够到达该点，就像在2D中一样
3. 通过在Y轴上以相反方向旋转整个机械臂来“撤消”旋转

我们可以通过简单地执行二维逆运动学，而不是在XY平面上，而是在从机械臂根部到目标点的垂直平面上，来更有效地实现这一点。

绕Y轴旋转

要在3D中执行反向运动学，我们首先需要计算θ，它是整个机械臂旋转的角度。这是髋关节增加的额外自由度。
找到它的最佳方法是假设机械臂已经到达该位置（意味着C已经在目标位置），并计算得到的角度θ。由于θ是髋关节绕Y轴形成的角度，我们可以直接从顶部观察机械臂。在XZ平面（下图）上方的俯视图中，机械臂看起来像一条直线。这是因为，除了髋关节，其他两个关节是平面上的约束。

如果我们将线段$AC$视为直角三角形的假设，我们可以使用一些三角学来计算角度θ：

WY平面上的逆运动学

从技术上讲，知道θ就足以解决三维逆运动学问题。实际上，我们可以做的是遵循上一节中介绍的算法：围绕Y轴将目标点旋转$-\theta$度，在XY平面上执行逆运动学，最后将整个手臂旋转$+\theta$度。
更快的版本是不在2D平面上执行反向运动学，而是直接在穿过髋关节和目标点的垂直平面上执行反向运动学。不幸的是，有些事情正阻止我们这样做。让我们再次看一看示意图，它显示了所使用的所有角度：

为了计算A，即控制第一个关节的角度，我们需要计算A’。这是第一个关节和目标点之间的角度，如果我们回忆一下用于计算A’的方程式（5），我们会注意到一个大问题：它假设所有点都位于XY平面上

在我们的3D场景中，不幸的是，机械臂会绕Y轴旋转θ度。然而，如果我们与机械臂一起旋转视图，新的图表基本保持不变。我们称之为新的参考坐标系WY，因为X轴现在被W取代，W是X轴，不绕Y轴旋转θ度。

我们不能简单地做$Dx-Ax$，就像我们对$\Delta y$做的那样。这是因为C和D在y轴上对齐，而A和D不在X轴上对齐。它们与W轴对齐。因此，计算$\Delta w$的最佳方法是获得从A到D的距离。这失去了$\Delta w$的正负符号，但幸运的是，它在我们的计算中没有真正的问题。如果你的手臂恰好朝相反的方向移动，只需在代码中翻转$\Delta w$符号即可。

其中$\left|\overline{AD}\right|$是从A到D的段的长度。或者你也可以直接使用毕达哥拉斯定理(Pythagoras’ theorem)

在上面的等式中，毕达哥拉斯定理的Y贡献抵消了它本身，因为点D具有A的相同Y分量，所以它们的$\Delta y$为零

现在，我们真的有了所有东西，可以在3D中对带有一个膝关节和髋关节的机械臂执行反向运动学：