深度学习——第一篇补充（反向传播算法）

伊蒂哈德的3岁小球童

已于 2024-04-04 12:53:03 修改

阅读量877

点赞数 8

分类专栏：深度学习文章标签：深度学习算法

于 2024-04-04 12:50:01 首次发布

本文链接：https://blog.csdn.net/CLP666666/article/details/137295709

版权

深度学习专栏收录该内容

5 篇文章 0 订阅

订阅专栏

1 全连接层误差反向传播

以简单的2层全连接层网络（即单隐藏层的多层感知机）为例分析误差反传算法。

1.1 网络模型

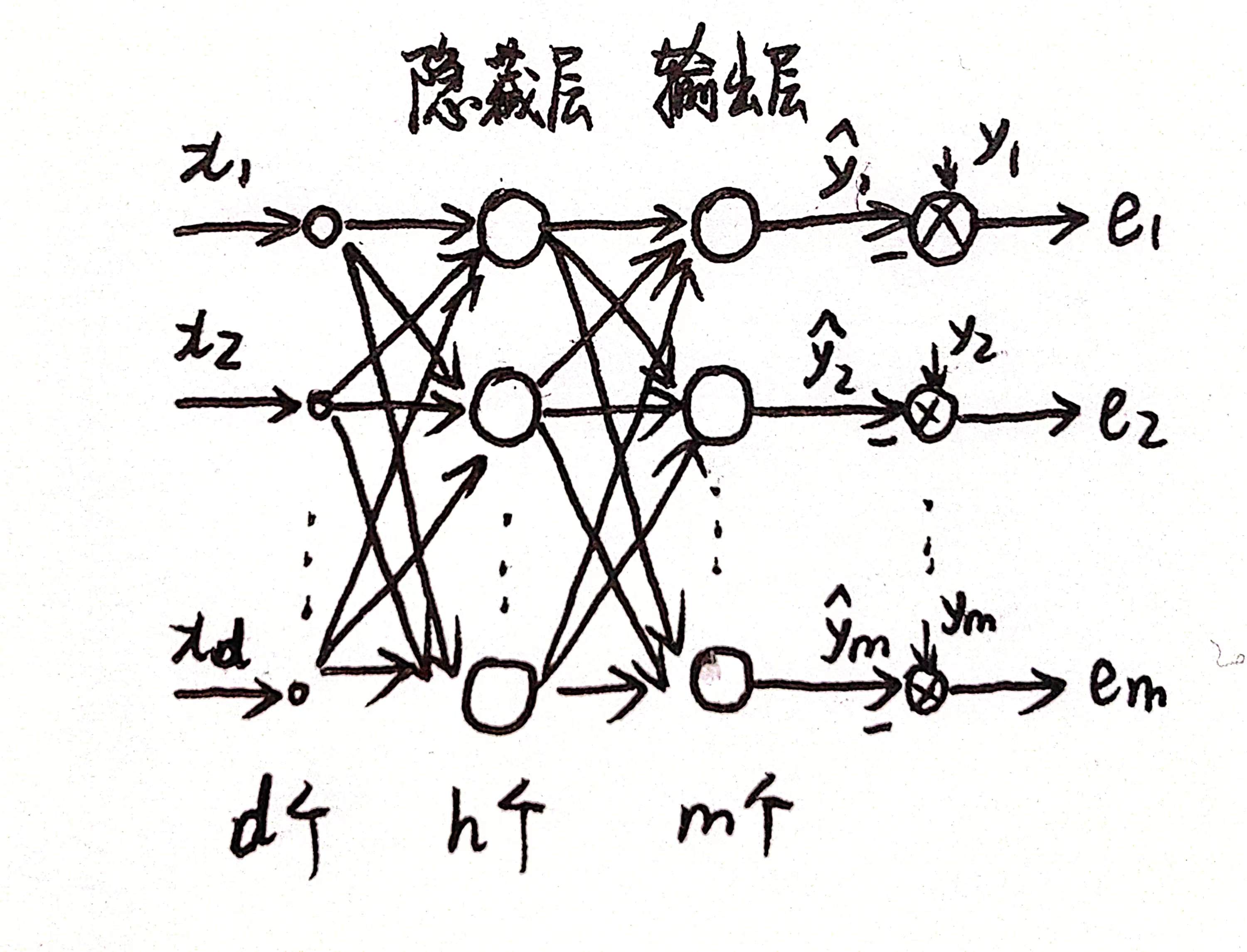
记号解释

上标表示层数，输入层为第0层，隐藏层为第1层。a表示神经元的输出，z表示神经元的线性输出，为了理解起见暂不采用向量表示。

$a^{[l]}_i$ 为 $l$ 层的第 $i$ 个神经元的输出， $z^{[l]}_i$ 为 $l$ 层的第 $i$ 个神经元的线性输出，满足

$z^{[l]}_i=\sum_jW^{[l]}_{i,j}a^{[l-1]}_j$

$a^{[l]}_i=\sigma(z^{[l]}_i)$

其中， $W^{[l]}_{i,j}$ 为第 $l$ 层第 $i$ 个神经元和前一层第 $j$ 个神经元的连接权值（包含了偏置项）， $\sigma(\cdot)$ 采为sigmoid函数，其导数为

${\sigma}'=\sigma(1-\sigma)$

1.2 前向传播

前向传播即输入经过隐藏层到输出层的传播。

$a^{[1]}_i=\sigma(z^{[1]}_i)=\sigma(\sum_jW^{[1]}_{i,j}x_j)$

$a^{[2]}_i=\sigma(z^{[2]}_i)=\sigma(\sum_jW^{[2]}_{i,j}a^{[1]}_j)$

${\hat y}_i =a^{[2]}_i$

$e_i=y_i-{\hat y}_i$

目标函数为

$J=\frac{1}{2}\sum_je_j^2$

1.3 误差反传

1.3.1 输出层权值更新

输出层神经元的权值只影响了该神经元的输出，因此以输出层第 $i$ 个神经元和前一层第 $j$ 个神经元的连接权值更新为例，有

$\frac{\partial J}{\partial w^{[2]}_{{i,j}}}=\frac{\partial J}{\partial e_i}\frac{\partial e_i}{\partial y_i}\frac{\partial y_i}{\partial a^{[2]}_i}\frac{\partial a^{[2]}_i}{\partial z^{[2]}_i}\frac{\partial z^{[2]}_i}{\partial w^{[2]}_{{i,j}}}=e_i\cdot(-1)\cdot1\cdot a^{[2]}_i(1-a^{[2]}_i)\cdot a^{[1]}_j$

令

$\delta^{[2]}_i=e_i\cdot a^{[2]}_i(1-a^{[2]}_i)=-\frac{\partial J}{\partial z^{[2]}_i}$

$\delta^{[2]}_i$ 里含有误差 $e_i$ ，因此可以认为误差 $e_i$ 反传给第2层（即输出层）的量就是 $\delta^{[2]}_i$ 。

则权值的更新公式为

$\Delta w^{[2]}_{{i,j}}=-\alpha\frac{\partial J}{\partial w^{[2]}_{{i,j}}}=\alpha \delta^{[2]}_i \cdot a^{[1]}_j$

由于单个神经元的Hebb规则是权值的调整量和输入输出的乘积成正比，对于权值 $w^{[2]}_{{i,j}}$ ，可以认为输入为 $\delta^{[2]}_i$ ，输出为 $a^{[1]}_j$ 。

1.3.2 隐藏层权值更新

对于隐藏层的权值来说，某个权值首先传到该隐藏层神经元的输出，然而该输出接下来会传到输出层的每个神经元的输出里，因此较为复杂，但本质也是多元函数求偏导数的链式求导法则：

$\frac{\partial J}{\partial w^{[1]}_{{i,j}}} =\frac{\partial J}{\partial z^{[1]}_i}\frac{\partial z^{[1]}_i}{\partial w^{[1]}_{{i,j}}}=\frac{\partial J}{\partial a^{[1]}_i}\frac{\partial a^{[1]}_i}{\partial z^{[1]}_i}\frac{\partial z^{[1]}_i}{\partial w^{[1]}_{{i,j}}} \\=(\frac{\partial J}{\partial e_1}\frac{\partial e_1}{\partial y_1}\frac{\partial y_1}{\partial a^{[2]}_1}\frac{\partial a^{[2]}_1}{\partial z^{[2]}_1}\frac{\partial z^{[2]}_1}{\partial a^{[1]}_i}+\frac{\partial J}{\partial e_2}\frac{\partial e_2}{\partial y_2}\frac{\partial y_2}{\partial a^{[2]}_2}\frac{\partial a^{[2]}_2}{\partial z^{[2]}_2}\frac{\partial z^{[2]}_2}{\partial a^{[1]}_i}+...+\frac{\partial J}{\partial e_m}\frac{\partial e_m}{\partial y_m}\frac{\partial y_m}{\partial a^{[2]}_m}\frac{\partial a^{[2]}_m}{\partial z^{[2]}_m}\frac{\partial z^{[2]}_m}{\partial a^{[1]}_i})\frac{\partial a^{[1]}_i}{\partial w^{[1]}_{{i,j}}}\\=\sum_{k=1}^m w^{[2]}_{{k,i}}e_k(-1)( a^{[2]}_k(1- a^{[2]}_k)) \cdot [(a^{[1]}_i(1-a^{[1]}_i))x_j]$

令

$\delta^{[1]}_i = \sum_{k=1}^m w^{[2]}_{{k,i}}e_k( a^{[2]}_k(1- a^{[2]}_k)) \cdot (a^{[1]}_i(1-a^{[1]}_i)) \\ = \sum_{k=1}^m w^{[2]}_{{k,i}}\delta^{[2]}_k{(a^{[1]}_i)}'=-\frac{\partial J}{\partial z^{[1]}_i}$

$\delta^{[1]}_i$ 里含有误差 $e$ ，因此可以认为误差 $e$ 反传到第1层（即隐藏层）的量就是 $\delta^{[1]}_i$ ，为了后续表达方便，下文中称 $\delta$ 为每一层的误差。

则权值的更新公式为

$\Delta w^{[1]}_{{i,j}}=-\alpha\frac{\partial J}{\partial w^{[1]}_{{i,j}}}=\alpha \delta^{[1]}_i \cdot x_j$

总结：

当前层误差为下一层误差的加权和再乘以当前层激活函数的导数。
当前层连接权值的更新调整量与当前层误差有关。

2 卷积神经网络误差反向传播

在卷积神经网络（CNN）中，同样有前向传播和反向传播，为将不同BP算法的思路进行整理，下面对CNN的BP算法进行简要介绍。对于CNN的详细介绍将在后续文章中给出。

2.1 池化层误差反向传播

卷积神经网络的基本结构是输入层-卷积层-池化层-全连接层，一般卷积层和池化层以组合的形式出现，可以有多个这样的组合。误差从输出进行反传时，首先传入全连接层，而全连接层的误差反传算法已在前面介绍过了，假定误差 $\delta$ 已经传到池化层，池化层没有参数学习，只需考虑误差的反向传播即可，即池化层前一层（一般是卷积层）的误差是多少。

基本思路是将卷积层和池化层（二维）转化为我们熟悉的神经网络结构形式，即将二维的层“压扁”成为单个神经元构成的层，两层之间的权重由池化方法决定，若是最大池化，则连接权值仅由0和1组成，若是平均池化，则连接权值是1/（池化窗口包含神经元的个数）。

然后利用全连接层所得出的结论得到卷积层的误差（加权和乘以激活函数的导数）。