KF、UKF、EKF、PF、FKF、DKF卡尔曼滤波KF、UKF、拓展卡尔曼滤波目标滤波研究（Matlab代码实现）

最新推荐文章于 2025-05-01 11:08:19 发布

吃兔子的大脑腐

最新推荐文章于 2025-05-01 11:08:19 发布

阅读量948

点赞数 34

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/CSDNQAQ/article/details/147588344

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

卡尔曼滤波（KF）及其变种在目标跟踪中的原理与应用

一、卡尔曼滤波（KF）基础原理与核心特性

二、扩展卡尔曼滤波（EKF）：非线性系统的局部线性化

三、无迹卡尔曼滤波（UKF）：无迹变换与高阶精度

四、粒子滤波（PF）：非高斯与非线性的蒙特卡洛方法

五、固定区间卡尔曼滤波（FKF）：离线数据平滑

六、分布式卡尔曼滤波（DKF）：多传感器协同估计

七、典型应用场景对比

八、目标滤波领域研究热点

九、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

卡尔曼滤波（KF）及其变种在目标跟踪中的原理与应用

一、卡尔曼滤波（KF）基础原理与核心特性

基本原理
卡尔曼滤波（KF）是一种基于贝叶斯估计的递归算法，通过融合预测值和测量值实现对动态系统状态的最优估计。其核心步骤分为预测与更新：
核心假设
- 系统为线性动态模型，且噪声服从高斯分布。
- 状态转移矩阵（ΦΦ）和观测矩阵（HH）均为线性。
优势与局限
- 优势：计算高效、实时性强，适用于线性高斯系统。
- 局限：无法直接处理非线性或非高斯问题。

二、扩展卡尔曼滤波（EKF）：非线性系统的局部线性化

改进机制
EKF通过一阶泰勒展开对非线性函数进行局部线性化，利用雅可比矩阵（A=∂f∂xA=∂x∂f和H=∂h∂xH=∂x∂h）近似非线性模型，从而应用标准KF框架。
典型应用
- 电力系统状态估计：EKF用于动态状态估计，但在强非线性系统中存在截断误差，需结合自适应方法提升鲁棒性。
- 机器人导航：处理传感器非线性观测方程（如雷达测距）。
局限性
- 一阶线性化引入近似误差，可能导致滤波发散。
- 雅可比矩阵计算复杂，对初值敏感。

三、无迹卡尔曼滤波（UKF）：无迹变换与高阶精度

核心思想
UKF通过 无迹变换（UT） 选择Sigma点（通常为2n+12n+1个，nn为状态维度），直接对非线性变换后的均值和协方差进行采样，避免雅可比矩阵计算，达到三阶泰勒精度。
流程步骤
- Sigma点生成：基于当前状态均值和协方差矩阵的Cholesky分解。
- 非线性传播：将Sigma点代入非线性函数，计算变换后的均值和协方差。
- 卡尔曼增益更新：类似KF框架，但基于Sigma点的统计特性。
优势对比EKF
- 精度更高：UKF在均值和协方差估计中保留高阶项，尤其适用于强非线性系统（如自动驾驶定位）。
- 实现简单：无需计算导数，适合复杂非线性模型。

四、粒子滤波（PF）：非高斯与非线性的蒙特卡洛方法

基本原理
PF通过重要性采样生成粒子集近似后验概率密度，每个粒子代表状态空间中的一个假设，权重反映其似然概率。通过重采样避免粒子退化。
核心步骤
- 预测：根据过程模型生成新粒子。
- 权重更新：基于观测似然调整粒子权重。
- 重采样：按权重分布重新抽取粒子，保持多样性。
应用场景
- 多目标跟踪：处理多模态分布（如目标遮挡、交叉轨迹）。
- 复杂环境：如视觉SLAM中结合RGB-D传感器处理非高斯噪声。
局限性
- 计算复杂度高：粒子数随状态维度指数增长。
- 重采样导致样本贫化，需结合优化策略（如自适应粒子数）。

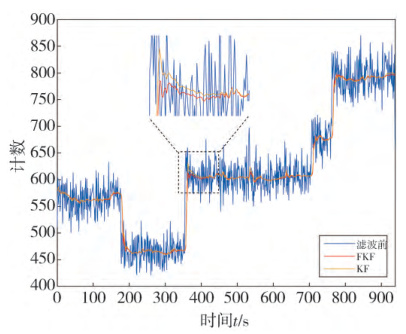
五、固定区间卡尔曼滤波（FKF）：离线数据平滑

原理与特点
FKF属于平滑算法，利用全部观测数据（固定时间区间）进行后向修正，典型代表为Rauch-Tung-Striebel（RTS）平滑器。其通过前向KF和后向递归方程提升估计精度。
应用场景
- 飞行试验数据处理：离线优化导航轨迹，减少实时滤波的累积误差。
- 地震信号处理：结合自适应滤波消除非平稳噪声。
优势
- 精度优于在线KF，适合事后分析。
- 通过协方差反向传播修正历史估计。

六、分布式卡尔曼滤波（DKF）：多传感器协同估计

协同机制
DKF通过共识算法实现多传感器信息融合，每个节点仅需局部观测，通过通信网络达成全局一致估计。典型方法包括微卡尔曼滤波（Micro-KF）与共识滤波器结合。
数学模型
- 局部预测：各节点独立运行KF，生成局部估计。
- 全局共识：通过加权平均或ADMM优化实现状态和协方差矩阵的一致性。
应用场景
- 大规模传感器网络：如环境监测、智能电网状态估计。
- 无人机编队：协同定位与避障。

七、典型应用场景对比

滤波器	适用系统特性	计算复杂度	典型场景
KF	线性、高斯	低	惯性导航、金融时序预测
EKF	弱非线性、高斯	中	机器人SLAM、电力系统
UKF	强非线性、高斯	中高	自动驾驶、航天器轨道
PF	非线性、非高斯	高	多目标跟踪、视觉定位
FKF	离线、线性/非线性	高	飞行试验后处理、地震
DKF	多传感器、分布式	中高	智能电网、无人机集群

八、目标滤波领域研究热点

非线性滤波优化
- UKF与深度学习的结合：利用神经网络建模非线性函数，提升UKF的自适应性。
- 自适应PF：动态调整粒子数和重采样策略，平衡精度与效率。
多传感器融合
- 异构传感器融合：结合LiDAR、相机和IMU数据，通过DKF实现鲁棒定位。
- 边缘计算优化：降低DKF通信开销，适用于资源受限的物联网节点。
实时性与鲁棒性提升
- 强跟踪滤波（STF） ：引入渐消因子抑制模型失配，应用于EKF提升鲁棒性。
- 相关滤波（CF） ：在视觉跟踪中结合核相关滤波（KCF），实现高速目标检测。

九、结论

卡尔曼滤波及其变种在目标跟踪中各有侧重：KF和EKF适用于线性或弱非线性场景，UKF在强非线性系统中表现更优，PF处理非高斯问题灵活但计算量大，FKF和DKF分别服务于离线和分布式需求。未来研究将聚焦于算法融合（如UKF+PF）、计算效率优化（如GPU加速PF）以及新型传感器融合架构，以应对复杂动态环境下的实时跟踪挑战。

📚2 运行结果

部分代码：

%% 基本离散kalman滤波
Xkf=kalman(Xkf,u_1,Z,H,P0,Q,R,phi,Tau,N);

%% 限制K减小的kalman滤波
Xkf_rk=kalman_restrain_K(Xkf_rk,u_1,Z,H,P0,Q,R,phi,Tau,N);

%% 带遗忘因子的kalman滤波
Xkf_ff=kalman_forgetting_factor(Xkf_ff,u_1,Z,H,P0,Q,R,phi,Tau,N);

%% 扩大P的kalman滤波
Xkf_Sk=kalman_Sk(Xkf_Sk,u_1,Z,H,P0,Q,R,phi,Tau,N);

%误差分析
for i=1:N

Err_Observation(i)=RMS(X(:,i),Z(:,i));%滤波前的误差
Err_KalmanFilter(i)=RMS(X(:,i),Xkf(:,i));%滤波后的误差
Err_rkKalmanFilter(i)=RMS(X(:,i),Xkf_rk(:,i));%滤波后的误差
Err_ffKalmanFilter(i)=RMS(X(:,i),Xkf_ff(:,i));%滤波后的误差
Err_adKalmanFilter(i)=RMS(X(:,i),Xkf_Sk(:,i));%滤波后的误差
end
mean_Observation=mean(Err_Observation);
mean_KalmanFilter=mean(Err_KalmanFilter);
mean_fixKalmanFilter=mean(Err_rkKalmanFilter);
mean_ffKalmanFilter=mean(Err_ffKalmanFilter);
mean_adKalmanFilter=mean(Err_adKalmanFilter);

%% 画图
figure
hold on;box on;
t=(0:1:N-1);
plot(t,S(1,:),'-','LineWidth',1);%理论轨迹
plot(t,X(1,:),'--','LineWidth',1);%实际轨迹
plot(t,Z(1,:),'-o','LineWidth',1);%观测轨迹
plot(t,Xkf(1,:),':','LineWidth',2);%卡尔曼滤波轨迹
plot(t,Xkf_rk(1,:),'-.','LineWidth',2);%卡尔曼滤波轨迹
plot(t,Xkf_ff(1,:),'-x','LineWidth',2);%卡尔曼滤波轨迹
plot(t,Xkf_Sk(1,:),'--s','LineWidth',2);%卡尔曼滤波轨迹
% M=M';
% plot(M(1,:),'k','LineWidth',1);%一步预测轨迹
legend('理论轨迹','实际运动轨迹','观测轨迹','基本滤波后轨迹','限制k减小滤波后轨迹','带遗忘因子卡尔曼滤波','扩大P的卡尔曼滤波');
xlabel('横坐标 T/s');
ylabel('纵坐标 X/m');

figure
hold on;box on;
plot(t,Err_Observation,'-');
plot(t,Err_KalmanFilter,'--');
plot(t,Err_rkKalmanFilter,'-.');
plot(t,Err_ffKalmanFilter,'-x');
plot(t,Err_adKalmanFilter,'-s');
% legend('滤波前误差',num2str(mean_Observation),'基本滤波后误差','固定增益滤波后误差');
legend(sprintf('滤波前误差%.03f',mean_Observation),sprintf('基本滤波后误差%.03f',mean_KalmanFilter),...
sprintf('限制k减小增益滤波后误差%.03f',mean_fixKalmanFilter),sprintf('带遗忘因子滤波后误差%.03f',mean_ffKalmanFilter),...
sprintf('扩大P的滤波后误差%.03f',mean_adKalmanFilter));
xlabel('观测时间/s');
ylabel('误差值');