Franka机器人Mujoco多种控制器仿真运动

最新推荐文章于 2025-05-12 22:19:18 发布

CapRogers1

最新推荐文章于 2025-05-12 22:19:18 发布

阅读量969

点赞数 22

文章标签：机器人控制算法 Mujoco

本文链接：https://blog.csdn.net/CapRogers1/article/details/147114342

版权

Franka机器人是由德国公司Franka Emika 研发的一款协作型机器人，主打高精度、灵活性和人机协作能力。其核心特点为：

灵敏力控：配备高精度扭矩传感器，每个关节可实时感知外力，实现安全的人机协作（符合ISO/TS 15066标准）。
模块化设计：7自由度机械臂（仿人手臂结构），重复定位精度可达±0.1mm，适合精密操作。
易编程：
- 支持拖拽示教（直接手动引导机器人记录动作）。
- 提供开源框架（如LibFranka、ROS驱动），方便开发者自定义控制。
集成化：内置摄像头、触觉传感器，部分型号支持模块化末端执行器（如夹爪、吸盘等）。
移动性：轻量化设计（约18kg），可快速部署在不同工作场景。

以该机器人为例进行控制仿真

准备部分

Solidworks导出urdf

首先在solidworks当中打开该模型并设置其初始姿态如下图所示

利用Modified Denavit–Hartenberg也即修正DH法建立其DH坐标系建立该机器人的末端姿态和关节转角的关系。MDH表格如下

Franka机器人MDH
θ/rad	d/mm	a/mm	α/rad
θ1	333	0	0
θ2	0	0	-pi/2
θ3	316	0	pi/2
θ4	0	82.5	pi/2
θ5	384	-82.5	-pi/2
θ6	0	0	pi/2
θ7	107	88	pi/2

接下来将设置好的模型转化为urdf，具体可以参考机器人Rviz+matlab仿真详细步骤，从solidworks到urdf以及机器人编程控制，以ER50-C20为例_matlab urdf-CSDN博客

matlab验证MDH

我们可以将上述MDH参数放到matlab当中用机器人工具箱验证，安装机器人工具箱同样可以参考上述网址。在导入工具箱后创建一个名字叫做franka_teach.m的文件并设置下列内容：

clear;clc;

l0=Link([0        0.333        0              0                0],'modified');
l1=Link([0        0            0              -pi/2            0],'modified');
l2=Link([0        0.316        0              pi/2             0],'modified');
l3=Link([0        0            0.0825         pi/2             0],'modified');
l4=Link([0        0.3840       -0.0825        -pi/2            0],'modified');
l5=Link([0        0            0              pi/2             0],'modified');
l6=Link([0        0.107        0.088          pi/2             0],'modified');
% l7=Link([0        0            0.088          pi/2             0],'standard');
robot=SerialLink([l0 , l1 , l2 , l3 , l4 , l5, l6],'name','Franka');

q=[0 pi/6 -pi/3 -pi/3 pi/3 pi/12,pi];
% q=[-2.96011212  2.60746262  0.92656756 -1.44677419  1.66116245  2.98399905];
T1=robot.fkine(q);disp(T1);Rm = [T1.n,T1.o,T1.a];
Q=robot.ikine(T1);
fprintf('\nq=\n\n');ispie(Q)
eul = rotm2eul(Rm, 'xyz');
roll = eul(1);pitch = eul(2);yaw = eul(3);
xd = [T1.t',roll,pitch,yaw];disp(xd)
view(3)
robot.teach([0 0 0 0 0 0 0])

代码解释如下：

clear; clc;代表清除工作区和命令面板的所有数据防止程序数据影响；
L#代表定义一个包含多个关节链接的数组，其中每个关节用一个 Link 对象表示；
robot=SerialLink代表创建一个串联机器人模型 Franka，使用 l# 中定义的关节链接；
从定义q到disp这一挣断代码用于验证一组解的返回情况，先将q姿态的正解得到一个齐次矩阵，再将其反解验证；
打开一个交互式窗口，用于控制和可视化机器人并设置表示各个关节的初始角度为零。

将得到Franka机器人的结构简图，可以自由操控检测是否和实际的franka运动方式一致：

安装mujoco200

MuJoCo（Multi-Joint Dynamics with Contact）是一款专注于高精度物理仿真的开源引擎，广泛用于机器人控制、强化学习和生物力学研究。在Ubuntu系统下，它提供高效的动力学计算（如复杂碰撞和摩擦建模），支持Python（通过mujoco-py）和C接口，并内置3D可视化工具（simulate）。其优势在于逼真的接触力学和计算效率，常用于训练强化学习智能体（如OpenAI Gym环境）或验证机器人算法，但需手动编写XML模型文件，相比其他仿真工具（如PyBullet）更底层。自2021年免费开源后，成为科研和工业仿真的重要工具。

首先在ubuntu的~/目录下打开终端创建mujoco的文件夹

mkdir ~/.mujoco
cd ~/.mujoco

下载mujoco，我们可以访问网址MuJoCo选择对应的mujoco版本，如果是win系统则选择win32或者win64，如果是linux版本则直接选择linux

以linux框架为例，利用wget工具直接下载mujoco200

sudo apt-get install wget -y
wget https://www.roboti.us/download/mujoco200_linux.zip

所下载的mujoco压缩包是便携式文件直接解压即可使用：

unzip mujoco200_linux.zip
mv mujoco200_linux mujoco200
rm mujoco200_linux.zip

虽然mujoco已经开源，但仍旧需要密钥，密钥文件已经开源，我们可以在bin目录下创建密钥文件

cd ~/.mujoco/mujoco200/bin
touch mjkey.txt
sudo apt-get install gedit -y
gedit mjkey.txt

在打开的文件夹内部输入下列内容：

MuJoCo Pro Individual license activation key, number 7777, type 6.

Issued to Everyone.

Expires October 18, 2031.

Do not modify this file. Its entire content, including the
plain text section, is used by the activation manager.

9aaedeefb37011a8a52361c736643665c7f60e796ff8ff70bb3f7a1d78e9a605
0453a3c853e4aa416e712d7e80cf799c6314ee5480ec6bd0f1ab51d1bb3c768f
8c06e7e572f411ecb25c3d6ef82cc20b00f672db88e6001b3dfdd3ab79e6c480
185d681811cfdaff640fb63295e391b05374edba90dd54cc1e162a9d99b82a8b
ea3e87f2c67d08006c53daac2e563269cdb286838b168a2071c48c29fedfbea2
5effe96fe3cb05e85fb8af2d3851f385618ef8cdac42876831f095e052bd18c9
5dce57ff9c83670aad77e5a1f41444bec45e30e4e827f7bf9799b29f2c934e23
dcf6d3c3ee9c8dd2ed057317100cd21b4abbbf652d02bf72c3d322e0c55dcc24

如图所示确信内容如下：

将该路径添加到环境当中：

export LD_LIBRARY_PATH=~/.mujoco/mujoco200/bin/

运行一个人体模型的mojoco仿真：

cd ~/.mujoco/mujoco200/bin
./simulate ../model/humanoid.xml

得到mujoco的仿真界面：

可以前往~/.mujoco/mujoco200/model目录查看mujoco自带的下列仿真模型描述文件：

urdf转为xml

首先定位到solidworks导出的urdf文件，以UR10为例：

我们只需要在机器人描述文件的名字后添加mujoco部分的内容让它能够被mujoco编译：

  <mujoco>
    <compiler 
    meshdir="/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/meshes/" 
    balanceinertia="true" 
    discardvisual="false" />
  </mujoco>

例如我将Franka机器人的SW导出的文件放置到了/home/xw9527/.mujoco/mujoco200/model/下：

将模型文件定义到你导出的urdf文件的meshes文件夹

meshdir="/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/meshes/"

然后到mujoco的文件夹当中将该urdf编译为xml文件：

./compile /home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.urdf /home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml

编译的位置如上述代码所示放置到/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml当中

接下来可以在bin文件夹运行此xml文件

cd ~/.mujoco/mujoco200/bin
./simulate ../model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml

得到如下仿真结果：

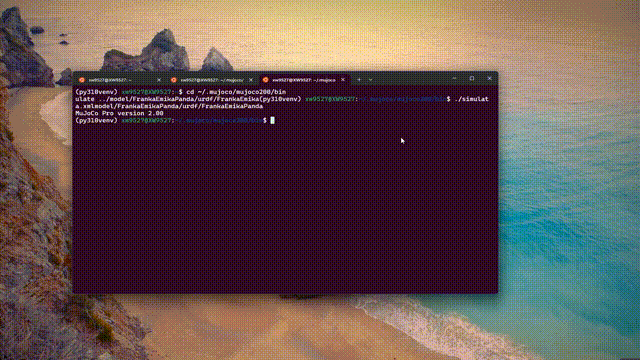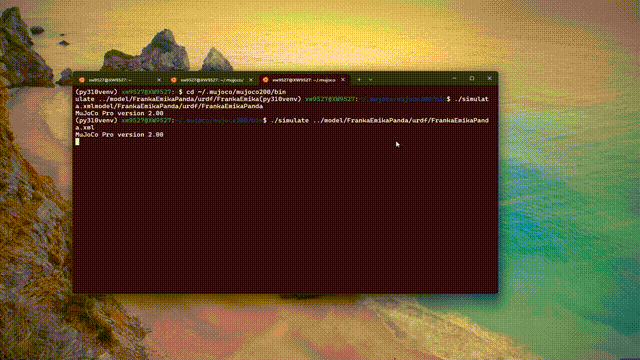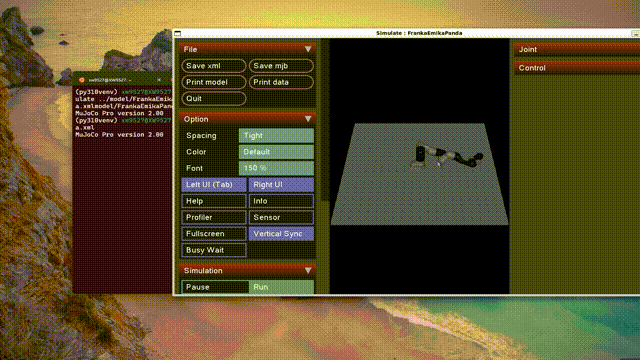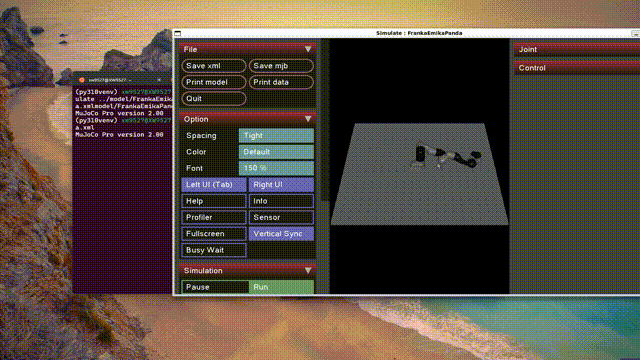
我们可以发现当下的机械臂是不能控制的，因为缺少控制器，机械臂只会从初始位置受到重力作用直接摔落，因此可以添加mujoco控制器

同样需要打开机器人的描述文件，对应到mujoco是对应的xml文件，需要在该文件</worldbody>后添加控制器

mujoco当中控制器分为以下几种：

力矩控制器，对关节施加力或者力矩控制关节运动，结合大多数电机力矩环控制，非常贴切市场应用。同时还可以结合机器人动力学提高控制精度；
速度控制器，速度环控制一般运用在小车或者轮足等移动机器人上进行匀速控制，本案例非常不适合用速度控制；
位置控制器，结合伺服驱动电机控制电机到指定角度，也较为方便，但是控制精度取决于电机内部电流环控制，仿真使用位置控制会极大简化算法，类似于rviz的joint控制，此案例也比较合适使用位置控制；
模型预测控制，采用强化学习或者基于优化或学习算法实时生成控制信号，控制效果较好同时适用性高，例如MPC算法。

力矩控制模式

本案例采用不添加动力学前馈的力矩控制，采用以下几种力矩控制器仿真控制：我们在xml文件当中添加如下控制器描述内容：

    <actuator>
        <motor name="a1" joint="j1" ctrllimited="true" ctrlrange="-87 87" />
        <motor name="a2" joint="j2" ctrllimited="true" ctrlrange="-87 87" />
        <motor name="a3" joint="j3" ctrllimited="true" ctrlrange="-87 87" />
        <motor name="a4" joint="j4" ctrllimited="true" ctrlrange="-87 87" />
        <motor name="a5" joint="j5" ctrllimited="true" ctrlrange="-12 12" />
        <motor name="a6" joint="j6" ctrllimited="true" ctrlrange="-12 12" />
        <motor name="a7" joint="j7" ctrllimited="true" ctrlrange="-12 12" />
</actuator>

最后得到的xml文件如下：

franka是冗余串联机器人，总共7个理论自由度，因此需要添加7个力矩控制并设置控制范围ctrlrange="-87 87"，如果不添加控制范围只需要改为ctrllimited="False"并去除后面的控制范围即可

PD控制

静态PD控制

不考虑在时间作用下产生的累积误差我们可以使用PD控制，让它能够位置和速度都快速响应抵达指定位置：

首先我们定义机械臂要抵达一个位置 $p_{desire}$ ，但是其实际位置为 $p_{actual}$ ，两者之间的误差为：

$e = p_{desire} - p_{actual}$

这个误差可以表示当前位置的待变化量，同样的，通过传感器采集或者离散微分的方式我们可以得到：

$\dot{e} = \dot{p}_{desire} - \dot{p}_{actual}$

也可以理解为速度误差等于期望速度和实际速度的差值

将两者结合就得到了力矩计算式，其中的Kp和Kd则是对应的参数，反映位置和速度对于当前误差的响应程度，一般设置到一个合适的数值效果才是最好的，太小基本无响应，太大响应过快导致超调：

$\tau _{_{PD}} = K_{p}e + K_{d}\dot{e}$

基于上述理论我们编写对应的控制部分代码：

        # 获取当前关节角度和速度
        current_qpos = data.qpos[:7]  # 取前7个值
        current_qvel = data.qvel[:7]
        
        # 计算误差 e = 目标角度 - 当前角度
        error = desired_qpos - current_qpos
        d_error = -current_qvel  # 角速度误差：目标速度为0，所以 d_error = -current_qvel

        # 计算 PD 力矩
        torque = Kp * error + Kd * d_error
        data.ctrl[:7] = torque  # 发送力矩控制信号

然后设置每一个关节的PD控制参数：

Kp = np.array([500, 300, 50, 300, 50, 300, 20])  # 比例增益
Kd = np.array([20, 10, 2, 10, 2, 8, 1])  # 微分增益

设置默认参数如上，一般参数无法直接复制到一个机械臂上直接就适用，需要多次调整才能适用，上述则是适合Franka仿真的参数，一般建议初始设置不要过大。

然后设置一个机器人轨迹，让机械臂按照此轨迹在一个控制周期下不停控制到期望位置实现一段连续轨迹的运动，为实验控制参数，我们设置期望轨迹为零位：

desired_qpos = np.zeros(7)  # 目标关节角度 (7个关节)

列出总代码：

import mujoco
import mujoco.viewer
import numpy as np
import time

model = mujoco.MjModel.from_xml_path("/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml")  
data = mujoco.MjData(model)

Kp = np.array([500, 300, 50, 300, 50, 300, 20]) 
Kd = np.array([20, 10, 2, 10, 2, 8, 1])  
desired_qpos = np.zeros(7)  

with mujoco.viewer.launch_passive(model, data) as viewer:
    last_qvel = np.zeros(7)  
    while viewer.is_running():
        start = time.time()
        
        current_qpos = data.qpos[:7]  
        current_qvel = data.qvel[:7]
        
        error = desired_qpos - current_qpos
        d_error = -current_qvel  

        torque = Kp * error + Kd * d_error
        data.ctrl[:7] = torque  # 发送力矩控制信号

        mujoco.mj_step(model, data)

        viewer.sync()

        # 200Hz
        time.sleep(max(0, 0.005 - (time.time() - start)))

将此控制程序放置在~/.mujoco/mujoco200/model/FrankaEmikaPanda/Franka_Ctrl/mujoco当中运行python程序即可

不过此前需要安装python的mujoco通讯模块：

pip install mujoco

例如下所示，由于此处已经安装，显示如下：

安装完成mujoco后运行此代码：

python zero_pd_pos.py

得到如下结果：

发现机械臂不会像之前那样无力直接摔下了，而且通过观察发现刚开始位置和力矩基本会有变化但是很快就达到稳态，臂体也就刚开始有轻微晃动，说明了控制器很好的把机器人控制在原位了。

我们可以和其他参数比较一下，例如将参数设置为原来的0.05：

Kp = np.array([500, 300, 50, 300, 50, 300, 20])*0.05
Kd = np.array([20, 10, 2, 10, 2, 8, 1])*0.05  # 微分增益

很显然参数对于机械臂控制精度有较大影响。

动态PD控制

测试了参数可行后再考虑动态控制，先不考虑机械臂的逆运动学。

我们可以实现从姿态A到姿态B的平滑过渡，例如：

# 目标关节角度
desired_qpos_final = np.array([0, pi/4, 0, -pi/2, 0, 3*pi/4, 0])  # 目标关节角度
initial_qpos = np.zeros(7)  # 初始关节角度全零
transition_time = 6  # 过渡时间6秒

while running:
    t = min(elapsed_time - 6, transition_time)  # 在过渡时间内逐渐变化
    desired_qpos = initial_qpos + (desired_qpos_final - initial_qpos) * (t / transition_time)

同样，我们给机器人每一个关节都施加对应的控制信号，例如给每一个关节都施加一个正弦信号看看PD控制的动态控制能力：

设置正弦函数振幅和周期：

desired_amplitude = np.pi / 8  # 振幅 ±π/8

# 目标角度：用正弦波描述
frequency = 1  # 频率，1 Hz 即每秒一个完整周期

将期望姿态设置为正弦波函数：

        start = time.time()

        
        # 计算目标角度：正弦波形式
        t = time.time()  # 当前时间
        desired_qpos = desired_amplitude * np.sin(2 * np.pi * frequency * t) * np.ones(7)  # 每个关节都做相同的振荡

以正弦函数为例：在此期望姿态下同样将PD控制力矩输出给Mujoco：

import mujoco
import mujoco.viewer
import numpy as np
import time

model = mujoco.MjModel.from_xml_path("/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml") 
data = mujoco.MjData(model)

Kp = np.array([500, 300, 50, 300, 50, 300, 20])  
Kd = np.array([20, 10, 2, 10, 2, 8, 1])  
desired_amplitude = np.pi / 8  

frequency = 1 

with mujoco.viewer.launch_passive(model, data) as viewer:
    last_qvel = np.zeros(7)  
    while viewer.is_running():
        start = time.time()

        current_qpos = data.qpos[:7]  
        current_qvel = data.qvel[:7]
        
        t = time.time() 
        desired_qpos = desired_amplitude * np.sin(2 * np.pi * frequency * t) * np.ones(7)  
        

        error = desired_qpos - current_qpos
        d_error = -current_qvel 

        torque = Kp * error + Kd * d_error
        data.ctrl[:7] = torque  

        mujoco.mj_step(model, data)

        viewer.sync()

        # 200Hz 控制频率
        time.sleep(max(0, 0.005 - (time.time() - start)))

得到结果如下：

施加逆运动学

此处可以参考机器人Rviz+matlab仿真详细步骤，从solidworks到urdf以及机器人编程控制，以ER50-C20为例-CSDN博客

当中的机器人逆运动学函数部分，唯一区别的在于机械臂自身的MDH参数不一致，机器人工具箱同样适用冗余机器人的逆运动学求解，不过本人测试发现当机器人驱动自由度高于10后工具箱不再好用。此处使用工具箱并给出代码：

import numpy as np
from roboticstoolbox import DHRobot, RevoluteMDH
from spatialmath import SE3

pi = np.pi


def ik_Franka(target_pose):
    l0 = RevoluteMDH(d=333, a=     0, alpha=0    )
    l1 = RevoluteMDH(d=0  , a=     0, alpha=-pi/2)
    l2 = RevoluteMDH(d=316, a=     0, alpha= pi/2)
    l3 = RevoluteMDH(d=0  , a=  82.5, alpha= pi/2)
    l4 = RevoluteMDH(d=384, a= -82.5, alpha=-pi/2)
    l5 = RevoluteMDH(d=0  , a=     0, alpha= pi/2)
    l6 = RevoluteMDH(d=107, a=    88, alpha= pi/2)

    robot = DHRobot([l0, l1, l2, l3, l4, l5, l6], name='Franka')

    while True:
        xyz = target_pose[:3]  
        rpy = target_pose[3:]  
        T = SE3(xyz) * SE3.RPY(rpy, order='zyx')

        result = robot.ikine_LM(T)

        q = result.q  
        success = result.success  
        err = result.residual  

        if((-np.pi/2 <= q[1] <= np.pi/2) and (-2.9 <= q[3] <= 0.3) and (0 <= q[5] <= np.pi)):
            break
        else:
            print("Joint angle q[1] out of bounds, recalculating...")
            
    print("Joint Angles:", q)
    print("Success:", success)
    print("Error:", err)
    # robot.plot(q)

    return q, err


def compute_smooth_ik(target_pose, last_q):
    robot = DHRobot([
        RevoluteMDH(d=333, a=     0, alpha=0    ),
        RevoluteMDH(d=0  , a=     0, alpha=-pi/2),
        RevoluteMDH(d=316, a=     0, alpha= pi/2),
        RevoluteMDH(d=0  , a=  82.5, alpha= pi/2),
        RevoluteMDH(d=384, a= -82.5, alpha=-pi/2),
        RevoluteMDH(d=0  , a=     0, alpha= pi/2),
        RevoluteMDH(d=107, a=    88, alpha= pi/2)
    ], name='Franka')

    xyz = target_pose[:3]  
    rpy = target_pose[3:]  
    T = SE3(xyz) * SE3.RPY(rpy, order='zyx')
    result = robot.ikine_LM(T, q0=last_q)  

    if result.success:
        delta_q = np.sum((result.q - last_q)**2)
        if delta_q < 1:
            return result.q  
        else:
            print("Transition not smooth, delta_q:", delta_q)
    else:
        print("IK failed for pose:", target_pose)

    return last_q

同样设置了两个逆运动学函数，均采用工具箱，ik_Franka主要基于静态和单姿态求解，而compute_smooth_ik函数用于求解连续姿态，动态求解，具体依旧可以参考机器人Rviz+matlab仿真详细步骤，从solidworks到urdf以及机器人编程控制，以ER50-C20为例-CSDN博客

本处不再赘述，将上述代码命名为ik_fr.py

编写上述逆运动学函数后我们只需要调用此逆解函数直接通过给轨迹来控制机器人

import ik_fr
import numpy as np

static_trace = [-449.5000,109.5000,257.3000,-pi/2,0,0] #示例的静态轨迹XYZRPY
q = ik_fr.ik_Franka(static_trace)

将此得到的q以特定的频率递交给mujoco控制代码的desired_qpos当中即可实现静态或者动态的逆运动学结合PD控制。

滑模控制

我们已经知道PD控制让机器人位置和速度都快速收敛，减少振动响应快速抵达期望姿态，但是PD控制在部分环境下依旧存在控制精度不高，而且当轨迹不固定的情况下控制会良莠不齐，部分轨迹控制效果好，部分很差，为提高机器人控制器，提出鲁棒性更加好的滑模控制方法：

首先引用之前的误差：

$e = p_{desire} - p_{actual}$

$\dot{e} = \dot{p}_{desire} - \dot{p}_{actual}$

我们都知道 $e$ 和 $\dot{e}$ 分别代表位置和速度的误差表示变量，对于Franka，其为1*7的向量，同样让两者快速收敛，将两者组合为一个函数S

$s = e + \lambda\dot{e}$

设计的目标就是让这个滑模面S收敛到0（理想情况下），那么如何让S收敛到0，我们可以设计一个滑模控制律，最简单的就是使用切换函数：

$u = \alpha *s*sgn(s) + \beta * s$

这样就和两个斜坡组成的面一样让小球停在目标位置，当其跳过一个面用切换函数sgn重新收敛到目标位置，列出下列代码：

首先设置参数：

lambda_param = np.array([ 0.1, 0.1,  0.1, 0.1,  0.1, 0.11, 0.12])  # 滑模增益
alpha_param =  np.array([  36,   8,    1,   1,    1, 0.38, 0.01])  # 符号项增益
beta_param =   np.array([3600, 800,   20,  80,   10,    8,    1])  # 控制增益

基于上述式：

        current_qpos = data.qpos[:7]  
        current_qvel = data.qvel[:7]
        
        # 计算误差 e = 目标角度 - 当前角度
        error = desired_qpos - current_qpos
        d_error = -current_qvel  # 角速度误差

        # 计算滑模面
        s = error + lambda_param * d_error

        # 滑模控制律
        control_signal = alpha_param * s * np.sign(s) + beta_param * s

同样结合mujoco编写代码：

import mujoco
import mujoco.viewer
import numpy as np
import time

model = mujoco.MjModel.from_xml_path("/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml") 
data = mujoco.MjData(model)

pi = 3.1415926

lambda_param = np.array([ 0.1, 0.1,  0.1, 0.1,  0.1, 0.11, 0.12]) 
alpha_param =  np.array([  36,   8,    1,   1,    1, 0.38, 0.01]) 
beta_param =   np.array([3600, 800,   20,  80,   10,    8,    1]) 

desired_qpos_start = np.array([0, 0, 0, 0, 0, 0, 0])  

desired_qpos_end = np.array([0, pi/4, 0, -pi/2, 0, 3*pi/4, 0])  

with mujoco.viewer.launch_passive(model, data) as viewer:
    last_qvel = np.zeros(7)  
    start_time = time.time()  

    while viewer.is_running():
        current_time = time.time() - start_time
        
        if current_time < 6:
            desired_qpos = desired_qpos_start
        else:
            transition_time = min(current_time - 6, 6)  
            alpha = transition_time / 6  
            desired_qpos = (1 - alpha) * desired_qpos_start + alpha * desired_qpos_end

        current_qpos = data.qpos[:7]  
        current_qvel = data.qvel[:7]
        
        error = desired_qpos - current_qpos
        d_error = -current_qvel  

        s = error + lambda_param * d_error

        control_signal = alpha_param * s * np.sign(s) + beta_param * s
        data.ctrl[:7] = control_signal 

        mujoco.mj_step(model, data)

        viewer.sync()

        # 200Hz
        time.sleep(max(0, 0.005 - (time.time() - current_time)))

将其命名为linar_smc_mov.py并运行：

python linar_smc_mov.py

我们可以通过mujoco接口输出每一时刻的关节数据和期望作差，同样的PD控制的数据也同样可以作差比较两控制器的控制精度，不过这是控制算法人员等所需，此处不再给出，不过我们可以明显知道滑模控制相比PD有更强的适应性和鲁棒性。

可调增益PD控制

PD控制在部分环境下依旧存在控制精度不高，而且当轨迹不固定的情况下控制会良莠不齐，那么基于此，可以设置一种参数随着控制情况实时改变，再提高控制精度的方法。

已知：

$\tau _{_{PD}} = K_{p}e + K_{d}\dot{e}$

那么可调增益PD控制的输出力矩则为：

$\tau _{_{PDadj}} = K_{padj}e + K_{dadj}\dot{e}$

其中的 $K_{padj}$ 和 $K_{dadj}$ 都是随时变化的量，主要和 $e$ 以及 $\dot{e}$ 这两个量相关：

$K_{padj} = K_{p0} + \lambda e$

$K_{dadj} = K_{d0} + \lambda\dot{e}$

其中Kp0和Kd0是设置的初始参数值：

首先列出参数：

Kp0 = np.array([1000, 800, 500, 300, 50, 80, 2.5])  # 初始比例增益
Kd0 = np.array([20, 10, 10, 10, 0.5, 0.5, 0.1])  # 初始微分增益
lambda_param = np.array([0.1, 0.1, 0.1, 0.05, 0.001, 0.01, 0.0005])  # 每个关节的自适应权重

给出控制核心：

        # 计算误差 e = 目标角度 - 当前角度
        error = desired_qpos - current_qpos
        d_error = -current_qvel  # 角速度误差：目标速度为0，所以 d_error = -current_qvel

        # 计算自适应的比例增益和微分增益
        adaptive_Kp = Kp0 + lambda_param * np.abs(error)
        adaptive_Kd = Kd0 + lambda_param * np.abs(d_error)

        torque = adaptive_Kp * error + adaptive_Kd * d_error

全代码为：

import mujoco
import mujoco.viewer
import numpy as np
import time

model = mujoco.MjModel.from_xml_path("/home/xw9527/.mujoco/mujoco200/model/FrankaEmikaPanda/urdf/FrankaEmikaPanda.xml") 
data = mujoco.MjData(model)

pi = 3.1415926
Kp0 = np.array([1000, 800, 500, 300, 50, 80, 2.5])  
Kd0 = np.array([20, 10, 10, 10, 0.5, 0.5, 0.1])  
lambda_param = np.array([0.1, 0.1, 0.1, 0.05, 0.001, 0.01, 0.0005])  

desired_qpos_start = np.array([0, 0, 0, 0, 0, 0, 0])  

desired_qpos_end = np.array([0, pi/4, 0, -pi/2, 0, 3*pi/4, 0])  

with mujoco.viewer.launch_passive(model, data) as viewer:
    last_qvel = np.zeros(7) 
    start_time = time.time()  

    while viewer.is_running():
        current_time = time.time() - start_time
        
        if current_time < 6:
            desired_qpos = desired_qpos_start
        else:
            transition_time = min(current_time - 6, 6)  
            alpha = transition_time / 6  
            desired_qpos = (1 - alpha) * desired_qpos_start + alpha * desired_qpos_end

        current_qpos = data.qpos[:7]  
        current_qvel = data.qvel[:7]
        
        error = desired_qpos - current_qpos
        d_error = -current_qvel 

        adaptive_Kp = Kp0 + lambda_param * np.abs(error)
        adaptive_Kd = Kd0 + lambda_param * np.abs(d_error)

        torque = adaptive_Kp * error + adaptive_Kd * d_error
        data.ctrl[:7] = torque 

        mujoco.mj_step(model, data)

        viewer.sync()

        # 200Hz
        time.sleep(max(0, 0.005 - (time.time() - current_time)))

控制结果基本和滑模以及其他算法一致了，由于控制精度的提高必须通过比较控制器的跟踪误差才能反映出控制精度的强弱了，因此此处不再给出仿真的预览图，有兴趣的可以通过自己运行此代码观察，最好是利用matplot函数输出数据列出图比较。

总结

文章采用多种基础控制器在mujoco当中控制机械臂简单运动，算法设计目标是可以用就行，有较高重复性和不严谨性，仅供参考。