GAN的Loss的比较研究——传统GAN的Loss的理解

参考文献：

https://blog.csdn.net/StreamRock/article/details/81096105

https://www.cnblogs.com/kai-nutshell/p/12968454.html

参考文献1中给出对于loss_D的解释，鄙人表示很不错，但是对于Loss_G的解释太过于笼统，没有给出具体的解释。本文将继续解释

GAN里面有两个Loss：Loss_D（判别网络损失函数）、Loss_G（生成网络损失函数）。
Loss_D只有两个分类，Real image判为1，Fake image（由G生成）判为0，因而可以用二进制交叉熵（BCELoss）来实现Loss_D。

熵

熵（Entropy），是描述一个随机信号源的信息量的指标，为叙述方便，采用离散信号源。设信号源(S)可以发送N个符号{S1​,S2​,...,SN​}，符号Si​出现的概率为Pi​，则该信号源所发送一个符号的平均信息量，即熵为：

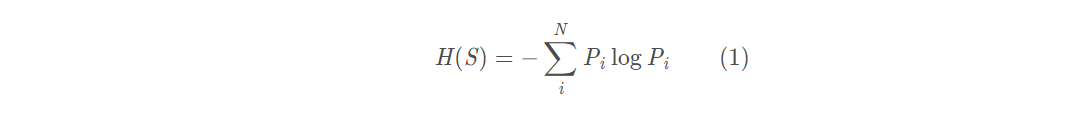
于是，熵就可以看成是一个概率的信息度量，于是从信息论过渡到概率度量上。对于连续概率分布，使用概率密度p(x)代替（1）式中的概率Pi​，有：

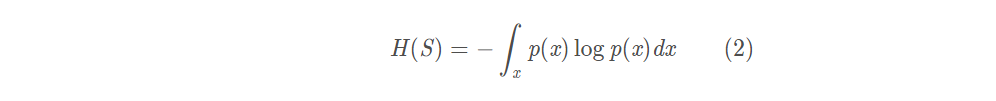
交叉熵（Cross Entropy）

交叉熵（Cross Entropy）是描述两个随机分布（P、Q）差异的一个指标，其定义如下：

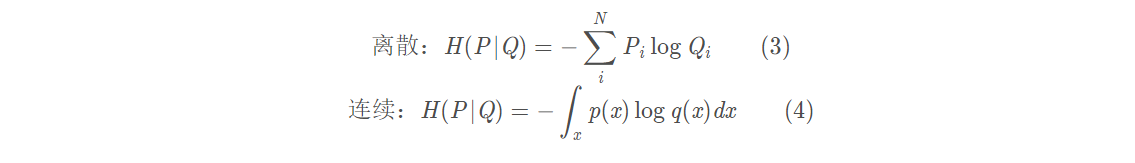
P、Q的顺序不能互换。当P与Q相同时，交叉熵取最小值，此时计算的是P（或Q）的熵。

二进制交叉熵（Binary Cross Entropy）

二进制交叉熵（Binary Cross Entropy）是指随机分布P、Q是一个二进制分布，即P和Q只有两个状态0-1。令p为P的状态1的概率，则1-p是P的状态0的概率，同理，令q为Q的状态1的概率，1-q为Q的状态0的概率，则P、Q的交叉熵为(只列离散方程，连续情况也一样)：

注意这里说的是二进制交叉熵，其实就是对于公式3（离散型）中的N=2，i = {1,2}。

GAN

Discriminator的Loss

在GAN中，判别器（Discriminator）的输出与ground-truth（它的取值只有0-1）被看作是概率。交叉熵就是用来衡量这两个概率之间差异的指标：p反映的是ground-truth认为来自real的概率，用L表示（ground truth label）此分布，它只取两个值100%和0%，即1和0；q反映的是Discriminator认为的来自real的概率，用D（Discriminator prediction）表示此分布，它的取值是[0,1]。

一个样本（1幅图片）x，假如来自real，p则为1，q为D(xr​)，其交叉熵输出是：

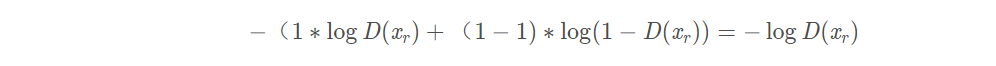
对应的代码段：

D_real_loss = BCE_loss(D_result, y_real_)

假如来自fake，p则为0，q为D(xf​),其交叉熵为：

对应代码段：

D_fake_loss = BCE_loss(D_result, y_fake_)

上面说仅仅是针对一个样本，但是代码段却是针对的整个样本集。所以下面要介绍关于数据集的交叉熵

D的目标是让Pd​接近理想概率分布iPi​（Pi​分布是：real sample输入时，概率输出为1；fake sample输入时，概率输出为0）。因此交叉熵越小越好，即：

 

插播解释：

通过上面的“插播解释”，我们就会很容易的解释和理解下面的公式和代码的对应关系：

以下是一段来自https://github.com/znxlwm/pytorch-MNIST-CelebA-GAN-DCGAN/blob/master/pytorch_MNIST_DCGAN.py的代码：

y_real_ = torch.ones(mini_batch)    # ground-truth 全为1
y_fake_ = torch.zeros(mini_batch)   # 全为0

x_, y_real_, y_fake_ = Variable(x_.cuda()), Variable(y_real_.cuda()), Variable(y_fake_.cuda())
D_result = D(x_).squeeze()
D_real_loss = BCE_loss(D_result, y_real_)  # 应用BCELoss

z_ = torch.randn((mini_batch, 100)).view(-1, 100, 1, 1)
z_ = Variable(z_.cuda())
G_result = G(z_)

D_result = D(G_result).squeeze()
D_fake_loss = BCE_loss(D_result, y_fake_)  # 应用BCELoss
D_fake_score = D_result.data.mean()

D_train_loss = D_real_loss + D_fake_loss # 实现上述公式7

Generator的Loss

也就是说我们需要优化的是-log(D(G(z))。

在生成器中，是为了可以更好的模拟出真实的图片，所以要让生成的图片更加真实。 更加接近于1，所以这里是Df和1的交叉熵。

G要达到以假乱真的地步，所以D对G生成的图像判别为1的概率越高越好，所以对应p = 1——>(y_real_),q = log(D(G(z)))——>(D_result )，进行二进制交叉熵的计算。

对应的代码段:

G_train_loss = BCE_loss(D_result, y_real_) # y_real_全部为1
G_train_loss.backward()
G_optimizer.step()