拉格朗日松弛求解问题

最新推荐文章于 2023-12-14 10:32:31 发布

CodeSavior

最新推荐文章于 2023-12-14 10:32:31 发布

阅读量1.9k

点赞数

分类专栏：算法文章标签：优化

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/CodeSavior/article/details/126392991

版权

算法专栏收录该内容

3 篇文章 2 订阅

订阅专栏

1、概述

直观上拉格朗日松弛方法就是将约束中难解的部分变为目标函数中的一部分，扩大搜索的范围。

拉格朗日松弛方法不仅能够求解非线性规划问题还能求解整数规划问题。

整数规划问题求解方法

benders decomposition
dantzg-wolfe decompostion
lagrangian decompostion

拉格朗日松弛之后得到的问题下界优与等于直接将0，1整数变量松弛为0到1连续变量的下界

拉格朗日松弛之后我们会得到拉格朗日乘子，拉格朗日乘子反映了对偶的信息。

拉格朗日送至可以将约束中耦合的变量分解，转换成独立的子问题，简化原来的问题。

对于拉格朗日松弛后的问题我们需要做两方面内容

第一是求解子问题，第二是拉尔朗日乘子的更新

子问题一般不是NP难的，一般是规模比较小的可以直接求解的，否则证明子问题分解的还不够彻底。一般子问题可以通过求解器直接求解，或者采用动态规划，线性规划等手段求解。

拉格朗日乘子的更新本质上是求解对偶问题，对偶问题是一个非光滑的凸优化问题，可以利用次梯度算法来更新拉格朗日乘子

拉格朗日对偶有一下几个良好的性质

无论元问题是否为凸，对偶问题都是凸优化问题
对偶问题至少给出了原问题最优解的下界
在满足一定条件下，对偶问题和原问题的解完全等价
对偶问题通常容易求解

拉格朗日对偶的目标就是将带有约束的优化问题转化为不带约束或者约束简单的凸优化问题

2、拉格朗日函数、拉格朗日对偶函数以及拉格朗日对偶问题

2.1、原问题

对于原问题

$P_1=\min f(x)\\ s.t. g_i(x)\leqslant 0,i=1,2\cdots m\\h_i(x)=0, i=1,2\cdots p$

其中约束是凸集，但是目标函数不一定是凸函数

2.2、拉格朗日函数

拉格朗日函数：是将约束变为目标函数中的一部分，是一个关于 $x, \lambda ,v$ 的函数

$L(x,\lambda ,v)=f(x)+\sum_{i=1}^{m}\lambda _i g_i(x)+\sum_{i=1}^{p}v_i h_i(x)$

x是原问题的自变量， $\lambda$ ，v是拉格朗日乘子是标量。

介绍完拉格朗日函数，它和原问题有什么关系呢？？

2.3、拉格朗日函数与原问题

直接抛出结论：最大最小拉格朗日函数和原问题是等价的

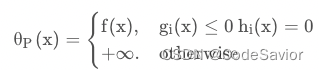
我们分开来求，首先是 $\theta_P(x)=\underset{\lambda ,v}{\max} L(x,\lambda ,v)$

接下来我们要求 $\underset{x}{\min }\theta_P(x)$ ，它的解和原问题的解相同。

如前文描述的那样，由于目标函数不一定是凸函数，所以优化问题 $\theta_P(x)$ 是难解的，所以自然想到，摆脱自变量x，将问题转化为好解的凸问题，拉格朗日对偶函数由此诞生。

2.4、拉格朗日对偶函数

$\theta_D(\lambda ,v)=\underset{x}{\min} L(x,\lambda ,v)$

我们称上面的式子是拉格朗日对偶函数，是对变量 $\lambda,v$ 求函数L的最小值的问题，

而拉格朗日对偶函数是凹问题，极大化一个凹问题是凸问题，所以我们构造了如下问题

$\underset{\lambda,v}{\max } \theta_D(\lambda ,v)$

我们定义如上问题为，拉格朗日对偶问题

假设拉格朗日对偶问题的局部最优解为d*，原问题f(x)的最优解为p*

可以证明 $d*\leqslant p*$

参考的文章

拉格朗日对偶详解_左痕生的博客-CSDN博客_拉格朗日对偶
 拉格朗日对偶性详解（手推笔记）_见见大魔王的博客-CSDN博客_拉格朗日对偶性

关注

0
点赞
踩
10

收藏

觉得还不错? 一键收藏
1
评论
拉格朗日松弛求解问题

拉格朗日乘子法求解优化问题
复制链接

扫一扫

专栏目录

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。