机器人控制范式：从模型优化到策略学习的底层逻辑

在人形机器人技术日新月异的今天，我们有必要暂时从令人惊叹的演示视频和高度堆叠的算法中抽离，回归工程师的视角，审视驱动这些复杂系统的底层——控制范式。

本文将对两大阵营进行一次技术解构：

1. 基于模型的最优控制： 以MPC+WBC为代表，将控制问题定义为一个可解析的约束优化问题。
2. 数据驱动的策略学习： 以IL和RL为代表，将控制问题定义为一个通过数据学习策略函数（Policy）的泛化问题。

我们的讨论将聚焦于“为什么”而非“好不好”，旨在揭示范式背后的核心假设及其带来的必然结果。

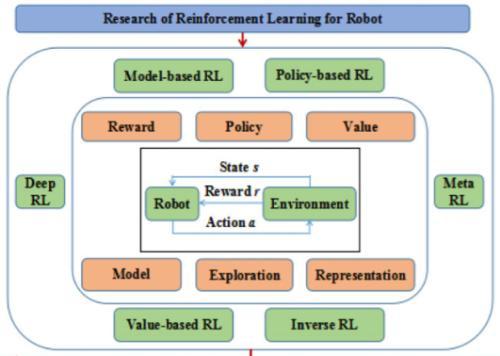
一、模型为纲：基于显式优化的MPC+WBC范式

该范式的核心信仰是：如果拥有一个足够精确的世界模型，最优控制问题就可以被形式化地求解。

底层问题定义：约束轨迹优化

其数学本质是在每一个离散时间步 k，求解一个具有以下形式的有限时域最优控制问题（OCP）：

min_{u_k, ..., u_{k+N-1}}  Σ_{i=k}^{k+N-1} l(x_i, u_i) + m(x_{k+N})
s.t.
    x_{i+1} = f(x_i, u_i)      // 系统动力学模型
    h(x_i, u_i) <= 0         // 路径约束 (如关节限位)
    g(x_i) <= 0              // 状态约束 (如ZMP稳定域)

• MPC (Model Predictive Control) 的职责是求解这个OCP。它利用系统动力学模型 f(x, u) 向前“预测”N步，找到一个使总代价（cost）最小的控制序列 U = {u_k, ..., u_{k+N-1}}。关键在于，它只执行序列的第一个动作 u_k，然后在下一时刻 k+1 接收新的状态 x_{k+1}，重新进行一次完整的滚动优化。这是一种在线的、反复重规划的策略。

• WBC (Whole-Body Control) 则通常作为MPC的下游任务执行器。它将MPC给出的高层运动学目标（如质心加速度、末端执行器姿态）转化为全身关节力矩。WBC本身也是一个优化问题（通常是二次规划QP），但它更关注瞬时动力学 τ = M(q)q̈ + C(q, q̇) + G(q) 和各类硬约束（接触力、摩擦锥、力矩限制），负责将“规划”落地为“物理执行”。

范式局限的根源：模型保真度

此范式的全部效能，都锚定在动力学模型 f(x, u) 和各类约束模型的准确性上。任何未建模的动力学效应（如柔性、驱动器延迟、复杂的接触物理）或环境参数失配（如地面摩擦系数、负载物体的惯量），都会直接导致优化问题的解偏离真实世界的最优，甚至导致系统失稳。其瓶颈在于为复杂、非结构化的现实世界建立一个完美可微的高保真模型，这在工程上是极其困难甚至不现实的。

二、数据为师：策略学习范式的兴起

策略学习范式转换了思路：与其尝试精确建模整个世界，不如直接学习一个从“观察”到“行动”的映射函数，即策略 π(a|s)。

澄清边界：监督学习 (SL) vs. 模仿学习 (IL)

在进入IL和RL之前，必须严格区分监督学习与模仿学习在控制领域的本质差异。

• 监督学习 (Supervised Learning)：其核心是学习一个静态映射 f: X → Y。其训练数据 {(x_i, y_i)} 通常被假设为独立同分布 (I.I.D.)。预测 y_i = f(x_i) 的行为不会对下一个输入 x_{i+1} 产生影响。这使得SL非常适合图像分类、语音识别等任务，但在闭环控制中存在根本性缺陷。

• 模仿学习 (Imitation Learning)：其目标是学习一个策略 π: S → A（从状态空间到动作空间）。它的训练数据是序列数据 τ = {s_0, a_0, s_1, a_1, ...}，其中 s_{t+1} 是由 (s_t, a_t) 决定的。数据之间存在时序依赖，不满足I.I.D.假设。IL要解决的是一个序贯决策问题 (Sequential Decision-Making Problem)，这才是控制问题的本质。简单地将控制看作“在每个状态下做一次分类/回归”，是SL对控制问题的误用。

模仿学习 (IL)：从专家范例中归纳策略

底层问题定义：以监督学习为工具，解决序贯决策问题

最基础的IL算法，行为克隆 (Behavioral Cloning, BC)，形式上看起来极像监督学习。它收集专家演示数据集 D = {(s_i, a_i)}，然后通过最小化一个监督损失（如MSE）来训练策略网络 π_θ：

L(θ) = E_{(s,a)∼D} [ ||π_θ(s) - a||^2 ]

尽管工具是SL，但其意图是学习一个能在闭环中运行的策略。这直接引出了IL的核心挑战：

核心挑战：分布偏移 (Covariate Shift / Distribution Mismatch)

1. 问题根源：BC训练的策略 π_θ 是在专家访问过的状态分布 p_expert(s) 上进行优化的。然而，由于策略网络 π_θ 不可能完美复刻专家策略 π*，在实际执行中，它会犯下微小的错误。这个错误会引导智能体进入一个新的状态 s'，而这个状态在专家数据集 D 中出现的概率极低（即 p_expert(s') ≈ 0）。
2. 恶性循环：在这些分布外 (Out-of-Distribution) 的状态上，π_θ 的行为是未定义的，很可能输出一个更糟糕的动作，导致智能体进一步偏离专家轨迹。这个过程形成误差累积，最终导致任务失败。

解决方案示例：DAgger (Dataset Aggregation)

DAgger是解决分布偏移的经典在线IL算法。其思路是让策略在训练中“见到”自己会犯错的状态：

1. 初始阶段：用专家数据 D 训练一个初始策略 π_1。
2. 迭代过程 (for i = 1, 2, …):
   a. 执行：用当前策略 π_i 在环境中执行，收集其访问的状态轨迹 {s_t}。
   b. 查询：对于收集到的每个状态 s_t，向在线的专家查询此时应采取的正确动作 a_t* = π*(s_t)。
   c. 聚合：将新收集到的数据对 {(s_t, a_t*)} 聚合到原始数据集 D 中。
   d. 再训练：用聚合后的新数据集 D 重新训练策略，得到 π_{i+1}。

DAgger的本质是将问题从“模仿专家做什么”转变为“学习如何在自己会到达的状态下，做出专家会做的决策”，从而有效缓解了分布偏移，典型的论文例如OmniH2O，在里面大量讨论了Dagger加入后产生的影响。

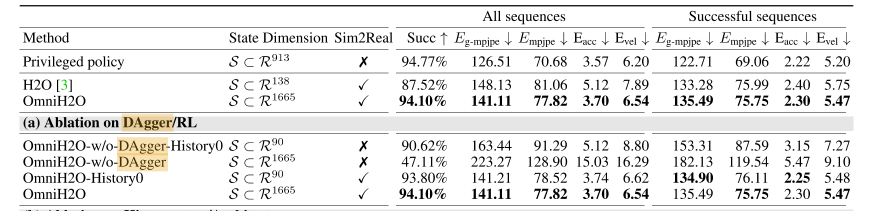
强化学习 (RL)：从标量奖励中发现策略

底层问题定义：最大化期望累积奖励的马尔可夫决策过程 (MDP)

RL彻底抛弃了专家演示，它的唯一监督信号是一个人为设计的标量奖励函数 r(s, a)。RL将控制问题建模为一个MDP，其目标是寻找一个策略 π，以最大化折扣累积奖励的期望：

J(π) = E_{τ∼π} [ Σ_{t=0}^∞ γ^t * r(s_t, a_t) ]

• 学习信号的差异：这是RL与IL的根本区别。IL的监督信号是高维、稠密的专家动作向量 a*，它直接告诉策略“该做什么”。而RL的监督信号是低维、通常稀疏的奖励标量 r，它只告诉策略当前行为的“好坏程度”，而不提供具体修正方向。

• 探索-利用困境 (Exploration-Exploitation Dilemma)：由于没有专家指引，RL智能体必须通过探索 (Exploration) 来尝试新的动作以发现潜在的高奖励区域，同时也要利用 (Exploitation) 已知的最佳策略来获取奖励。平衡二者是RL算法设计的核心。

RL的强大之处在于，它不被专家知识所束缚，有可能通过探索发现超越人类直觉的、性能更高的策略。其代价是巨大的样本复杂度和对奖励函数设计的敏感性。

核心挑战：奖励函数设计的难度和样本效率的低下
奖励函数的设计稍有不慎，智能体就可能“钻空子”，学会以投机取巧的方式最大化奖励，而非完成任务本身。此外，RL需要天文数字般的交互数据才能学到有效策略，这使得训练过程高度依赖于高速、高保真的模拟环境，从而还产生了业界一直致力于攻克的sim2real难题。

四、范式解构与比较

下表从技术底层对三大范式进行归纳：

范式	核心问题公式化	知识/监督来源 (“Oracle”)	技术优势	技术瓶颈
MPC+WBC	有限时域约束优化	精确的、可微的系统动力学模型 f(x, u)	在模型可信域内，提供最优性、安全性和可解释性保证。	对模型失配极其敏感；高维非凸优化求解耗时。
模仿学习 (IL)	序贯决策问题，用监督学习求解	专家策略 π* 提供的状态-动作对 (s, a*)	无需设计奖励函数；可学习人类的复杂、隐式技能；样本效率相对较高。	性能上限受限于专家水平；核心挑战是分布偏移。
强化学习 (RL)	马尔可夫决策过程 (MDP)	人工设计的奖励函数 r(s, a)	能够发现超人类性能的策略；无需专家数据。	奖励函数设计困难（易导致Reward Hacking）；样本效率极低；探索成本高。

通过以上解构，我们可以清晰地看到：

• MPC+WBC 是一个在“已知世界”中追求“确定性最优”的范式。
• IL 是一个在“专家经验”中学习“行为范式”的范式。
• RL 是一个在“未知环境”中通过“试错反馈”寻找“概率性最优”的范式。

它们并非相互替代，而是针对不同问题假设的工具。未来的高级人形机器人控制系统，几乎必然是这些范式的混合体，现在的研究方向也基本在混合控制上进行探索。